| 2021年05月30日 | 更新。 |
72の法則は、資産を、一定の年利の金融商品で運用した時、資産を元値の2倍にするために必要な年数の近似値が、簡単な計算で求められる事を示す法則です。
具体的には、x%の年利(年間収益率)で複利計算をした場合、資産が2倍になる年数をy年とすると、72の法則は、yが式(1)で近似的に求まる事を示します。
余談:数学的に証明できる式(公理と定義から証明できる式)は、普通は法則とは呼ばずに定理と呼びます。よって式(1)は「72の定理」と呼ぶ方がふさわしいと思われますが、習慣的に「72の法則」と呼ぶ様です。72の法則の数学的な証明に関しては、後述します。
72の法則を用いた計算例を、以下に2つ示します。
5%の年利で運用して資産を2倍にするのに必要な年数は、x=5を式(1)に代入して、72÷5=14.4年と計算できます。
式(1)を変形すると、式(2)が得られます。
この式から、y年で資産を2倍にするのに必要な年利x%を、近似的に求められます。
例えば、10年で資産を2倍にするのに必要な年利は、式(2)にy=10を代入して、72÷10=7.2%と計算できます。
72の法則は近似式なので、計算誤差が出ます。どの程度の計算誤差が出るかについては後述します。
金融商品で運用益が出た場合には、税金がかかります。例えば債券の利子や譲渡益には20.315%の税金がかかります。(2021年5月時点) 72の法則を使って計算する場合は、税金が引かれる前の表面金利ではなく、税引き後金利で計算する必要があります。
また、金融商品の売買に手数料が必要な場合もあります。正確に計算するには、こういった費用も考慮する必要があります。
72の法則は、資産が複利計算で増えていく事を前提にしています。単利計算で増えていく場合には適用できません。
例えば、年利5%の債券に投資する場合を考えると、多くの場合、半年に1度、額面の2.5%に相当する利息が支払われます。この利息をそのまま受け取って再投資しない場合は、単利計算になりますので、72の法則の前提に合致しません。受け取った利息を年利5%の債券に再投資すると、複利計算で資産が増え、72の法則の計算の対象になります。
銀行の利息でどの程度資産が増えるかを見積もる場合は、利息が口座に入ると、その利息にもさらに利息が付きますから、複利計算になります。
収益が投資対象の状況(株式に投資した場合は投資した会社の経営状況など)により大きく変動する場合は、年間収益率を平均して式(1)のxに代入しても、資産を2倍にするのに必要な年数が正しく求まりません。
例えば、年間収益率が37.2%の(1年で資産が1.372倍になる)年と年間収益率が-22.8%の(1年で資産が0.772倍になる)年を交互に繰り返す場合を考えます。
この場合、平均的な年間収益率は37.2+(−22.8)2=7.2%となります。x=7.2を式(1)に代入すると、y=727.2=10となり、10年で資産が2倍になりそうな気がしますが、実際に10年で資産が何倍になるかを正確に計算すると、(1.372×0.772)5≒1.333倍にしかなりません。
参考:この計算例が示す様に、収益率の変動が激しい投資対象に投資をすると、平均的な年間収益率が高くても、トータルのリターンが意外と小さくなります。
一方で、毎年確実に7.2%の収益が出る金融商品に投資すれば、10年で1.07210≒2.004倍と、72の法則で計算した通り、約2倍に資産が増えます。
この様に、72の法則は、収益率が大きく変動する金融商品に関する試算には向きません。
72の法則が主張する式(1)は近似式ですので、近似誤差が出ます。この章では、式(1)でどの程度の計算誤差が発生するのかや、どのような条件の場合に、計算誤差が少なくなるかについて考えます。
年利x%でy年運用して資産が2倍になる場合、正しくは式(3)が成立します。
式(3)を変形すると、式(4)の様に、yを与えるとxが求まる計算式が得られます。
この式(4)は、72の法則とは違い、厳密に成立する式です。
式(4)を使えば72の法則よりも正確に計算できるのですが、式(4)を計算するには、関数電卓(あるいはExcelの様な関数の計算できるパソコンソフト)と、若干の数学的素養が必要です。(写真1参照)
一方で、72の法則を使えば、計算結果には少し誤差が含まれるものの、数学の知識のない人でも普通の電卓を使って(場合によっては暗算で)計算をする事ができます。

式(4)にy=10を代入した式を関数電卓に打ち込んで、10年で資産を2倍にするのに必要な年数を計算しています。
y年運用して資産を2倍に増やすのに必要な年利x%を式(4)および72の法則(式(2))で求め、計算結果をまとめたのが表1です。
| 年数 [年] |
式(4)で厳密に 求めた年利 [%] |
72の法則で近似的 に求めた年利 [%] |
|---|---|---|
| 1 | 100.0 | 72.00 |
| 2 | 41.42 | 36.00 |
| 3 | 25.99 | 24.00 |
| 4 | 18.92 | 18.00 |
| 5 | 14.87 | 14.40 |
| 6 | 12.25 | 12.00 |
| 7 | 10.41 | 10.29 |
| 8 | 9.051 | 9.000 |
| 9 | 8.006 | 8.000 |
| 10 | 7.177 | 7.200 |
| 12 | 5.946 | 6.000 |
| 15 | 4.729 | 4.800 |
| 20 | 3.526 | 3.600 |
| 50 | 1.396 | 1.440 |
| 100 | 0.6956 | 0.7200 |
| 200 | 0.3472 | 0.3600 |
| 500 | 0.1387 | 0.1440 |
| 1000 | 0.06934 | 0.07200 |
9年間運用して資産を2倍にするのに必要な年利は、正しくは8.006%で、72の法則から求めると丁度8%になる事が、表1より分かります。この様に、運用年数が9年付近、あるいは年利が8%付近の場合は、72の法則が、ほぼ正確に成り立ちます。
資産運用年数が9年より短くなると、72の法則で計算したのでは、必要な金利を実際より低く見積もります。運用年数が1年の場合は、正しい年利が100%なのに対し、72の法則では72%と、28%も低く見積もってしまいます。
資産運用年数が9年より長くなると、72の法則で計算したのでは、必要な金利を実際より高く見積もります。ただし、運用年数がどんどん長くなっていっても、それに応じて金利の計算誤差がどんどん増える訳ではなく、計算誤差は4%以内に収まります。(例えば1000年で資産を2倍にする場合を考えると、(0.07200÷0.06934−1)×100=3.84%の計算誤差になります)
以上の様に、72の法則では、資産運用年数が9年程度、あるいは年利が8%程度の場合に、一番計算誤差が少なくなります。運用年数が極端に短かったり、年利が極端に高い場合は計算誤差がかなり大きくなります。(運用年数が0年に近づくと、計算誤差が上限なく増えていきます)
逆に運用年数が極端に長かったり、年利が極端に低い場合にも誤差が出ますが、その時の計算誤差は4%以内に収まります。
運用年数が極端に長かったり、年利が極端に低い場合は、72の法則を使うより、式(5)に示す69の法則を使う方が、より正確に答えを求められます。
近年は、慢性的な金融緩和により、銀行で定期預金をしても、金利が0.1%を下回る状態が続いています。この様な状態で金利と資産を2倍にするのに必要な年数の関係を計算するには、72の法則より69の法則を使う方が、より正確な答えが出ます。
資産を2倍にするのに必要な運用年数と年利の関係を、式(4)により厳密に求めた解と、式(2)の72の法則により近似的に求めた解と、式(5)の69の法則により近似的に求めた解の3つについてグラフ化したものを、図1に示します。
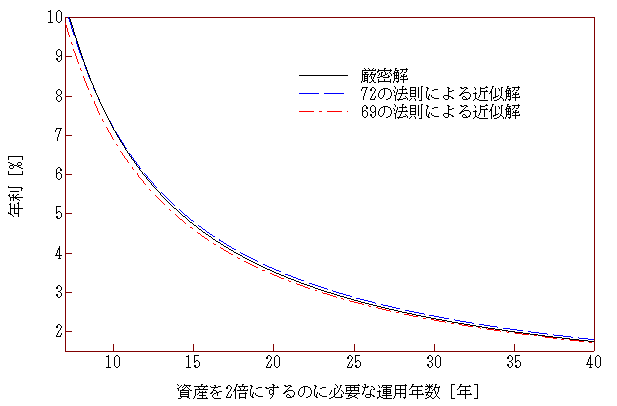
グラフがちょっと見づらいですが、年利が下がって運用年数が長くなっている領域(グラフの右下の領域)では、72の法則より69の法則の方が精度よく近似できており、年利が8%で運用年数が9年程度の領域(グラフの左上の領域)では、69の法則より72の法則の方が精度よく近似出来ています。
図1のグラフが少し見づらかったので、横軸を運用年数、縦軸を72の法則および69の法則で求めた年利の近似誤差にして、それらの関係をグラフ化したのが図2です。
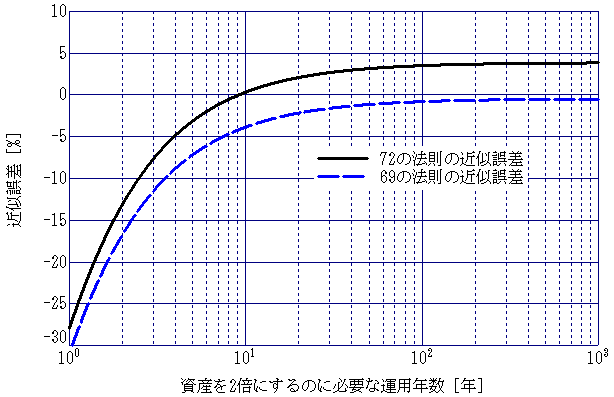
図2において、近似誤差は100×近似式で求めた年利厳密に求めた年利−1[%]で求めています。近似誤差が大きいほど年利を多く見積もっている事になり、近似誤差が0%の時に正しい計算が出来ている事になります。
運用年数が非常に長い領域(グラフの右側)では、72の法則では3.9%程度、年利を高く見積もります。一方で、69の法則では0.5%程度年利を低く見積もりますが、72の法則よりも精度よく年利が計算できます。
参考:後述するように、69.315の法則にすれば、運用年数が非常に長い領域で、正確に年利の計算ができます。
運用年数が非常に短い領域(グラフの左側)では、72の法則、69の法則共に、年利を大幅に低く見積もります。ただし、72の法則の方が、誤差(の絶対値)がやや小さくなります。
運用年数が約9年の時に、72の法則の近似誤差が0になる事が、図2からも確認できます。
式(4)を基に、運用年数を入力すると、資産を2倍にするのに必要な年利を計算するツールを作りました。
画面1が、そのツールです。画面をクリック(またはタップ)して、運用年数を半角数字で入力後、ENTERキーを押すと、年利の計算結果を表示します。なお、運用年数は、正の数でなければなりませんが、整数でなくても入力できます。
式(3)をyについて解くと式(6)が得られます。
式(6)に基づいて、年利を入力すると、資産を2倍にするのに必要な運用年数を計算するツールを作りました。
画面2が、そのツールです。画面をクリック(またはタップ)して、年利を半角数字で入力後、ENTERキーを押すと、運用年数の計算結果を表示します。なお、年利は、正の数でなければなりませんが、整数でなくても入力できます。
パーセント単位で表した年利を半角数字で入力してENTERキーを押すと、その年利で資産を2倍にするのに必要な運用年数を計算します。式(6)に基づく厳密な年利だけでなく、72の法則や69の法則で近似計算した年利も表示します。
例えば年利に3.5%を入力すると、資産を2倍にするのに約20.1年かかると表示されるはずです。この計算結果は、表1から20年で資産を2倍にするのに必要な年利が3.526%と求まる事と、符合します。
年利1%で計算すると、資産を2倍にするのに約69.7年かかる事が分かります。1%の利率では、資産を2倍にするだけで、人生の大半を費やしてしまいます。銀行の定期預金が0.1%を下回る様な状況では、銀行の預金で運用した場合に、一生をかけてもほとんど資産が増えない事が分かります。
参考:画面2のプログラムで、年利の代わりに物価上昇率を入力すると、物価が2倍になるのにかかる年数が計算できます。試しに2%を入力して計算すると、約35年で物価が2倍になる事が分かります。日本銀行が目標にしている物価上昇率が2%なのですが、35年で物価が2倍になる様な物価上昇率を目指している事が分かります。ただし、物価上昇率2%を「目指して」いるだけで、長年全く達成されていません。
x%の年利でa年間資産を運用した時に、資産が元本のb倍になったとすると、式(7)が成立します。
この式をaについて解くと、式(8)の様になります。
式(8)に基づいて、年利と資産の倍率とを入力すると、資産を入力された倍率に増やすのに必要な運用年数を計算するツールを作りました。例えば5%の年利で資産運用すると仮定して、資産を7倍にするために必要な運用年数を計算する場合に使います。(この問題の答えは約39.9年)
画面3が、そのツールです。画面をクリック(またはタップ)して、年利と資産の倍率(資産を何倍にしたいか)を半角数字で入力後、ENTERキーを押すと、運用年数の計算結果を表示します。なお、年利には正の数を入力してください。また資産の倍率には、1以上の数を入力してください。
パーセント単位で表した年利と資産の倍率(資産を何倍にしたいか)を半角数字で入力してENTERキーを押おすと、必要な運用年数を計算します。
計算は式(8)に基づいて行っています。
72の法則の式を見ると、72という数字がどこから出てくるのか不思議に思われるのではないでしょうか?この章では、72という数字の出どころを含めて、72の法則の理論的な背景について話します。
x%の年利で運用して、資産を2倍にするのにかかる運用年数をy年とすると、yは式(6)で得られます。
式(6)には自然対数(ln)が出てきますが、自然対数に関しては、式(9)と式(10)が成立します。
式(9)と式(10)より、lnxをx=1の近傍で1次近似(直線近似)をする事により、xが十分小さいときに次の様な近似式が成り立つ事が分かります。
ln 2≒0.69315である事と式(11)から、式(6)は、xが十分小さい時に、式(12)の様に近似できます。
この式は、69の法則を表す式(5)に、ほぼ一致します。つまり、69の法則の69とは、100 ln 2の事だったのです。正確には69.315の法則なのですが、キリが悪いので69の法則と呼ばれています。
年利がほぼ0%の領域では69.315の法則が成り立ちますが、年利が大きくなると、69.315の法則では運用年数を短めに見積もってしまいます。そこで、69を少し大きめに修正しなければなりません。もし72に修正すると、前述の通り年利が約8%(運用期間が約9年)の所で近似誤差が0になります。
別に70の法則(年利が約2%の時に計算誤差がなくなる)でも71の法則(年利が約4.9%の時に計算誤差がなくなる)でもいいと思うのですが、インターネットを色々調べてみたところ、72には約数が多く(72を素因数分解すると23×32)、色々な金利、色々な運用年数について、暗算で試算できるので便利だというのが、72が選ばれた理由ではないかという説があるみたいです。
