
| 2015年09月01日 | 公開。 |
ここからは、製作した電卓の使い方や、使う上での注意点などを書きます。
今回製作した電卓は、6桁電卓です。市販されている電卓は通常8桁電卓で、関数電卓や金融電卓だとさらに多い桁数を扱えますから、今回製作した電卓は、それらより扱える桁数が少ないことになります。6桁電卓になった理由については後述します。
製作した電卓についているボタンの意味や働きを、表4に示します。
| ボタン | 意味や働き |
|---|---|
| 0~9 | 数字を入力する |
| . | 小数点を入力する |
| +/- | 入力中の数の正負を反転させる |
| ÷ | 割り算を行う |
| × | 掛け算を行う |
| − | 引き算を行う |
| + | 足し算を行う |
| = | 最終的な計算結果を得る |
| C | 入力した内容を全て破棄し、計算を最初からやり直す (エラーが出た時の復帰にも使う) |
| CE | 現在入力中の数字を入力し直す |
| ← | 現在入力中の数字の最後の桁を入力し直す |
今回製作した電卓の使い方は、市販されている電卓とほぼ同じです。例えば、(1.23+4.56)×7.8の計算をしたい場合は、1.23+4.56×7.8=の順にボタンを押せばOKです。(関数電卓と違い、足し算より掛け算を優先して計算するという考え方がないので、括弧を無視して入力してよい)
ただ、市販の電卓と違うのは、液晶が2行ある事を利用して、上の行に履歴表示が出ることです。この履歴表示というのは、最後に入力した数(または最後の計算結果)と、最後に入力した四則演算ボタンの種類を表示する機能の事です。
言葉で説明したのでは、解りにくいので、写真を示しながら説明します。
電卓を起動した直後(あるいはCキーを押した直後)では、電卓は写真11の様に、0を表示します。
ここで、1.23と入力すると、写真12の様に、1.23と表示されます。
さらに+ボタンを押すと、写真13の様に、1行目に1.23 +と表示され、2行目に0と表示されます。この1行目の1.23 +が履歴表示です。また、市販の電卓では+ボタンを押した直後は1.23と表示さますが、この電卓では2行目に0と表示される点にも注意してください。
次に4.56を入力すると、写真14の様に、1行目の履歴表示は変化せず、2行目が4.56の表示になります。
ここで×ボタンを押すと、写真15の様に、履歴表示が5.79 *になります。この5.79という数字は、1.23+4.56の計算結果です。また、×という文字は、ASCIIコードにはありませんので、*で代用しています。(同様に、割り算の場合は、÷という文字を/で代用する)
さらに7.8=と入力すると、写真16の様に、最終的な計算結果の45.162が表示されます。
続けて別の計算をしたい場合は、Cキーを押してから計算してください。
数字を入力し間違えた場合は、CEボタンを押すと、数字を入力しなおす事ができます。
例えば、123+456と入力しようと思い、123+457と入力してしまった場合、画面表示は写真17の様になっているはずです。
ここでCEボタンを押すと写真18の様になり、間違えた数字457を入力し直す事ができます。
ここで456と入力すると、写真19の様に、訂正できます。
しかし、CEボタンを使ったのでは、456の3桁の数字を全て打ちなおさなければなりません。訂正するのが最後の桁だけの場合は、←ボタンを使うと便利です。
写真17の状態で←ボタンを押すと、写真20の様になります。
ここで、最後の桁の6を押すと、写真21の様に訂正できます。
元々、最低限の機能の電卓を作るには1ページの図1に示したボタンがあれば十分だと見積もったのですが、19個のボタンだとキリが悪いので、20個に増やしました。この際1個余分に追加されたボタンを、1桁訂正用の←ボタンに割り当てました。
計算をすると、エラーが発生する事があります。
例えば、987654+123456=と入力すると、オーバーフローエラー(取り扱える数字の範囲を超えたエラー)になります。この電卓は6桁電卓なので、取り扱える数字の範囲は-999999~999999までです。しかしながら、先ほどの足し算の計算結果は、この範囲を超えてしまうために、エラーになるのです。エラーが発生すると写真22の様な表示になります。
また、何かの数字を0で割ると、エラーになります。例えば1÷0=と入力するとエラーになり、この場合も写真22の様な表示になります。
エラーが出た際は、Cボタンを押すと、エラー表示が解除され、次の計算ができるようになります。
今回製作した電卓が6桁電卓になったのは、演算にfloat型(単精度浮動小数点数)を使用したためです。float型は精度が10進数換算で6~7桁程度になります。そこで、ほぼ上限の6桁の電卓としました。
double型(倍精度浮動小数点数)の演算ができれば15桁の精度が出るのですが、残念ながらArduinoではdouble型を扱えません。(正確に言うとdouble型の変数を宣言できるが、float型と同じ精度になる)
また、入力した10進数を2進数に変換してから計算を行った後、計算結果を10進数に変換し直して結果を表示する仕組みになっているため、10進数と2進数の変換の際に丸め誤差が発生します。
普段コンピュータを使う際に、この丸め誤差の事を意識する事は少ないかもしれませんが、実際にはコンピュータで数値計算をする多くの局面(例えばExcelのワークシートを使う場合など)で、この誤差は発生しています。
例として、Excel 2013で(123.45-123.44)×100-1の計算をする場合を考えて見ましょう。この式は暗算で計算できますが、正解は0になります。しかしながら、実際にExcelで計算させると、次に示す様に、答えは0にはなりません。
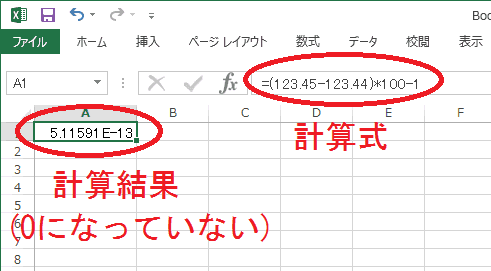
注:5.11591E-13というのは、5.11591×10−13、別の書き方をすれば0.000000000000511591を意味する。
Excelも、今回製作した電卓と同様、計算する際にいったん数を2進数に変換するのですが、変換の際に生じる丸め誤差が原因で、図18の様な計算誤差が生じたのです。
この丸め誤差は、有限の桁数の10進数でも、2進数に変換すると無限の桁数の小数になることがあり、その場合に変換を有限の桁数で打ち切ると、発生します。例えば、10進数の0.1は、2進数に変換すると、0.000110011001100110011…という無限に続く小数(循環小数)になります。これを、コンピュータが扱えるように、有限の桁で打ち切ると、そこで丸め誤差という誤差が発生するのです。
逆に有限の桁数の2進数を10進数に変換すると、必ず有限の桁数の10進数になるのですが、とても桁数が多くなる事があり、その場合にも丸め誤差が発生することがあります。例えば、2進数の0.000000001は、10進数に変換すると、0.001953125となります。通常の8桁電卓では、小数点以下8桁目を四捨五入あるいは切り捨てして表示するしかありませんので、0.0019531という表示になってしまいます。
話が脱線するので、この現象については、これ以上深くは説明しませんが、興味がある方は、次のサイトを読むと参考になると思います。
市販の電卓では一般にBCD(2進化10進数)という、本来は2進数しか扱えないコンピュータで10進数を扱う手法を使っており、10進数を2進数に変換することなく計算を行います。よって、図18で示した様な誤差は生じません。
今回製作した電卓では、Excelと同様、10進数と2進数の間の変換を行っており、またExcelが倍精度で計算するのに対して、製作した電卓では単精度で計算するため、原理的には丸め誤差の影響が出やすくなっています。しかしながら、プログラム上の工夫をすることにより、丸め誤差の影響が極力表面化しないようにしてあります。
このページでは、製作した電卓の使い方や、使う上での注意点を説明しました。次のページでは、製作した電卓のスケッチの動作原理について、説明します。
 |
商品名 | I/Oピン一つで読める4X5キーパッドキット |
| 税抜き小売価格 | 2400円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X5キーパッドキットサポートページ |
 |
商品名 | Arduino用ブートローダ/スケッチライタキット |
| 税抜き小売価格 | 3000円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | Arduino用ブートローダ/スケッチライタキットサポートページ |
