| 2020年02月06日 | 更新 |
ΔΣ型のA/D変換器でA/D変換を行うと、A/D変換の際に発生するノイズ(量子化ノイズ)が高い周波数に集中して発生する現象が起こります。この様に量子化ノイズを高い周波数に集中させる操作、あるいは量子化ノイズが高い周波数に集中する現象をノイズシェーピング(noise shaping)といいます。
参考:ノイズシェーピングの事をノイズシェイピングと記す場合もあります。
ノイズシェーピングの性質を利用すると、1ビットのA/D変換結果をデジタルLPFに通し、ダウンサンプリングする事で、複数ビット(マルチビット)のA/D変換器を、等価的に構成できます。
この節では、ノイズシェーピングの原理について説明し、また、ノイズシェーピングを利用して複数ビットのA/D変換器を構成する方法について解説します。
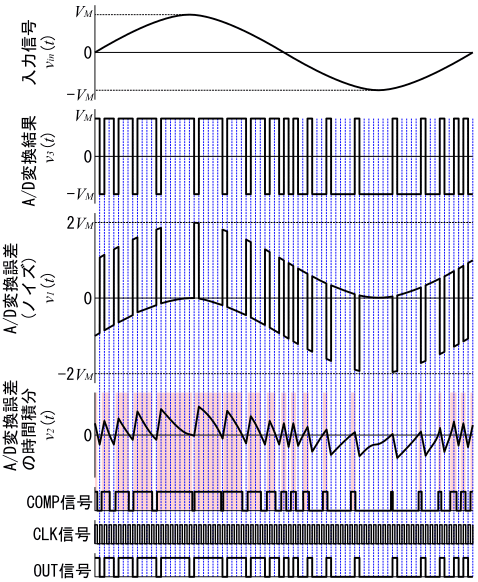
図9の1ビットA/D変換器に振幅VMの正弦波の信号を入力した場合の、回路各部の電圧波形を図25に示します。
OUT信号が、この1ビットA/D変換器の出力信号ですが、この信号をLPFに通して復調すると、入力信号がそのまま再生されるのではなく、直流バイアス電圧が重畳した形で再生されます。また、再生信号の振幅も、もともとの入力信号とは異なります。
入力信号を再生するために使うべき信号は、OUT信号より、むしろそれを1ビットD/A変換回路(レベルシフト回路)を通して得られたv3(t)です。v3(t)は、OUT信号と同じタイミングで変化する2値信号ですが、−VMまたはVMの電圧を出力します。このOUT信号を、通過帯域の利得が1のLPFに通すと、入力信号vin(t)が、オフセット電圧なしで、振幅も正確に再生されます。
減算回路によりvin(t)からv3(t)を引いて得られるv1(t)はA/D変換出力の入力信号の近似誤差、つまり量子化ノイズを表しています。(以後、量子化ノイズを単にノイズと呼びます)
注:A/D変換出力の入力信号の近似誤差は、普通はA/D変換信号v3(t)から入力信号vin(t)を引いて求めるので、そういう意味で厳密にいえば、−v1(t)がノイズ波形になります。以下、ノイズのスペクトルの話をしますが、スペクトルの強度の観点からは、−v1(t)をノイズと呼ぼうと、v1(t)をノイズと呼ぼうと同じ議論になります。
ノイズ波形v1(t)を見ると、スパイク状の鋭い波形になっており、高い周波数の成分が多くあることが分かります。
一方で、入力信号をコンパレータで2値化し、A/D変換した場合は、ノイズが広い周波数に分布する事が知られています。
図9の1ビットA/D変換器のノイズ(v1(t))のスペクトルと、コンパレータによりA/D変換した場合のノイズのスペクトルを比較したのが図26です。
図26の青い曲線は図9のΔΣ型1ビットA/D変換器のノイズのスペクトルを示したグラフです。また図26の赤い水平線は、コンパレータで入力信号を2値化しする事により単純にA/D変換した場合のノイズのスペクトルを示したグラフです。
青い線では、低周波数領域でノイズが少なくなっており、高周波領域でノイズ成分が多くなっています。
それに対して、赤い線では、低い周波数から高い周波数まで、一定の強度でノイズが存在しています。(ホワイトノイズ)
青い線でも、赤い線でも、全周波数に渡って積算したノイズの量は、ほとんど同じです。これは、NビットA/D変換器のS/N比の理論的な上限が、6.02N+1.76[dB]で与えられるため(EDN JapanのA-D性能の理論と現実という記事を参照)、1ビットのA/D変換器の場合は、N=1として、S/N比の上限が7.78[dB]と決まってしまうからです。すなわち、フルスケールの信号に対し、−7.78[dB]以上のノイズが原理的に発生します。
信号電力とノイズ電力の比は、回路構成によらず、A/D変換のビット数でほぼ決まるのですが、ノイズのスペクトルは、回路構成により変わります。
先ほど述べた様に、ΔΣ型のA/D変換器は、ノイズが高周波領域に偏って分布します。(図26の青線を参照) そのため図26のグラフを見ると、コンパレータによる単純なA/D変換をした場合(赤線)の低周波数領域のノイズのかなりの部分(赤い斜線部)が、ΔΣ型のA/D変換器を使うと高周波数領域(青い斜線部)に移動する様に見えます。
この様に、ΔΣ型のA/D変換器を使う事により、低周波領域のノイズを低減し、その分を高周波数領域に移動させる(様に見える)処理の事をノイズシェーピングといいます。
参考:シェーピング(shaping)は、成形という意味です。
ここでは図9に示すΔΣ型A/D変換器でノイズシェーピングが起こる仕組みを、定性的に説明します。
前項で述べたように、減算回路の出力電圧v1(t)はノイズ波形(の正負を反転させた波形)を表しています。このv1(t)が積分回路によって、時間積分され、v2(t)が出力されます。
積分回路の利得は周波数に反比例するため、低周波数成分が強調され、高周波数成分が減衰します。この事は、積分回路が、利得の平坦部がない、一種のLPFとして機能する事を示しています。(図27参照)
参考:積分回路の利得が周波数に反比例する事は、sin2πftという、周波数がfの正弦波を、tで積分すれば分かります。sin2πftdt=−12πfcos2πftなので、積分結果の振幅は1fに比例します。つまり周波数fに反比例します。
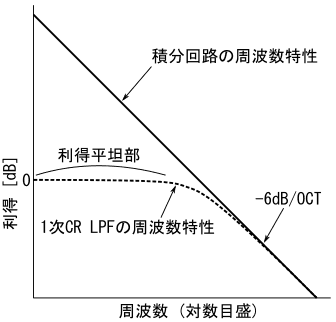
参考のため、ここでは積分回路以外に1次CR LPFの周波数特性も合わせて載せています。積分回路の利得は、周波数と反比例するため、両対数グラフ(縦軸の利得は線形目盛だが単位がdBなので実質は対数目盛)で見ると、−6[dB/OCT]の傾きを持った、右肩下がりの直線のグラフになります。この事は、積分回路が、利得平坦部のない一種の1次LPFだと解釈できる事を示しています。
ノイズv1(t)を積分回路に通して得られるv2(t)は、v1(t)よりも低周波数成分が強調され、高周波数成分が減衰しています。
このv2(t)をヒステリシスコンパレータで2値化し、減算回路に負帰還させるので、v2(t)のスペクトルが平坦化する様に、回路が動作します。
v2(t)は、ノイズv1(t)の高周波成分を減衰させたものですから、v2(t)のスペクトルが平坦ならば、v1(t)のスペクトルは、高周波数になるほど強くなります。これがノイズシェーピングが起こる原理です。
ノイズをLPFに通してから負帰還を掛けるのがノイズシェーピングの原理だとすれば、積分回路を1個使った1次のLPFを使う代わりに、積分回路を2個以上使う高次のLPFを使えば、LPFの利きが鋭くなるため、ΔΣ型A/D変換器のノイズを、さらに高周波領域に局在化できるはずです。
Bluefish WebpageというサイトのプログラムでΔΣ変調器というページでは、プログラムを組んでΔΣ型の1ビットA/D変換器が発生するノイズについてシミュレーションしています。
このページでは、1次の(積分回路を1個使った)ΔΣ型A/D変換器と2次の(積分回路を2個使った)ΔΣ型A/D変換器の特性をシミュレーションして、それらを比較していますが、適切に設計された2次のΔΣ型A/D変換器は、1次のΔΣ型A/D変換器よりも、ノイズシェーピングの効果が高いという結果が示されています。
また、2次のΔΣ型A/D変換器では、設計パラメータの設定が悪いと、負帰還制御がうまく収束せず、出力信号が、入力信号とは無関係に発振する事も示されています。
後で説明する様に、1ビットのΔΣ型A/D変換器の出力をデジタルLPFに通し、さらにダウンサンプリングする事で、等価的に多ビットのA/D変換器を構成する事がよくあります。この場合は、ノイズがより高周波数領域に集中するΔΣ型A/D変換器を用いると、それを使ってできた多ビットのA/D変換器の性能が向上します。
そのため、実用の際には、5次以上の高次のΔΣ型A/D変換器が使われる事が多いのですが、ΔΣ型A/D変換器の次数が高いほど設計時に決定しなければならないパラメータが多くなり、しかもそれらのパラメータの設定値が不適切だと、出力が発振します。
高次のΔΣ型A/D変換器の設計には、かなりの知識とノウハウが必要で、事前の特性のシミュレーションも綿密に行う必要があります。
図28に示す様に、1ビットのΔΣ型のA/D変換器を用い、十分高いサンプリング周波数fSでアナログ入力信号をA/D変換した結果を、ビット長拡張した後にデジタルLPFに通す回路を考えます。
図28にビット拡張器というのがありますが、これは、A/D変換器から受け取った信号を定数倍して、ビット数を増やす操作を行う装置です。通常は2倍、4倍、8倍、16倍、・・・と、2の自然数乗倍するのが普通です。それなら、受け取った数字の後ろに0をいくつか足す(2進数表記の場合)だけで済みます。(この記事では、2進数の数字は、暗めの緑色で表記します)
例えば、受け取った数が0(電圧はL)なら000、受け取った数が1(電圧はH)なら100という具合に、受け取った数の後ろに2個の0を足すと、1ビットΔΣ型A/D変換器の出力を1ビットから3ビットに拡張できます。この場合、拡張後のビット長Nは3になります。
ビット長を拡張するのは、この直後にデジタルLPFを通す際に、多ビットの信号を扱うからです。
デジタルLPFというのはデジタルフィルタの一種で、A/D変換され、数値化された信号に何らかの計算を行う事により、フィルタの効果を得る計算回路の事です。
図29は、デジタルLPFを通す前後のノイズの様子の変化を表した図です。
この様に、ノイズシェーピングにより高周波数領域に集中していたノイズが、デジタルLPFによりごっそりと落とされるので、信号のS/N比が向上します。
デジタルLPFによりS/N比が向上したので、1ビットA/D変換時のS/N比の上限(7.78[dB])を超えて、複数ビット相当のS/N比(2ビットなら13.80[dB]、3ビットなら19.82[dB]、…)が得られます。
参考までに6.02N+1.76[dB]で与えられる、Nビット信号の理論的なS/N比を、Nを1~16の範囲で変えて計算した結果を、表1に掲載しておきます。
| デジタル信号のビット数 N[ビット] |
理論的なS/N比 [dB] |
|---|---|
| 1 | 7.78 |
| 2 | 13.80 |
| 3 | 19.82 |
| 4 | 25.84 |
| 5 | 31.86 |
| 6 | 37.88 |
| 7 | 43.90 |
| 8 | 49.92 |
| 9 | 55.94 |
| 10 | 61.96 |
| 11 | 67.98 |
| 12 | 74.00 |
| 13 | 80.02 |
| 14 | 86.04 |
| 15 | 92.06 |
| 16 | 98.08 |
参考:最終的に14dB前後のS/N比が得られれば2ビット、20dB前後のS/N比が得られれば3ビットという具合に、表1を参考に、出力する信号のビット長を決める事になります。ただし、デジタルLPFの演算において、丸め誤差が信号品質に影響しない様に、途中の演算では、最終的な信号のビット長よりも長めにしておく必要があります。図28中のビット長拡張器において、信号を何ビットに拡張するかは、最終的な出力のビット長と、計算過程における丸め誤差を考慮して決めます。
この様に、1ビットのΔΣ型のA/D変換器を用い、十分に高いサンプリング周波数fSで信号をA/D変換し、デジタルLPFで高周波数のノイズを低減する事により、複数ビットのA/D変換が等価的に行えます。
上記の様に、ノイズシェーピングとデジタルLPFによりS/N比を上げるには、信号の周波数に対して、サンプリング周波数fSを十分に高くしなければなりません。
ノイズシェーピングとデジタルLPFによるS/N比の向上を狙わない場合は、サンプリング定理より、観測したい信号の周波数の上限をfmaxとすると、サンプリング周波数fSはfmaxの2倍の2fmaxに設定すれば十分です。
S/N比を向上させたい場合は、fSはさらにM倍(Mは2以上の整数に選ぶ場合が多い)のf=2Mfmaxに設定します。この時、「M倍オーバーサンプリングする」と表現します。
参考までに、オーバーサンプリングを行わない場合の信号とノイズの分布を図30に、2倍オーバーサンプリングする場合の信号とノイズの分布を図31に、3倍オーバーサンプリングする場合の信号とノイズの分布を図32に示します。
これらの図を比較すると、オーバーサンプリングの倍数が大きいほど、信号の上限周波数fmaxよりも高周波の領域に、ノイズが多く分布する事が分かります。
つまり、オーバーサンプリングの倍数が大きいほど、デジタルLPFでノイズを低減しやすくなり、S/N比が大きく向上できる事になります。
ノイズシェーピングとオーバーサンプリングをした1ビットのA/D変換結果を、デジタルLPFに通して、高周波数領域のノイズをカットすると、S/N比が向上し、複数ビットのA/D変換器が等価的に構成できる事を、前項で説明しました。
この項では、その複数ビットのA/D変換結果をダウンサンプリングする事によってサンプリング周波数を下げ、見かけ上の情報量を減らす事について説明します。
先ほど示した図31は、2倍のオーバーサンプリングにより、1ビットのΔΣ型A/D変換器で信号をA/D変換した結果を示しています。
図31のA/D変換した信号を、ビット長拡張した後に、図33の様な、観測したい信号が存在する上限の周波数fmax以上で急峻に減衰するデジタルLPFに通すと、図34の様に、信号は減衰せずに、fmax以上の周波数のノイズが減衰します。
この様にして、デジタルLPFで高周波数のノイズを低減する事で、S/N比が向上し、多ビットのA/D変換に等価的になる事は、前項でも説明しました。
しかし図34の信号とノイズの周波数分布をみていると、観測したい信号がfmaxまでの周波数にしか存在しないのに、サンプリング周波数fSが4fmaxもあるのは、無駄である事に気が付きます。サンプリング定理によると、サンプリング周波数は半分の2fmaxで十分なはずです。もし、サンプリング周波数を半分に落とせるなら、見かけ上の情報量が半分に減ります。
注:信号が完全に再生される様にサンプリング周波数が落とせるなら、見かけ上の情報量が減っても、実際の情報量は減りません。つまり、サンプリング周波数を落とす事により、冗長な情報を減らす事ができるのです。
どのようにすればサンプリング周波数を半分にできるかといえば、図35に示す様に、サンプルを1つ置きに捨てればいいのです。
図35の様に、サンプルを間引きしてサンプリング周波数を整数分の1にする事を、ダウンサンプリングまたはデシメーションといいます。
図35の場合は、サンプリング周波数を12にするダウンサンプリングでしたが、もしサンプリング周波数を13にしたいなら、図36の様に、1つのサンプルを残して、続く2つのサンプルを捨てて、続く1つのサンプルを残して、続く2つのサンプルを捨てて…という具合に、もともとの 23のサンプルを間引く事になります。
12にダウンサンプリングする場合、fS4以下の周波数成分は、変化することなく半分のサンプリング周波数の信号に変換されますが、fS4~fS2の範囲の周波数の信号は、周波数が変化してしまいます。
図37は、fS4~fS2の範囲の周波数の信号(黒線)を12にダウンサンプリングした様子を示しています。△は、元のサンプリング周波数のサンプルを示しています。〇は、△のサンプルを1つ置きに間引いて、半分のサンプリング周波数にしたものです。〇のサンプルのみを線でつなぐと、赤線の様に、元の信号(黒線)よりも低い周波数の信号が現れます。この様に、ダウンサンプリングで現れる、元の周波数よりも低い偽の信号を折り返し雑音とかエイリアスといいます。
図38は、信号と折り返し雑音の周波数関係を示した図です。
図38には、サンプリング周波数fSでサンプリングされた信号Aと信号Bが描かれています。(信号Aと信号Bが重畳した信号がサンプリングされたと考えても、信号Aをサンプリングしたデータと信号Bをサンプリングしたデータが別々にあると考えても構いません) 信号Aの周波数はfA、信号Bの周波数はfBとします。そして、fS4<fA<fS2およびfS4<fB<fS2が成立しているとします。
fS4<fAとfS4<fBが成立しているので、12のダウンサンプリングをして、サンプリング周波数がfS2になると、信号Aや信号Bはナイキスト周波数fS4を超えるため、折り返し雑音になります。
信号Aの折り返し雑音をエイリアスA、信号Bの折り返し雑音をエイリアスBとしすると、エイリアスAの周波数はfS2-fA、エイリアスBの周波数はfS2-fBとなります。この様子をグラフ上で見ると、周波数fS/4を対象軸に折り返したように見えるので、「折り返し雑音」という用語を使うのです。
ここで、図34の信号および雑音を12のダウンサンプリングするとどうなるかを考えてみます。
信号についてはfS4以下の周波数帯域にしか存在しないので、ダウンサンプリングしても、折り返し雑音が発生する心配はありません。
一方で、ノイズに関しては、fS4以上の周波数領域にも成分がありますので、この成分が、ダウンサンプリングにより折り返し雑音になります。この様子を表したのが図39です。
ノイズの内、fS4以上の周波数成分は、周波数fS4を対称軸に折り返して、赤い点線の様になります。fS4以下の周波数領域に元々あった赤い実線のノイズ以外に、赤い点線の折り返し雑音も加わりますので、ノイズの電圧密度は上昇し、紫色の実線がダウンサンプリング後のノイズの分布になります。
紫色の線を見ると、赤線よりはノイズの電圧密度が上昇する事になりますが、一方で、ダウンサンプリング後はfS/4以上の周波数領域のノイズがなくなります。トータルで考えると、ダウンサンプリングの前後でS/N比に変化はありません。
以上の様に、信号を2倍のオーバーサンプリングして、ΔΣA/D変換器で発生した高周波領域のノイズをデジタルLPFで低減し、さらに1/2のダウンサンプリングをする事で、1ビットのA/D変換器では得られない、高いS/N比を得られる事が分かりました。
この処理をする回路のブロック図は、図28のブロック図の後に12のダウンサンプリングをするブロックを追加して、図40の様になります。(図では2倍オーバーサンプリングではなく、もっと一般的にM倍オーバーサンプリングの処理回路について示しています)
この節では、話を複雑化させない様に、2倍オーバーサンプリングの場合について取り上げましたが、オーバーサンプリングの倍数が高いほど、S/N比向上の効果が大きいため、通常はもっと高い倍率でオーバーサンプリングします。例えばオーディオ信号をA/D変換する場合は、128倍などの高い倍数で、信号をオーバーサンプリングします。
