| 2020年02月06日 | 更新 |
ΔΣ変調をA/D変換に用いる場合について説明します。
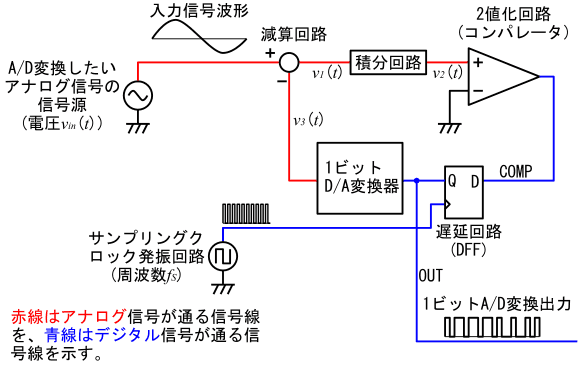
1ビットのA/D変換を行うΔΣ変調器としては、比較的単純な図9の回路を用いて、A/D変換の原理を説明します。
図9の回路は、前のページの図1に示したPDM変調回路と、回路構成が似ていますし、回路動作も似ています。
両者を比較すると、図1のPDM変調回路ではヒステリシスコンパレータを使っているのに対し、図9の1ビットA/D変換器では、ヒステリシスのないコンパレータを用いている所が違います。また、図9の回路では、遅延要素(DFF)を持っている点が特徴的です。
回路動作の点で図1の回路と図9の回路を比較すると、どちらの回路でも、出力のパルス波形は、パルスの密度で信号を表現しており(つまりPDM変調しており)、LFPに通すと、入力したアナログ信号が再生される点が共通しています。
注:厳密にいえば、図9の回路では、入力信号そのものではなく、入力信号に直流オフセット電圧が加わった信号が再生されます。
ただし、図1の回路では、出力信号の電圧は2値化されている(LまたはHの信号しか取らない)ものの、時間軸方向には離散化(標本化)されていません。つまり、図1の回路は広義のアナログ回路です。
一方で、図9の回路では、出力信号の電圧が2値化されているのに加えて、時間軸方向にも離散化されており、サンプリングクロック信号に同期して出力電圧が変化します。つまり、図9の回路の出力信号は、ディジタル信号です。図9の回路が1ビットのA/D変換回路と呼ばれるのは、この事によります。
出力信号が時間軸方向に離散化されている図9の回路と、自由なタイミングで出力電圧が変化できる図1の回路とを、出力信号の発振周波数が同程度という条件で比較すると、図1の回路の方が多くの情報を含んだ(ノイズの少ない)出力信号が出てきます。
図9の回路でノイズの少ない高品位な出力信号を得ようとすると、後述する様に、オーバーサンプリングの倍数を増やし、十分に高いサンプリング周波数(サンプリングクロック信号の周波数)で回路を動作させる必要があります。(こうすると、必然的に出力信号の発振周波数が上がります)
図1の回路と図9の回路では、減算回路と積分回路は、同様の動作をします。
コンパレータに関しては、図9の回路では、ヒステリシスのない、単純な特性のコンパレータを用います。入力電圧が正の値ならば、出力電圧はVH(論理回路でHを表す電圧)となり、入力電圧が負の値なら、出力電圧はVL(論理回路でLを表す電圧で、普通は0[V]に設定される)になります。(図10参照)
図1の回路にはなく、図9の回路にある要素としては、Dフリップフロップ(DFF)を用いた遅延回路があります。DFFは、サンプリングクロック信号の立ち上がり(LからHの電圧変化)のタイミングで、D端子の電圧を取り込み、Q端子に出力します。次のクロック信号の立ち上がりまではQ端子の電圧は変化しません。(図11参照) DFFのこの働きにより、D信号とQ信号の間で、最大1クロック分の遅延が発生します。
参考:Dフリップフロップについてもう少し詳しく知りたい場合は、この用語集のDフリップフロップの項目をご覧ください。
図9の1ビットD/A変換器は、「D/A変換器」という大げさな名前が付いていますが、実態はただのレベル変換器です。1ビットD/A変換器は、入力電圧がVLの場合は出力電圧が−VMになり、入力電圧がVHの場合は出力電圧がVMになります。(図12参照)
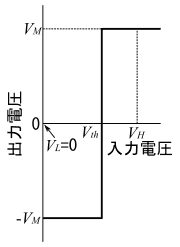
閾値電圧Vthを、VLとVHの中間の電圧に設定し、入力電圧がVthより高ければVMを出力し、入力電圧がVthより低ければ−VMを出力します。
VMの値は、全ての時間で(任意のtの値で)入力信号vin(t)が式(10)を満たす様な、大きな値に設定する必要があります。
図13に示す様に、入力電圧が直流電圧VSの場合の回路の動作について説明します。
まず、減算回路の動作について考えます。+側端子の電圧はVS、−側端子の電圧はv3(t)ですから、減算回路の出力電圧v2(t)は、式(11)で与えられます。
積分回路は入力電圧を時間積分し、その積分結果に正の係数Kを掛けた電圧を出力します。よって、積分回路の出力電圧v2(t)は、式(12)で与えられます。
DFFの出力信号であるOUT信号は、LまたはHのいずれかになりますが、ここでOUT信号がLの場合とHの場合に分けて、順に説明します。
まずOUT信号がLの場合について考えます。
この時、1ビットD/A変換器の出力電圧v3(t)は−VMになります。すなわち、式(13)が成立します。
これを式(12)に代入すると、式(14)が得られます。
参考:この式は、式(5)と同じ式です。
式(10)より、VSの値が正であれ、負であれ、VM+VS>0となりますから、v2(t)は正の定数となります。よって、v2(t)は傾きK(VM+VS)の、右肩上がりの一次関数になります。
今度はOUT信号がHの場合につて考えます。
この時、1ビットD/A変換器の出力電圧v3(t)はVMになります。すなわち、式(15)が成立します。
これを式(12)に代入すると、式(16)が得られます。
式(10)より、VSの値が正であれ、負であれ、VM−VS>0となりますから、v2(t)は負の定数となります。よって、v2(t)は傾き−K(VM−VS)の、右肩下がりの一次関数になります。
v2(t)>0になればDFFによって生じる遅延時間の後にOUT信号がHになり、また逆にv2(t)<0になればDFFによって生じる遅延時間の後にOUT信号がLになります。この事と、式(14)および式(16)とを考え合わせると、図13の回路の各所の動作波形は図14の様になります。
図13の回路は、減算回路にv3(t)とVSが入力されている事から分かる様に、v3(t)の時間平均値がVSと一致する様に、負帰還が掛かっています。つまり、OUT信号のパルス密度で、入力電圧VSを表現します。(PDM変調)
OUT信号のデューティ比をDとすると、v3(t)の時間平均値がVSと一致する条件より、式(17)が得られます。
VSの変化に対してDがどう変化するのかを表したグラフが図15です。このグラフに示す様に、VS=−VMの時にD=0、VS=0の時にD=0.5、VS=VMの時にD=1になるような、一次関数のグラフになります。
OUT信号がHの時の出力電圧をVHとし、OUT信号がLの時の出力電圧VLが0に設定されているものとして、OUT信号を、通過帯域の利得が1のLPFに通して復調すると、DVHという電圧が得られます。この事から、図9(あるいは図13)の回路の出力をLPFに通して信号を復調すると、元の信号に直流バイアス電圧0.5VHが重畳された信号が得られる事が分かります。
VSの値を色々変えながら、入力信号、CLK信号およびOUT信号の波形を描いた例を図16~図20に示します。
VSが大きな値の時ほど、出力信号(OUT信号)のデューティ比が大きくなっている様子が分かります。
また、VSが正の値の場合はパルス間隔(Lになっている時間)が1クロックで、VSが0の場合は、LとHが1クロックごとに交互に現れ、VSが負の値の場合はパルス幅(Hになっている時間)が1クロックである事も分かります。
VS≧0の場合とVS<0の場合に分けて、OUT信号の発振周期Tおよび発振周波数fを求めます。
VS≧0の場合は、OUT信号の1周期の内、Lになっている時間が1クロックです。つまり、OUT信号の発振周期Tは、式(18)の様に求まります。
ここで、fSはサンプリング周波数(サンプリングクロックの周波数)です。つまり1fSが1クロックの時間(サンプリング間隔)になります。
注:式(18)からOUT信号の周期Tを求めると、一般にクロック周期(1fS)の実数倍の長さになります。Tがクロック周期の整数倍の長さになるには、特別な条件が必要です。例えばVS=0の場合はTは2クロック(図21参照)、VS=VM3の場合はTは3クロック(図22参照)となり、整数のクロック数になりますが、VS=1VMの場合はTは2.5クロックと、非整数のクロック数になります。OUT信号はサンプリングクロック(CLK信号)と同期して出力されますから、周期が非整数のクロック数になるのは、一見しておかしい様に見えます。しかしTが2.5クロックの場合は、実際には2クロック周期(ここでの周期はある波形の立ち上がりから次の波形の立ち上がりまでの時間を指します)のパルスと、3クロック周期のパルスが交互に発生します。(図23参照) この様に、式(18)で求まる周期は、平均的な周期を指します。
Tの逆数がOUT信号の発振周波数fになりますから、fは式(19)の様に求まります。
VS<0の場合は、OUT信号の1周期の内、Hになっている時間が1クロックです。つまり、OUT信号の発振周期Tは、式(20)の様に求まります。
Tの逆数を取って、OUT信号の発振周波数fを求めると、式(21)の様になります。
式(19)と式(21)から、入力電圧VSを−VM~VMの範囲で変化させた場合に、OUT信号の発振周波数fがどのように変化するかをグラフ化したのが、図24です。
VS=−VMの時とVS=VMの時にfが最低値0を取り、VS=0の時にfが最大になるという点では、図24は図7と同じです。しかし、図7のグラフが上に凸の放物線なのに対し、図24のグラフは、VS=0で折れ曲がった直線のグラフになっています。
また、図7のグラフの最大値はK4VTと積分回路の定数Kの影響を受けますが、図24のグラフの最大値はFS2と、Kには無関係に決まります。これは、図1(または図5)の回路では、積分回路の出力電圧を−VTまたはVTという0以外の定数と比較しているのに対し、図9(または図13)の回路では、積分回路の出力電圧を0と比較しているからです。0と比較するのなら、積分回路の出力電圧が定数倍になっても、回路の動作は変わりません。
次のページでは、ノイズシェーピングとオーバーサンプリングによる多ビットのA/D変換器の構成方法について説明します。
