| 2018年07月12日 | 公開。 |
| 2018年08月31日 | LTspiceがLTSpiceと表記されていたのを改めた。 |
opampの出力インピーダンスについて確認してみましょう。
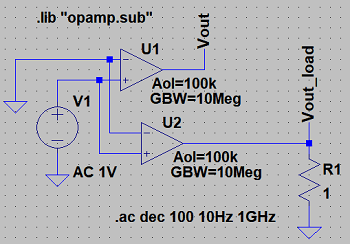
opampの利得とGB積をデフォルトの100dBと10MHzに戻して、図31の回路を入力します。
この回路には、2つのopamp(U1とU2)があります。これらの特性は同一なのですが、U1の方には出力に負荷が付いておらず、U2の方には出力に1Ωの負荷が付いています。
U1とU2の周波数特性は図32の様になります。
緑の曲線は無負荷のU1の周波数特性を、青の曲線は1Ω負荷のU2の周波数特性を表わしています。低い周波数領域での利得がU1では100dBになっていますが、U2では6dBダウンして94dBになっています。
実は、opampの低周波領域の出力インピーダンスは1Ωに設定されています。そのため、低周波領域では、図33に示す分圧回路が形成され、出力が半分(利得が6dBダウン)になるのです。
高い周波数まで考えると、デフォルト設定のopampの出力インピーダンスは1Ω//1592μFとなっています。(理由は後述)
注:ただし利得がデフォルトの100dBでGB積がデフォルトの10MHzの場合です。利得やGB積の設定が変わると、コンデンサの容量が変わります。
周波数が上がると1592μFのコンデンサのインピーダンスが周波数に反比例して低くなるため、負荷の影響を受けにくくなります。図32のグラフでも、周波数が高くなると、U1とU2の利得がほぼ一緒になっているのが確認できます。
残念ながら、opampでは出力インピーダンスを変更する事はできません。直流での出力インピーダンスは必ず1Ωです。1Ωというのはオペアンプの出力インピーダンスとしては低い値ではありますが、0ではありません。
この1Ωの出力インピーダンスにより、大電流を扱う回路では電圧降下が無視できなくなり、理想オペアンプと異なるシミュレーション結果が出そうな気がしますが、実は、意外とその影響は小さいのです。
オペアンプは通常、負帰還を掛けた形で使われます。負帰還がかかると、その帰還量に応じて、見かけ上のオペアンプの出力インピーダンスが下がるので、1Ωの出力インピーダンスがあるオペアンプを使っても、実際にははるかに小さいインピーダンス分の電圧降下しか発生しません。
本題から離れますので、ここでこの話を定量的に議論するのは避けますが、定性的には次の様な事が生じます。
図34の様な、オペアンプを用いたボルテージフォロワ回路があるとします。このオペアンプは、出力インピーダンスが1Ωであること以外は、理想オペアンプと同じ特性を持っていると仮定します。(利得とGB積を極端に上げたopampをイメージしてください)
オペアンプの非反転入力端子に1Vの直流電圧が入力されていますが、ボルテージフォロワ回路なので、出力電圧Voutも1Vです。
次に、このボルテージフォロワ回路の出力に、図35の様に1Ωの負荷抵抗を付けたとします。
(1)負荷抵抗を付けた瞬間は、(2)オペアンプの出力抵抗Roと負荷抵抗RLが構成する分圧回路により、出力電圧が半分の0.5Vに下がろうとします。
そうすると、(3)反転入力端子の電圧が下がるのをオペアンプが検知し、出力電圧を上げます。オペアンプは、反転入力端子の電圧が非反転入力端子の電圧(1V)よりも低い間は、出力電圧を上げようとしますので、その結果、(4)出力電圧がちょうど1Vになったところで、反転入力端子と非反転入力端子の電圧が同じになり、出力電圧が安定します。
GB積が無限大の理想的なオペアンプでは、(1)~(4)のプロセスにかかる時間が0なので、負荷をつないでも電圧は全く変化しません。
注:GB積が有限の現実のオペアンプでは、(1)~(4)のプロセスにかかる時間が有限なので、負荷をつなぐと、一瞬出力電圧が低下します。
また、利得が無限大の理想的なオペアンプでは、反転入力端子の電圧が1Vよりも少しでも低ければ出力電圧を上げようとしますので、負荷をつないでからの出力電圧が安定した後の出力電圧は完全に1Vになります。
注:利得が有限の現実のオペアンプの場合には、非反転入力端子の電圧(1V)と反転入力端子の電圧(=出力電圧)を利得倍した物が、内部抵抗で電圧降下が起こる前のオペアンプの出力電圧(図35のオペアンプの出力抵抗Roの左側の電圧)となった時点でつり合ってしまいます。その結果、出力電圧が1Vよりもわずかに下がってしまいます。
話をまとめると、オペアンプに内部抵抗(や内部インピーダンス)があっても、利得と帯域(GB積)が十分であれば、出力抵抗の影響は、負帰還によりキャンセルされます。よって、負帰還を掛ける使い方であれば、十分大きな利得とGB積に設定したopampの出力インピーダンスについては考える必要がないのです。
話が長くなりましたので、理想オペアンプを使った回路のシミュレーションを、opampを使って行う場合の要点を、まとめます。
"opamp.sub"の内容を読むと分かるのですが、デフォルト状態の"opamp"の中身は、実は図36の様な回路になっています。
"NON-INVERTED INPUT"と書いてあるのが非反転入力端子、"INVERTED INPUT"と書いてあるのが反転入力端子、"OUTPUT"と書いてあるのが出力端子です。
図36の中央に"G1"という丸い部品がありますが、これは電圧制御線形電流源(あるいは単に電圧制御電流源)と呼ばれるものです。
図37に、電圧制御電流源の記号の説明図を示します。
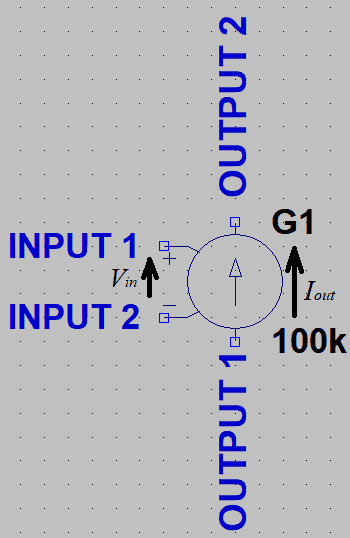
"INPUT 1"と書いてある端子と"INPUT 2"と書いてある端子が入力端子です。また"OUTPUT 1"と書いてある端子と"OUTPUT 2"と書いてある端子が出力端子です。
電圧制御電流源は、入力電圧に比例した電圧に比例した電流を出力する電流源です。"INPUT 2"の端子を基準にした"INPUT 1"の端子の電圧(Vin)を定数倍した電流(Iout)を、"OUTPUT 1"の端子から"OUTPUT2"の端子の方向に流します。
出力電流Ioutを入力電圧Vinで割った値を相互コンダクタンスといい、単位はS(ジーメンス)です。相互コンダクタンスはしばしばgmという文字で表わされますが、ここでも相互コンダクタンスをgmと表記する事にします。
電圧制御電流源の特性を表わす値はgmのみです。図37の電圧制御電流源の場合は、gm=105(100k)となっています。
電圧制御電流源の入力インピーダンスは無限大で、入力端子(INPUT 1とINPUT 2)に電圧をいくら印加しても、電流は流れません。
電圧制御電流源の出力インピーダンスも無限大で、出力端子間(OUTPUT 2とOUTPUT1の間)の電圧にかかわりなく、流れる電流は一定(gmVin)です。
ここで、図36のデフォルト状態の"opamp"の中身に話が戻ります。
G1のgmが105なので、非反転入力端子と反転入力端子の間に電圧がかかると、その倍105の大電流が"G1"の出力端子から流れ出します。その電流は、"R1"の1Ωの抵抗と"C1"の1592μFのコンデンサの並列回路に流れ込みます。
今、直流の場合を考えると、コンデンサはオープンしているものとして無視していいですから、"G1"から流れ出た電流は"R1"を流れ、そこで電圧が発生します。"R1"は1Ωですから、"R1"に流れた電流が、そのまま"R1"で発生する電圧になります。
結局、直流においては、非反転入力端子の電圧と反転入力端子の電圧の差を、105倍して出力端子に出力する事になります。よって、105倍の大きな増幅率を持つ差動増幅器、すなわちオペアンプとして動作します。
交流の場合を考えると、出力電圧は"R1"と"C1"の並列回路のインピーダンスに、電流gmVinを掛けて得られる電圧が発生します。
"R1"の抵抗値をR1(=1Ω)、"C1"の容量をC1(=1592μF)とすると、それらの並列インピーダンスZは、次の式で与えられます。
ここでjは虚数単位(-1)、πは円周率、fは周波数を表わします。
1≫2πfC1R1が成立する低い周波数では、次の近似式が成立します。
よって、この周波数領域ではC1の影響は無視でき、インピーダンスはR1でほぼ一定となります。
逆に1≪2πfC1R1が成立する高い周波数では、次の近似式が成立します。
よって、この周波数領域ではR1の影響が無視でき、インピーダンスはC1のインピーダンスでほぼ近似できます。C1のインピーダンスは周波数に反比例して減少していきます。
式(2)が成立する領域と式(3)が成立する領域の境目では1=2πfC1R1が成立します。その時の周波数をカットオフ周波数と呼び、f0で表わす事にします。
f0は、次の式で与えられます。
カットオフ周波数においては、式(1)のfに式(4)のf0を代入する事により、インピーダンスZは次の様に求まります。
周波数fとインピーダンスZの大きさの関係をグラフにすると図38の様になります。
"opamp"の出力電圧をVoutとすると、Voutは次の式の様に求まります。
出力電圧Voutを入力電圧Vinで割った値Aの事をオープンループ電圧利得(あるいは単にオープンループゲイン)と呼びます。
式(5)より、Aは次の式で求まります。
f≪f0が成立する低い周波数では、近似的に次の式が成立します。
"opamp"では必ずR1=1[Ω]ですから、直流(あるいは十分低い周波数)のオープンループ電圧利得は、前述のとおり電圧制御電流源のgmそのものとなります。
一方で、f≫f0が成立する高い周波数では、近似的に次の式が成立します。
Aの大きさはfと反比例しますから、それらの積は、この周波数領域では一定になります。これがGB積です。
GB積をPGBと表わす事にすると、式(9)より、PGBは次の式で与えられます。
opampのデフォルト値では直流のオープンループ電圧利得"Aol"(gm)は105、"GBW"(PGB)は10MHzです。gm=105とC1=1592×10-6[F]とR1=1[Ω]を式(10)に代入すると、PGB=10×106[Hz]と求まるのが分かるでしょう。
逆に、"Aol"と"GBW"のパラメータをLTspice上で変更すると、gmは"Aol"の値に、C1は"Aol"を"GBW"で割りさらにと2πで割った値に変更され、式(10)が満たされる様に設定されます。
カットオフ周波数(f=f0)では、式(7)のfに式(4)のf0を代入する事により、Aは次の様に求まります。
オープンループ電圧利得Aの大きさと周波数fの関係をグラフにすると、図39の様になります。
図39により、図36の様な回路が、前のページの図22の様な周波数特性を持つ理由を説明できました。
ここまでの説明で、"C1"のコンデンサは、"opamp"の帯域制限のために設けられている事がお分かりでしょう。"C1"がなければ"opamp"のGB積は無限大になります。この話は、次の章の話と密接に関連があります。
次のページでは、電圧制御電圧源を使って理想オペアンプをシミュレーションする方法について説明します。
