↑ 画像をクリックすると拡大
図12、必ずLが入力されるNOT回路
| 2019年11月27日 | 更新 |
論理回路を論理圧縮する場合に利用できる、NOT回路の性質をいくつか説明します。
注:論理圧縮とは、元の回路と等価な論理回路を、なるべく少ない基本論理ゲートを用いて求める事を指します。
図12に示す様に、必ずLが入力されるNOT回路の出力は、必ずHになります。
図13に示す様に、必ずHが入力されるNOT回路の出力は、必ずLになります。
図14に示す様に、2つのNOT回路を縦続に接続した場合に、A点、B点、C点の電圧の関係を真理値表にすると表10の様になります。
| 入力電圧 | 中間電圧 | 出力電圧 |
|---|---|---|
| A | B | C |
| L | H | L |
| H | L | H |
表10より、入力電圧Aと出力電圧Cは、同じ電圧になる事が分かります。
この事は、図14に示した2つのNOT回路を縦続接続した回路が、図15に示すバッファ回路と等価である事を示しています。
ここでバッファ回路は、表11の真理値表に示す様に、入力電圧と同じ電圧を出力する回路の事です。
| 入力電圧 | 出力電圧 |
|---|---|
| A | C |
| L | L |
| H | H |
バッファ回路は、場合によってはA点とC点を結ぶ、ただの配線(図16参照)だと説明される事がありますが、バッファ回路とただの配線とは少し違います。
図15のバッファ回路の場合、A点は必ず入力端子で、C点は必ず出力端子です。よって、図17の様に、C点にNOT回路(U3)の出力を接続したり、A点にNOT回路(U1)の入力端子を接続したりする事ができません。
一方で、ただの配線なら、図18の様にC点にNOT回路(U2)の出力を接続し、A点にNOT回路(U1)の入力端子を接続し、C点からA点に信号を伝えられます。
他にも、バッファ回路には、ただの配線にはない、電流増幅作用や波形整形作用があります。
次に、図19の上側の回路の様に、NOT回路を偶数個縦続接続した場合を考えます。
NOT回路を2つ縦続接続した場合と同様の考察により、この回路が、図19の下側に示した様に、1つのバッファ回路と等価になる事が分かります。
図20の様に、3つのNOT回路を縦続に接続した場合を考えます。
A点～D点の電圧の関係を真理値表にすると、表12の様になります。
| 入力電圧 | 中間電圧 | 出力電圧 | |
|---|---|---|---|
| A | B | C | D |
| L | H | L | H |
| H | L | H | L |
この真理値表から分かる様に、入力電圧AがLの時は出力電圧DがHになり、入力電圧AがHの時は出力電圧DがLになります。
この事は、NOT回路を3つ縦続に接続した回路は、図21の様な、1つのNOT回路と等価である事を示しています。
次に、図22の上側の回路の様に、NOT回路を奇数個縦続接続した場合を考えます。
NOT回路を3つ縦続接続した場合と同様の考察により、この回路が図22の下側に示した様に、1つのNOT回路と等価になる事が分かります。
それでは、前章で説明したNOT回路の性質を利用して、論理圧縮をしてみましょう。2つの例題の回路をあげ、実際に論理圧縮してみます。
NOT回路の性質を利用しただけでは、複雑な回路を論理圧縮できませんから、次に示す、OR回路の性質も利用する事にします。
図23の様に、一方の入力にHが入力されたOR回路は、必ずHを出力します。
OR回路の一方の入力がHだと、もう一方の入力Aの値にかかわらず、出力Bの電圧はHになります。
また、図24の左側の回路の様に、一方の入力にLが入力されたOR回路の出力には、もう一方の入力のAがそのまま出力されます。つまりこの回路は、図24の右側の回路の様に、バッファ回路と等価になります。
OR回路の一方の入力にLが入力されていると、出力BにはAの電圧が出力されます。つまり、このOR回路は、Aを入力してBを出力するバッファ回路と等価です。
参考:OR回路の持つ図23や図24の性質は、OR回路の真理値表から簡単に証明できます。是非自分でこれらの性質を証明してみましょう。
それでは、例題1として、図25の回路を論理圧縮してみましょう。
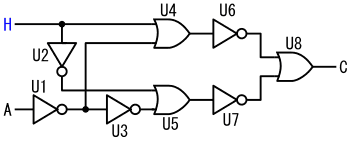
この回路にはNOT回路が5個、OR回路が3個ありますが、これら8個の基本ゲートに、U1～U8の部品番号を付けてあります。
この回路の入力は2つありますが、一方の電圧はHに固定されています。もう一方の入力にはAという信号名を付けています。
この回路の出力は1個で、Cという信号名を付けています。
今U2に注目すると、入力電圧が必ずHですから、図13に示したNOT回路の性質により、出力電圧はLになるはずです。この事により、U2を回路図より省く事ができます。実際にU2を省いた回路図を図26に示します。
ここでU4に注目すると、OR回路の一方の入力にHが入力されていますから、図23に示したOR回路の性質により、U4の出力は必ずHになります。
またU5に注目すると、OR回路の一方の入力にLが入力されていますから、図24に示したOR回路の性質により、U5は、U3の出力とU7の入力をつなぐ配線に置き換えられます。
注:図26の回路では、信号がU3の出力端子からU7の入力端子に向けて伝わるので、U3の出力信号を入力したバッファ回路の出力をU7の入力端子に接続する事は、U3の出力端子とU7の入力端子を配線でつなぐ事と同じである事に注意してください。
これらの理由により、図26の回路からU4とU5を省くと図27の様な回路になります。
ここでU6に注目すると、入力電圧が必ずHなので、図13に示したNOT回路の性質により、U6の出力電圧は必ずLになります。
またU1、U3、U7の3つのNOT回路について注目すると、3つのNOT回路が縦続に接続されているため、図22に示したNOT回路の性質により、これら3つのNOT回路は1つのNOT回路に置き換えられます。今、U1とU3を省いてU7を残す事にします。
これらの理由により、図27の回路からU1、U3、U6の3つのNOT回路を省くと、図28の回路になります。
ここでU8に注目すると、図24に示したOR回路の性質により、U8は、U7の出力とCを結ぶ配線に置き換えられる事が分かります。
図28の回路からU8を省くと、最終的に図29の様に、NOT回路が一つだけの回路が得られます。
この回路は、図28の回路からU8を省く事により得られます。
例題2として、図30の様な回路を論理圧縮してみます。この回路は、例題1で論理圧縮した図25の回路で、Hを入力していた左上の端子に、今度は逆にLを入力した回路となっています。
今U2に注目すると、図12に示したNOT回路の性質により、U2の出力電圧が必ずHになる事が分かります。
この理由により、図30の回路からU2を省くと、図31の回路になります。
ここでU4に注目すると、図24に示したOR回路の性質により、U4を取り除いて、U1の出力を直接U6に入力しても、動作が変わらない事が分かります。
またU5に注目すると、図23に示したOR回路の性質により、U5の出力電圧が必ずHになる事が分かります。この事により、U5が回路から省けます。さらに、U3の出力電圧はU5の出力電圧に影響しないため、U3も回路から省けます。
これらの理由により、U3、U4、U5の3つを図31の回路図から省くと、図32の回路になります。
ここでU1とU6に注目すると、図19に示したNOT回路の性質により、これら2つのNOT回路を回路から省き、AをU8の上側の入力端子に直接入力しても、回路の動作が変わらない事が分かります。
またU7に注目すると、図13に示したNOT回路の性質により、U7の出力電圧が必ずLになる事が分かります。
これらの理由により、図32の回路からU1、U6、U7の3つを省くと、図33の回路になります。
ここでU8に注目すると、図24に示したOR回路の性質により、U8は、Aを入力とし、Cを出力とするバッファ回路に置き換えられる事が分かります。
この置き換え操作により、最終的に図34の様な回路が得られます。
この回路は、図33の回路のU8を、バッファ回路に置き換えると得られます
図25(あるいは図30)の回路の左上の入力端子の電圧を、H(図25の場合)やL(図30の場合)に固定せずに、Bという信号名の信号にした、図35の様な回路について考えてみます。
例題1により、Bの電圧がHの場合には、出力CはAになる事が分かっています。
また例題2により、Bの電圧がLの場合には、出力CはAになる事が分かっています。
これらの事から、図35の回路の真理値表を作成すると、次の様になります。
| 入力信号 | 出力信号 |
備考
|
|
|---|---|---|---|
|
A
|
B
|
C
|
|
| L | L | L | C=A |
| L | H | H | C=A |
| H | L | H | C=A |
| H | H | L | C=A |
この真理値表を見ると、図35の回路は、図36に示すXOR回路と等価である事が分かります。
次のページでは、バイポーラトランジスタを用いたNOT回路の構成法と、NOT回路を使った記憶素子について説明します。
