| 2019年11月27日 | 更新 |
NOT回路は1入力1出力の2値論理回路の一種で、0を入力すると1を出力し、1を入力すると0を出力します。NOT回路はNOTゲート、論理反転回路、論理否定回路、あるいはインバータとも呼ばれます。また、NOT回路は、基本論理ゲートの一種です。
NOT回路の行う論理演算は、NOT演算、論理否定、あるいは論理反転と呼ばれます。
後述する様に、NOT回路は、入力信号から論理反転した信号を生成したり、正論理の信号と負論理の信号の変換に使われます。
NOT回路の回路記号を図1に、真理値表を表1に示します。
| 入力信号の真理値 | 出力信号の真理値 |
|---|---|
| X | Y |
| 0 | 1 |
| 1 | 0 |
この様に、入力電圧と反対の真理値を出力する事から、「反対の」という意味を込めて、NOT回路という名称が用いられています。
NOT回路の入出力の電圧(LまたはH)の関係を真理値表で表すと、正論理の回路の場合も、負論理の回路の場合も、表2の様になります。
| 入力電圧 | 出力電圧 |
|---|---|
| X | Y |
| L | H |
| H | L |
論理回路を数式表記したのを論理式といいます。信号XをNOT回路に通した信号を、論理式で表すと、Xとなります。
図1の回路は、論理式で表すと、式(1)になります。
参考1:NOT回路に通した信号全体に上線を付けます。例えばA+B(AとBの論理和)をNOT回路に通した場合、A+Bと表記します。
参考2:負論理の信号の名称に上線を付ける習慣は、NOT回路に通した信号の名前に上線を付けて表記する事に由来しています。
NOT回路を含む論理回路の働きを、集合論で使うベン図を使って表す事があります。この場合、集合としては、入力信号が取り得る真理値(複数入力の論理回路の場合は入力信号が取り得る真理値の組み合わせ)の集合を考えます。
集合と言っても論理回路ですから、入力信号が取り得る真理値全ての集合を考えても、要素は多くありません。特にNOT回路の場合は、入力信号がXの1つしかありませんから、全体集合Uは、Xの取り得る真理値の{0,1}となり、たった2つの要素の集合になります。
図2のベン図は、Uと書いた四角の領域が、全体集合(入力信号Xが取り得る真理値の集合){0,1}を表しています。またXと書いた円内部の領域は、X=1が成立する場合にXが取り得る真理値の集合{1}を表しています。Xの円の外側には、その円の集合の補集合である{0}があります。
このベン図において、X=1(この場合のXの上線は補集合ではなくNOT回路の出力を表す)になる場合に、Xが取り得る真理値の集合に色を塗る事を考えます。X=1になる時というのは、X=0になる時の事ですから、図3に示す様に、ベン図中のXと書いた円の外側の領域の、{0}の部分に色を塗るのが正解です。この図3が、NOT回路の働きを表すベン図になります。
図3を見て分かる様に、NOT演算は、ベン図上では補集合を求める操作に相当します。
NOT回路の持つ論理反転(あるいは論理否定)という基本的な性質を、正論理の回路の場合と負論理の回路の場合について、順に説明します。
図4の様に、プッシュスイッチのボタンが押されている(プッシュスイッチがONになった)事を表すPRESSEDという正論理の信号をNOT回路に入力して、プッシュスイッチのボタンが押されていない(プッシュスイッチがOFFになった)事を表すRELEASEDという正論理の信号を生成する回路について考えます。
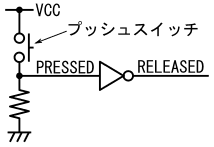
プッシュスイッチは押しボタンスイッチとも呼ばれます。スイッチに押しボタンが付いており、ボタンを指で押すかどうかで、ONとOFFを切り替えます。図2に使われているプッシュスイッチの場合、ボタンを指で押すとスイッチがONになり、ボタンから指を離すとスイッチがOFFになります。
図中のVCCは電源電圧を表しています。これ以降の図においても、VCCは電源電圧を表すものとします。
参考:"pressed"という英単語は「押された」という意味の形容詞です。また"released"という英単語は「離された」という意味の形容詞です。
PRESSED信号は、プッシュスイッチのボタンが押されていない時に偽(0)になり、ボタンが押されている時に真(1)になります。
PRESSED信号は正論理の信号ですから、プッシュスイッチのボタンが押されていない時に電圧がLになり、ボタンが押されている時に電圧がHになります。
これらの事をまとめると、表3の様になります。
| スイッチの状態 | 真理値 | 電圧 |
|---|---|---|
| ボタンが押されていない(スイッチOFF) | 0(偽) | L |
| ボタンが押されている(スイッチON) | 1(真) | H |
確認のために図4の回路図を見ると、プッシュスイッチがOFFの場合は、PRESSED信号は抵抗によりプルダウンされるため、電圧が実際にLになる事が分かります。
また、プッシュスイッチがONの場合は、PRESSED信号はプッシュスイッチを介してVCCに接続されるため、電圧が実際にHになる事が分かります。
一方で、RELEASED信号は、PRESSED信号とは逆に、プッシュスイッチのボタンが押されていない時に真(1)になり、ボタンが押されている時に偽(0)になります。
RELEASED信号も正論理の信号ですから、プッシュスイッチのボタンが押されていない時に電圧がHになり、ボタンが押されている時に電圧がLになります。
これらの事をまとめると、表4の様になります。
| スイッチの状態 | 真理値 | 電圧 |
|---|---|---|
| ボタンが押されていない(スイッチOFF) | 1(真) | H |
| ボタンが押されている(スイッチON) | 0(偽) | L |
表3と表4とを比較すると、PRESSED信号とRELEASED信号は、対立する概念を表現する信号である事が分かります。すなわち、PRESSED信号が0の時はRELEASED信号は1になり、PRESSED信号が1の時はRELEASED信号は0になります。PRESSED信号とRELEASED信号が共に0になったり1になったりする事はありません。
スイッチの状態とPRESSED信号やRELEASED信号の電圧の関係を1つの表で対比できるようにすると、表5の様になります。
| スイッチの状態 | PRESSED信号の電圧 | RELEASED信号の電圧 |
|---|---|---|
| ボタンが押されていない(スイッチOFF) | L | H |
| ボタンが押されている(スイッチON) | H | L |
この表で、「PRESSED信号の電圧」を「X」(NOT回路の入力電圧)と読み替え、「RELEASED信号の電圧」を「Y」(NOT回路の出力電圧)と読み替えると、表2に示したNOT回路の真理値表が得られますから、PRESSED信号をNOT回路に入力すると、RELEASED信号が得られる事が分かります。
この様にして、図4の回路において正しくPRESSED信号からRELEASED信号が得られる事が確認できました。
この例で分かる様に、NOT回路は、ある信号を入力すると、入力信号と対立した概念を表す信号を出力します。NOT回路のこの様な作用を論理反転あるいは論理否定と呼びます。
前節ではNOT回路の入力信号と出力信号が共に正論理の場合を取り上げましたが、入力信号と出力信号が共に負論理の場合も、NOT回路で論理反転が行えます。
図5の様に、プッシュスイッチのボタンが押されている事を表すPRESSEDという負論理の信号をNOT回路に入力して、プッシュスイッチのボタンが押されていない事を表すRELEASEDという負論理の信号を生成する回路について考えます。
PRESSED信号は、プッシュスイッチのボタンが押されていない時に偽(0)になり、ボタンが押されている時に真(1)になります。PRESSEDが負論理の信号である事に注意して、スイッチのボタンが押されていない時と押されている時のPRESSED信号の真理値と電圧の関係を表にすると、表6の様になります。
| スイッチの状態 | 真理値 | 電圧 |
|---|---|---|
| ボタンが押されていない(スイッチOFF) | 0(偽) | H |
| ボタンが押されている(スイッチON) | 1(真) | L |
確認のために図5の回路図を見ると、プッシュスイッチがOFFの場合は、PRESSED信号は抵抗によりプルアップされるため、電圧が実際にHになる事が分かります。
また、プッシュスイッチがONの場合は、PRESSED信号はプッシュスイッチを介してGNDに接続されるため、電圧が実際にLになる事が分かります。
RELEASED信号は、プッシュスイッチのボタンが押されていない時に真(1)になり、ボタンが押されている時に偽(0)になります。RELEASEDが負論理の信号である事に注意して、スイッチのボタンが押されていない時と押されている時のRELEASED信号の真理値と電圧の関係を表にすると、表7の様になります。
| スイッチの状態 | 真理値 | 電圧 |
|---|---|---|
| ボタンが押されていない(スイッチOFF) | 1(真) | L |
| ボタンが押されている(スイッチON) | 0(偽) | H |
表6と表7を見比べると、PRESSED信号がLの場合はRELEASED信号がHになり、PRESSED信号がHの場合はRELEASED信号がLになるので、PRESSED信号をNOT回路に入力すれば、RELEASED信号が得られる事が分かります。
この様に、負論理の回路の場合でも、論理反転(対立する概念を表す信号への変換)ができる事が確認できました。
なお、負論理の回路においてNOT回路で論理反転する場合は、NOT回路の回路記号として図6の記号を使う場合がよくあります。
図6の記号を用いて図5の回路を描き直すと、図7の様になります。
NOT回路を使うと、同じ概念を表す正論理の信号と負論理の信号を変換できます。正論理信号を負論理信号に変換する場合と、負論理信号を正論理信号に変換する場合を、順に説明します。
図8の様に、プッシュスイッチのボタンが押されている事を表すPRESSEDという正論理の信号を、NOT回路を用いて、負論理のPRESSEDという信号に変換する回路について考えます。
PRESSED信号は、スイッチのボタンが押されている事を表す正論理の信号ですから、ボタンが押されていない時に真理値が偽(0)で、電圧がLになり、ボタンが押されている時に真理値が真(1)で、電圧がHになります。
図8の回路図の左側の、プッシュスイッチと抵抗の直列回路により実際にPRESSED信号が得られる事は、図4の回路の場合と同様の考察で理解できます。
一方でPRESSED信号は、PRESSED信号と同様、スイッチのボタンが押されている事を表す信号ではありますが、負論理の信号ですから、ボタンが押されていない時に真理値が偽(0)で、電圧がHになり、ボタンが押されている時に真理値が真(1)で、電圧がLになります。
スイッチの状態と、PRESSED信号やPRESSED信号の真理値や電圧を対比した表が表8です。
| スイッチの状態 | PRESSED | PRESSED | ||
|---|---|---|---|---|
| 真理値 | 電圧 | 真理値 | 電圧 | |
| ボタンが押されていない(スイッチOFF) | 0(偽) | L | 0(偽) | H |
| ボタンが押されている(スイッチON) | 1(真) | H | 1(真) | L |
この表から、PRESSED信号とPRESSED信号とでは、電圧が反対になっている(LとHが入れ替わっている)事が分かります。
よって、図8の回路の様に、正論理のPRESSED信号をNOT回路に入力すれば、負論理のPRESSED信号が得られる事が分かります。
この例から分かる様に、NOT回路には、正論理の信号を、同じ概念を表す負論理の信号に変換する作用があります。
図9の様に、プッシュスイッチのボタンが押されている事を表すPRESSEDという負論理の信号を、NOT回路を用いて、正論理のPRESSEDという信号に変換する回路について考えます。
PRESSED信号は、スイッチのボタンが押されている事を表す負論理の信号ですから、ボタンが押されていない時に真理値が偽(0)で、電圧がHになり、ボタンが押されている時に真理値が真(1)で、電圧がLになります。
図9の回路図の左側の、抵抗とプッシュスイッチの直列回路により実際にPRESSED信号が得られる事は、図5の回路の場合と同様の考察で理解できます。
一方でPRESSED信号は、PRESSED信号と同様に、プッシュスイッチのボタンが押されている事を表す信号ですが、正論理の信号なので、ボタンが押されていない時に真理値が偽(0)で、電圧がLになり、ボタンが押されている時に真理値が真(1)で、電圧がHになります。
スイッチの状態と、PRESSED信号やPRESSED信号の真理値や電圧を対比した表が表9です。
| スイッチの状態 | PRESSED | PRESSED | ||
|---|---|---|---|---|
| 真理値 | 電圧 | 真理値 | 電圧 | |
| ボタンが押されていない(スイッチOFF) | 0(偽) | H | 0(偽) | L |
| ボタンが押されている(スイッチON) | 1(真) | L | 1(真) | H |
注:表8と表9とは、同じ内容を表しています。
この表から、PRESSED信号とPRESSED信号とでは、電圧が反対になっている(LとHが入れ替わっている)事が分かります。
よって、図9の回路の様に、負論理のPRESSED信号をNOT回路に入力すれば、正論理のPRESSED信号が得られる事が分かります。
この例から分かる様に、NOT回路には、負論理の信号を、同じ概念を表す正論理の信号に変換する作用があります。
NOT回路を負論理信号から正論理信号への変換に用いる場合には、図10に示す回路記号を使う事がよくあります。
この回路記号を使って図9を描き直すと、図11の様になります。
次のページでは、NOT回路を含む論理回路の論理圧縮について説明します。
