↑ 画像をクリックすると拡大
図20、UおよびUの部分集合を表したベン図(2入力の場合)
| 2022年05月10日 | 更新 |
AND回路を含む論理回路の働きを、集合論で使うベン図を使って表す事があります。この場合、集合としては、入力信号が取り得る真理値(複数入力の論理回路の場合は入力信号が取り得る真理値の組み合わせ)の集合を考えます。
集合と言っても論理回路ですから、入力信号が取り得る真理値の組み合わせ全ての集合を考えても、要素は多くありません。2入力AND回路の様に入力信号が2本の論理回路の場合、入力信号の真理値の組み合わせは22=4通りしかありません。
具体的に、入力信号が取り得る真理値の組み合わせについて示します。2つの入力信号をAとBとすると、入力信号(A,B)の真理値の組み合わせは、以下の4通りになります。
表記が冗長になるので、前の(A,B)=を省略して書く事にすると、入力信号が取り得る真理値の組み合わせの集合U(全体集合)は、式(21)で与えられます。
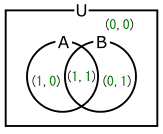
UおよびUの部分集合をベン図で表わすと、図20の様になります。
図20には、分かりやすい様に、Uを構成する4つの要素((0,0)、(0,1)、(1,0)、および(1,1))を書き込んであります。
図20のベン図に出てくる集合Aは、入力信号の組み合わせ(A,B)の中で入力信号Aが1になる物の集合です。具体的には、集合Aは式(22)の様に、(1,0)と(1,1)の2つの要素を持つ集合です。
注意:この説明では、「入力信号A」と「入力信号の組み合わせ(A,B)の中で入力信号Aが1となる物の集合」の両方を同じAという文字で表しています。文字Aがどちらの意味で使われているかは、文脈に依存します。この後に出てくる文字BおよびYも同様です。
また、図20のベン図に出てくる集合Bは、入力信号の組み合わせ(A,B)の中で入力信号Bが1になる物の集合です。具体的には、集合Bは式(23)の様に、(0,1)と(1,1)の2つの要素を持つ集合です。
AとBの2つ入力信号と1つの出力信号Yを持つ2入力AND回路を考えると、出力信号Yは表2の真理値表で与えられます。この真理値表から分かる様に、入力信号の組み合わせ(A,B)の中で出力信号Yが1となる物の集合Yは、(1,1)の1つの要素を持ちます。この事を数式で表わすと式(24)になります。
式(22)～式(24)より、集合Yは集合Aと集合Bの積集合である事が分かります。この事を数式で表わすと式(25)になります。
この様に集合で表わすと、論理積の操作は、積集合を求める操作である事が分かります。(式(1)の論理積の演算子"·"を積集合の演算子"∩"に入れ替えると式(25)になる事に注意してください)
図20のベン図において、出力信号Yが1になる入力信号の組み合わせの集合Yに色を付けて表すと、図21の様になります。
図21のベン図は、2入力AND回路の動作を表す図だと考えられます。このベン図は表2の真理値表と同じ事柄を表していますが、真理値表の様に表形式で表すより、ベン図の様に図形式で表す方が、より直感的に回路動作を把握できます。
なお、3つの信号A、B、およびCを入力して1つの信号Yを出力する3入力AND回路(図4参照)の動作をベン図で表わすと、図22の様になります。
図22のベン図より、3入力AND回路の出力が1になるのは、3つの入力信号A、B、およびCの全てが1になる時だけであると、直感的に分かります。
