↑ 画像をクリックすると拡大
図6、男子生徒の集合Mとピアノを習っている生徒の集合Pを描いたベン図
| 2020年05月26日 | 公開 |
前節では、男子生徒の集合Mを考えましたが、今度はMに加えて、クラスの中でピアノを習っている生徒の集合Pを考えてみます。表1より、集合Pの全要素は式(13)で表せます。
参考:piano(ピアノ)の頭文字を取って、ピアノを習っている生徒の集合をPとしました。
また、Pの補集合、つまりピアノを習っていない生徒の集合Pは、式(14)で表せます。
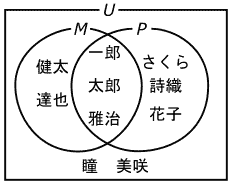
1つのベン図に、男子生徒の集合Mと、ピアノを習っている生徒の集合Pを表すと、図6の様になります。
このベン図を見ると分かる様に、一郎、太郎、雅治の3人は、男子生徒の集合Mと、ピアノを習っている生徒の集合Pの両方に属しています。(3人は、ベン図の中で集合Mを表す線と、集合Pを表す線の両方に囲まれています) この一郎、太郎、雅治の3人からなる集合は集合Mと集合Pの共通部分と呼ばれます。
一般に、集合Aと集合Bのどちらにも属する全ての要素で構成された集合を、AとBの共通部分(intersection)または積集合といい、A∩Bで表します。
注:積集合という言葉は、直積集合の事を指す場合もあります。
AとBとA∩Bの関係をベン図で表すと、図7の様になります。
ピンク色の部分がA∩Bです。
図7のピンク色の部分がA∩Bを表しています。ピンク色の部分は、集合Aの線の内側にも、集合Bの線の内側にも入っている事が分かります。
クラスの生徒の例では、集合Mは男子生徒の集合を表し、集合Pはピアノを習っている生徒の集合を表していますから、それらの共通部分M∩Pは、ピアノを習っている男子生徒の集合になります。M∩Pの全要素を数式で表すと、式(15)になります。
先程挙げた一郎、太郎、雅治の3人は、図6において、集合Mの線の内側にも、集合Pの線の内側にも入っている事が分かります。またMの線の内側にもPの線の内側にも入っている生徒は、一郎、太郎、雅治の3人以外にはいない事が分かります。
またM∩Pは、ピアノを習っていない男子生徒の集合という意味になり、その全要素を数式で表すと、式(16)になります。
図6を見ると、健太と達也の2人は、集合Mの線の内側には入っていますが、集合Pの線の内側には入っていない事が分かります。また、Mの線の内側には入っているものの、Pの線の内側に入っていない生徒は、健太と達也以外にはいない事も分かります。
同様に、M∩Pはピアノを習っている女子生徒の集合という意味になり、またM∩Pはピアノを習っていない女子生徒の集合という意味になります。M∩PとM∩Pの全要素を数式で表すと、それぞれ式(17)と式(18)になります。
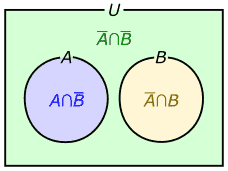
集合Aと集合Bの両方を描いたベン図の中で、A∩B、A∩B、A∩B、およびA∩Bの4つの集合が、どの部分にあたるかを図示すると、一般に図8の様になります。
ただし、集合Aと集合Bの選び方によっては、A∩B、A∩B、A∩B、およびA∩Bの4つの集合の中に、空集合が含まれる事があります。
例えば、A∩B={ }の場合(AとBの共通部分が空集合の場合)、A∩B、A∩B、およびA∩Bの3つの集合の関係をベン図で表すと、図9の様になります。
空集合のA∩Bを描かない事にすると、この様な図になります。この様に空集合を描かない図は、厳密にはベン図ではなくオイラー図というのですが(ベン図は空集合も図に描きます)、オイラー図とベン図を区別せずに、両方をベン図と呼ぶ事もよくあります。この記事では、オイラー図の事もベン図と呼びます。
他の例として、A∩B={ }の場合のA∩B、A∩B、およびA∩Bの関係をベン図で表すと、図10の様になります。
A∩B={ }の場合は、AとBが包含関係になります。
ところで一般に、集合Aと集合Bの少なくともどちらか一方に属する全ての物で構成された集合を、AとBの和集合(union)といい、A∪Bで表します。
AとBとA∪Bの関係をベン図で表すと、図11の様になります。
A∩B、A∩B、A∩B、およびA∩Bの4つの集合の全てが、空集合でない事を仮定して作図しています。
クラスの生徒の例で考えてみます。男子生徒の集合Mとピアノを習っている生徒の集合Pの和集合、M∪Pの要素を数式で表すと、式(19)になります。
式(19)に出てくる8人は全員、集合Mか集合Pの少なくとも一方に属しており、また集合Mか集合Pの少なくとも一方に属している生徒は、式(19)に出てくる8人以外にいない事が図6で確認できます。
A∪Bが図11の様なベン図で表されると先程説明しましたが、これは、A∩B、A∩B、A∩B、およびA∩Bの4つの集合の全てが、空集合でない場合の話です。
A∩B={ }の場合を考えると、A∪Bは、図12に示す集合になります。
ピンク色の部分がA∪Bです。
図12では、集合Aと集合Bが接する様に描かれていますが、もし、図9の様に、AとBを離して描くと、A∪Bが2つの領域に分かれてしまう事に注意が必要です。
注:A∪Bが2つの領域に分かれてしまった図を描いても、間違いという訳ではありません。
またA∩B={ }の場合は、図13に示す様にAがBの部分集合になり、A∪B=Bとなります。
ピンク色の部分がA∪Bです。
図11の様に、A∩B、A∩B、A∩B、およびA∩Bの4つの集合が全て空集合ではない場合、A∪B、A∪B、およびA∪Bをベン図で示すと、それぞれ図14、図15、および図16になります。
ピンク色の部分がA∪Bです。
ピンク色の部分がA∪Bです。
ピンク色の部分がA∪Bです。
なお、図16と図7とを見比べると、A∪Bは、A∩Bの補集合(A∩B)と等しい事が分かります。この事から示される式(20)の関係は、ド・モルガンの法則と呼ばれています。
ピンク色の部分がA∩Bです。
次のページでは、扱う集合が3つ以上の場合のベン図について説明します。
