| 2022年04月22日 | 更新。 |
真理値(truth value)または論理値(logical value)とは、命題の真偽を表す値の事です。命題が正しい事を表している場合は、その命題の真理値は真(true)となり、命題が正しくない事を表している場合は、その命題の真理値は偽(false)となります。
古典的な論理学において真理値は真または偽の値を取ります。この様に、真または偽の2種類の真理値のみを扱う論理の事を2値論理といいます。
一方で、真と偽以外にも、例えば「真か偽か分からない」状態を表す真理値を設けるなど、3種類以上の真理値を考える事があります。この様な論理を多値論理といいます。
まず2値論理について簡単に説明し、次に2値論理と2値論理回路の関係について説明します。
命題の例と、その命題の真理値を、表1に示します。
| 命題 | 真理値 |
|---|---|
| 富士山は日本で一番高い山だ。 | 真 |
| 富士山は日本で2番目に高い山だ。 | 偽 |
| xを実数とする時、x<x+1が成立する。 | 真 |
| xを実数とする時、x>x+1が成立する。 | 偽 |
| xを実数とする時、x>5ならばx>25が成立する。 | 真 |
| 犬は動物だ。 | 真 |
| 人間は爬虫類だ。 | 偽 |
論理学では、真の事をT、偽の事をFで表す事が多くあります。また電子工学では、真の事を1、偽の事を0で表す事が多くあります。
電子工学の場合、真理値の0と1は、2進数の1桁(1ビット)の値の0と1と同一視される事がしばしばあります。
真理値を2値論理回路内の電圧に対応させる時に、真を高い電圧のHに、偽を低い電圧のLに対応させる事が多いですが、この対応を正論理といいます。場合によっては真をLに、偽をHに対応させる事もありますが、この対応を負論理と呼びます。
電子工学の分野で、多値論理がどの様に使われているかを説明します。
最初に説明したとおり、真と偽以外にも真理値を考えるのが多値論理です。多値論理には色々な形式が考えられますが、ここでは、真と偽以外に「真か偽か分からない」という真理値を考える3値論理について考えます。
「真か偽か分からない」という真理値の事を、電子工学の分野ではしばしば不定値(あるいは単に不定)と呼びます。不定値は英訳するとunknown value(あるいはundefined value)になりますので、Uの記号で表す事があります。(後述するDon't careと区別せずに、不定値をXの記号で表す事もありますが、この記事では不定値をUの記号で表す事にします)
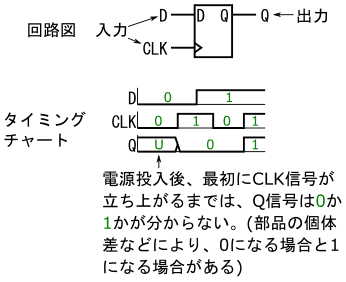
2値論理回路において不定値は、例えばユーザーのボタン操作により真理値が変わる信号線で、ユーザーがどの様な操作をしているかが分からない場合や、電源投入後、まだリセット信号やクロック信号を入力していないDフリップフロップの出力信号等で発生します。(図1参照)
実際の2値論理回路の信号線の電圧を測った場合、電圧が低ければ真理値は0(偽)、電圧が高ければ真理値は1(真)になるので(ただし正論理の場合)、実際の回路においては真理値は0または1のいずれかの値になります。しかし、思考実験(シミュレーション)で回路の動作を考える時には、図1に示す様に、不定値を扱う必要が出てくるのです。
次に、図2に示す、2入力のAND回路に付いて考えます。
2値論理で考えると、2入力AND回路の真理値表は表2の様になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
同じ2入力AND回路の真理値表を、不定値を含む3値論理で考えると、表3の様になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | U | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | U | U |
| U | 0 | 0 |
| U | 1 | U |
| U | U | U |
表3を見ると、A=0でB=Uの場合に、Y=0になっています。この様に、入力に不定値を含む場合でも、出力が0が1のどちらかに確定する場合があります。
今度は、真と偽に、「真と偽のどちらでも良い」という真理値を加えた3値論理について考えます。
「真と偽のどちらでも良い」という真理値を、電子工学ではしばしばDon't care(ドントケア)と呼びます。
Don't careを表す記号には、X、D、−、⌀等が使われますが、この記事ではXでDon't careを表す事にします。
Don't careの説明のために、図3に示す2入力のOR回路について考えます。
0と1の2値論理で考えると、2入力OR回路の真理値表は表4の様になります。
| 入力 | 出力 | 備考 | |
|---|---|---|---|
| A | B | Y | |
| 0 | 0 | 0 | 1行目 |
| 0 | 1 | 1 | 2行目 |
| 1 | 0 | 1 | 3行目 |
| 1 | 1 | 1 | 4行目 |
Don't care(X)を使うと、表4は、表5の様に簡略化できます。
| 入力 | 出力 | 備考 | |
|---|---|---|---|
| A | B | Y | |
| 0 | 0 | 0 | 1行目 |
| 0 | 1 | 1 | 2行目 |
| 1 | X | 1 | 3行目 |
この様に、Don't careを使うと、元々は4行の表を3行で表せる事が分かります。Xは0でも1でもいいのですから、表5の3行目は、表4の3行目と4行目の情報を1行で表したものになります。
2入力OR回路の場合は4行が3行になる程度の効果でしたが、図4に示すもっと複雑な回路では、真理値表が8行(表6参照)から4行(表7参照)へと、半分に減ります。
| 入力 | 出力 | ||
|---|---|---|---|
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| 入力 | 出力 | ||
|---|---|---|---|
| A | B | C | Y |
| 0 | X | X | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | X | 1 |
表5や表7の様に、真理値表の入力信号の欄にDon't careを使ったのは、真理値表を簡潔に表すためでした。大きな真理値表を書くのが嫌でなければ、別にDon't careを使わなくてもいい訳です。
今度は、真理値表の出力信号の欄にDon't careを使う話をします。この場合、表の簡略化とは違う効果が出ます。
ASIC、FPGA、PLD等の論理設計をする際に、欲しい回路の真理値表を入力して、その真理値表通りに動作する論理回路を、コンピュータに自動生成させる事があります。今、表8の様に、出力信号にDon't careを含む真理値表を与えて、コンピュータに論理回路を自動生成させる事を考えます。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | X |
この表では、AとBの両方に1を入力する時の出力がXになっています。これは、AとBの両方に1を入力する際に、0を出力する回路を作ってもいいし、1を出力する回路を作ってもいい事を表しています。(出力が不定になる訳ではありません)
この様な要求仕様は、例えばAとBに、同時には1が入力されない事が保証されている回路で発生する事があります。
AとBの両方に1を入力する際に0を出力する回路を生成する場合は、表9の真理値表に基づいて、図5に示すXOR回路を生成する事になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
一方で、AとBの両方に1を入力する際に1を出力する回路を生成する場合は、表10の真理値表に基づいて、図6に示すOR回路を生成する事になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
表9や表10の様に、Don't careを含まない自由度の低い真理値表を指定する場合は、コンピュータが生成できる回路が1種類しかありませんが、表8の様に、出力信号にDon’t careを含む自由度の高い真理値表を指定する場合は、コンピュータが複数の回路を生成でき、それらの中から最も性能の良い(動作速度が速い、使用部品が少ない等の)回路を選ぶ事ができます。
