「ベン図」の解説(1)
このページをスマートフォンなどでご覧になる場合は、画面を横長にする方が読みやすくなる事があります。
ベン図(Venn diagram)とは、集合の範囲を視覚的に表すために用いる図の事です。考案したの数学者のジョン・ベンの名前にちなんでベン図と名付けられました。
ベン図は集合の要素が存在する範囲を、線で囲んで表します。集合の要素は、その線の内側に書きます。複数の集合に属する要素は、属する全ての集合の線の内側に書きます。(図1参照)
複数の集合を扱う場合、ベン図を使うと、集合の関係が直観的に理解できます。ただし、4つ以上の集合を扱う場合は、ベン図が複雑になり、集合の関係が直観的に理解できなくなって、ベン図の利点が薄れるため、1~3個の集合をベン図に表す事が一般的です。
ベン図は集合以外の分野にも応用が可能です。電子工学の分野では、1~3変数の論理関数や、1~3入力1出力の組み合わせ回路(2値論理回路の一種)の真理値表を、視覚的に表現するためにベン図が用いられます。
↑ 画像をクリックすると拡大
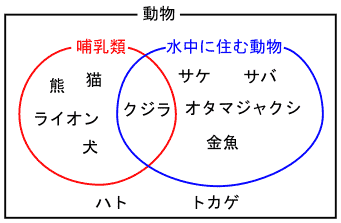
図1、哺乳類の集合と水中に住む動物の集合の関係を表したベン図
猫と熊とライオンと犬は、哺乳類ですが、水中に住む動物ではありません。そのため、これらの動物は哺乳類の集合の範囲を示す赤い線に囲まれていますが、水中に住む動物の集合を表す青い線には囲まれていません。
サケとサバとオタマジャクシと金魚は、水中に住む動物ですが、哺乳類ではありません。そのため、これらの動物は、青い線に囲まれていますが、赤い線には囲まれていません。
クジラは哺乳類でもありますし、水中に住む動物でもあります。そのため、クジラは赤い線と青い線の両方に囲まれています。
ハトとトカゲは、哺乳類でも水中に住む動物でもありません。そのため、これらの動物は、赤い線にも青い線にも囲まれていません。
この例の様に、ベン図を書くと、各対象物がどの集合に属するのか、属さないのかといった事が視覚的に理解できます。また、上のベン図からは、哺乳類の集合と水中に住む動物の集合が共通部分(クジラからなる集合)を持つことも、直観的に理解できます。
目次
1.集合論におけるベン図
この章では、まず集合論で使われるいくつかの言葉や記号の意味について確認します。
次に、ベン図が集合の範囲を示す図であり、ベン図を使うと複数の集合の関係を視覚的に表せる事を、扱う集合の数が1つの場合、2つの場合、3つの場合、および4つ以上の場合に分けて、簡単な例を挙げながら説明します。
1-1.集合に関する用語や記号の説明
1-1-1.集合
数学において集合(set)とは、物の集まりの事を指します。ただし、その議論で扱う物が、その集合に属するかどうかが明確に判断できなければなりません。
例えば、3以下の自然数の集まりなら集合といえますが、英語の得意な日本人の集まりは集合とはいえません。(ある人が、英語が得意といえるかどうかは、主観によるため)
集合はどんな物の集まりでもいいのですが、多くの場合、何らかの共通の性質を持った物の集合を問題にします。
1-1-2.有限集合、無限集合、空集合
集合を構成する物の個数は、有限個でも、無数にあっても構いません。
集合を構成する物の個数が有限個の場合、その集合を有限集合(finite set)と呼びます。特に、構成する物の個数が0個の集合(これも有限集合の一種と考える)を空集合(empty set)と呼び、{ }や∅で表します。
集合を構成する物の個数が無限の集合を、無限集合(infinite set)と呼びます。
具体的な例を挙げると、有限集合の例としては、例えば京都に住んでいる人の集合や、10以下の自然数の集合があります。また、空集合の例としては、例えば500歳以上の人の集合や、2乗すると負の数になる自然数の集合があります。無限集合の例としては、例えば整数の集合や、全ての数式の集合があります。
1-1-3.要素(元)
集合を構成する個々の物を要素、または元といいます。
集合論で変数を使う場合、集合を表す変数には大文字(AやX等)を使い、要素を表す変数には小文字(aやx等)を使う習慣があります。
xが集合Aの要素である事は、式(1)で表現します。
x ∈ A ··· (1)
例えば、偶数の集合をEとすると、2という数はEの要素なので、式(2)の様に表現できます。
2 ∈ E ··· (2)
xが集合Aの要素ではない事は、式(3)で表現します。
x ∉ A ··· (3)
例えば、3という数は、偶数の集合Eの要素ではないため、式(4)の様に表現できます。
3 ∉ E ··· (4)
x∈Aの関係は、「xはAの要素である」といういい方もしますが、「xはAに属する」とか、「Aはxを含む」という事もあります。
1-1-4.全ての要素を書き出す事により集合を定義する方法
有限集合の場合、その集合の全ての要素が共通して持っている性質により定義する事以外にも、全ての要素を書き出す事でも定義できます。要素を書き出して集合を表すには、全ての要素をカンマ(,)で区切り、それらの要素を波括弧でくくります。
例えば、3以下の自然数の集合をTとすると、Tを「3以下の自然数の集合」と定義するのは、Tの要素が共通して持っている性質を用いた定義の仕方といえます。
一方で、Tを、Tの全ての要素を書き出して定義するなら、式(5)の様になります。
T = { 1, 2, 3 } ··· (5)
式(5)は、1と2と3がTの要素である事と、1と2と3以外にはTの要素はない事を表しています。
参考:空集合を{ }で表すのは、波括弧の中に書く要素がないからです。
1-2.扱う集合が1つの場合
今、ある学校のあるクラスの生徒について考える事にします。そのクラスの生徒は全部で10人で、生徒の名前は、一郎、健太、さくら、詩織、達也、太郎、花子、瞳、雅治、美咲です。また、各生徒のプロフィールを表1に示します。
表1、各生徒のプロフィール
| 名前 |
プロフィール |
| 一郎 |
男の子。ピアノを習っている。サッカーが好き。 |
| 健太 |
男の子。ピアノは習っていない。サッカーが好き。 |
| さくら |
女の子。ピアノを習っている。サッカーが好き。 |
| 詩織 |
女の子。ピアノを習っている。サッカーに興味はない。 |
| 達也 |
男の子。ピアノは習っていない。サッカーに興味はない。 |
| 太郎 |
男の子。ピアノを習っている。サッカーに興味はない。 |
| 花子 |
女の子。ピアノを習っている。サッカーに興味はない。 |
| 瞳 |
女の子。ピアノは習っていない。サッカーに興味はない。 |
| 雅治 |
男の子。ピアノを習っている。サッカーが好き。 |
| 美咲 |
女の子。ピアノは習っていない。サッカーが好き。 |
考える対象全体の集合を全体集合(universal set)といいます。
今、クラスの生徒について考えているので、クラスの生徒の集合が全体集合です。その全体集合をUとすると、Uは式(6)で表されます。
U = { 一郎, 健太, さくら, 詩織, 達也, 太郎, 花子, 瞳, 雅治, 美咲 } ··· (6)
式(6)の全体集合Uをベン図に描くと、図2の様になります。
↑ 画像をクリックすると拡大
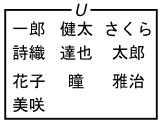
図2、全体集合Uの要素を表すベン図
ベン図では、図2の様に集合を閉じた線で表し、集合の要素は、その閉じた線の内側に書きます。
次に、Uの部分集合について考えます。
部分集合(subset)とは、その集合の全ての要素が、他の集合の要素になっているような集合の事です。集合Aの全ての要素が集合Bの要素である時、「AはBの部分集合である」といい、式(7)の数式で表します。
A ⊆ B ··· (7)
AがBの部分集合の時、「BはAの上位集合(superset)である」ともいいます。
また、2つの集合があり、一方の集合が他方の集合の部分集合であるような関係を、包含関係といいます。
クラスの生徒の例で考えてみまます。例えばクラスの男子生徒の集合をMとすると、MはUの部分集合になります。また、UはMの上位集合です。
参考:男性の事は英語でmaleといいますので、男子生徒の集合を、maleの頭文字を取ってMとしました。
集合Mの全要素を数式で表すと、式(8)の様になります。
M = { 一郎, 健太, 達也, 太郎, 雅治 } ··· (8)
Mの要素(一郎、健太、達也、太郎、および雅治の5人)が全てUの要素になっている事から、MがUの部分集合になっている事が確認できます。これを数式で表現すると式(9)になります。
M ⊆ U ··· (9)
ところで、集合Aが集合Bの部分集合である場合には、2つのケースが考えられます。
1つ目のケースは、集合Aと集合Bが同じ集合である場合です。もう1つのケースは、Bの要素の一部がAの要素になっている場合(Bの要素ではあるがAの要素ではない物が存在する場合)です。
後者の、Bの要素の一部がAの要素になっている場合に、AはBの真部分集合といい、この関係を式(10)で表します。
A ⊂ B ··· (10)
注:この記事ではAがBの部分集合である事をA⊆Bで表し、AがBの真部分集合である事をA⊂Bで表していますが、AがBの部分集合である事をA⊂Bで表し、AがBの部分集合である事をA⊊Bで表す流儀もあります。"⊂"の記号が真部分集合を表しているのか、部分集合を表しているのかは、どちらの流儀を採用しているかによります。
例えば、男子生徒の集合Mは、全体集合Uの要素の全部ではなく、一部から構成されていますから、MはUの真部分集合です。よって、式(11)の数式が成立します。
M ⊂ U ··· (11)
参考:真部分集合は部分集合の一種なので、式(9)と式(11)は矛盾しません。
全体集合Uと、その真部分集合であるMをベン図に描くと、図3の様になります。
↑ 画像をクリックすると拡大
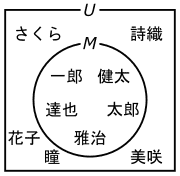
図3、全体集合Uと男子生徒の集合Mの関係
Mの要素である一郎、健太、達也、太郎、雅治の5人はMを表す線の内側に書きますが、Mの要素ではない、さくら、詩織、花子、瞳、美咲の5人は、Mを表す線の外側に書きます。
ところで図3を見ると、男子生徒の集合Mが、上位集合のUに囲まれている事が分かります。
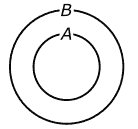
一般に、集合Aが集合Bの真部分集合である場合、図4に示す様に、ベン図上ではAがBに囲まれた形となります。
注:厳密には、図4の図は、ベン図とは呼ばずにオイラー図と呼びますが、ベン図もオイラー図も区別せずに、まとめてベン図と呼ぶ事も多くあります。この記事では、オイラー図の事もベン図と呼ぶ事にします。
↑ 画像をクリックすると拡大
図4、集合Aが集合Bの真部分集合である場合のベン図
なお、全ての集合は全体集合の部分集合ですから、全体集合そのものを除く他の集合は、ベン図上では全体集合に囲まれた形になります。
ところで、全体集合から、集合Aの要素を取り除いて得られる集合を、Aの補集合(complement)といい、Aで表します。
一般に、ベン図において補集合の要素は、図5の様に集合を表す線の外側に書かれます。

↑ 画像をクリックすると拡大
図5、集合Aの補集合
ピンク色の部分が、Aの補集合であるAです。またUは、全体集合です。
Aの要素は、ピンク色の部分に記入します。
図3を見ると、さくら、詩織、花子、瞳、美咲の5人が集合Mの線の外側に書かれていますから、これらのメンバーで構成される集合(女子生徒の集合)がMという事になります。Mの全要素を数式で表すと、式(12)の様になります。
M = { さくら, 詩織, 花子, 瞳, 美咲 } ··· (12)
次のページでは、扱う集合が2つの場合のベン図について説明します。
関連用語
関連ページ

このサイトの記事が本になりました
本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。

このサイトの中の人が書いた本です。
本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。







