図の中に書いてある3桁の数字は、左の桁から順に、集合Mに属するか、集合Pに属するか、集合Sに属するかを表す真理値です。
| 2020年06月06日 | 公開 |
前章ではベン図が集合論で使われる事を説明しました。
ベン図は、本来は集合論で使われる図なのですが、集合論と論理関数の間には、ある類似性が存在します。その類似性のため、ベン図は論理関数の理解や、論理関数の計算をする組み合わせ回路(2値論理回路の一種)の動作の理解のためにも利用できます。
この章では、論理関数や論理回路で用いられるベン図について説明します。
前章では、表1に示す10人の生徒の集合を例に、集合論におけるベン図について説明しました。
表1は、表4の様に要約できます。
| 名前 | Mに属するか | Pに属するか | Sに属するか |
|---|---|---|---|
| 一郎 | 1 | 1 | 1 |
| 健太 | 1 | 0 | 1 |
| さくら | 0 | 1 | 1 |
| 詩織 | 0 | 1 | 0 |
| 達也 | 1 | 0 | 0 |
| 太郎 | 1 | 1 | 0 |
| 花子 | 0 | 1 | 0 |
| 瞳 | 0 | 0 | 0 |
| 雅治 | 1 | 1 | 1 |
| 美咲 | 0 | 0 | 1 |
表4の一番左側の列には、生徒の名前が書いてあります。
表4の2~4列目には、それぞれ、集合M、集合P、集合Sに属するかどうかが、0または1で書かれています。0の場合はその集合に属さない事を、1の場合はその集合に属する事を表しています。この0と1は、「その人は集合X(XにはA~Cのいずれかが入る)に属する」という命題の真理値になっている事に注意してください。(0が偽で1が真です)
各集合がどの様な集合であったかを振り返っておきます。Mは男子生徒の集合でした。Pはピアノを習っている生徒の集合でした。Sはサッカーが好きな生徒の集合でした。
例えば表4で詩織の行を見ると、左から0、1、0となっています。つまり、詩織はMには属さず、Pには属して、Sには属さない生徒という事になります。さらに分かりやすくいうと、詩織は女子生徒で、ピアノを習っていて、サッカーに興味がないという事になります。(これは、表1の説明と一致しています)
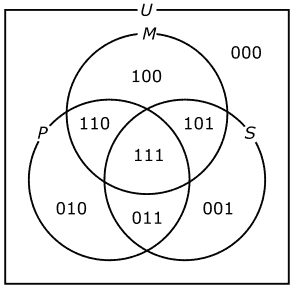
表4の例で分かる様に、(全体集合Uの)各要素は、各集合に属するかどうかの真理値で、ベン図上のどの領域に属するかが決まります。(図23参照)

図の中に書いてある3桁の数字は、左の桁から順に、集合Mに属するか、集合Pに属するか、集合Sに属するかを表す真理値です。
表4の場合はM、P、Sの3つの集合を問題にしていたので、各要素の属性を表す真理値は3つでしたが、一般にN個(N=1,2,3···)の集合を問題にする場合は、N個の真理値で、各要素の属性が表現できます。
あるいは、真理値と2進数1桁の数字を同一視するなら、N個の集合を問題にする場合、N桁の(Nビットの)2進数で、各要素の属性が表現できるという事もできます。
注:「2進数」という用語は、「二進法で表記した数」という意味で使っています。数学におけるp進数の、p=2の場合を指している訳ではありません。
この様に、集合論における物の属性は、集合の数と同じビット数の2進数で表現できるために、論理関数や論理回路と関連付けて考える事ができます。
論理関数の議論でベン図がどの様に使われるかを説明するため、今、2変数の論理関数F(A,B)を考えます。
論理関数(ブール関数)というのは真理値の変数(0か1の値を取る変数)を取り、関数の計算値も真理値になる様な関数の事です。2つの変数AとBを取る論理関数F(A,B)の場合は、AとBとF(A,B)が、0(偽)または1(真)の値を取ります。
あまり抽象的な話をすると、話が理解しにくくなるため、例として、論理関数Fは論理和だとして、論理和のベン図の描き方について考えます。この場合、論理関数Fは式(23)で表されます。
この時、論理関数F(A,B)を真理値表で表すと、表5の様になります。
| A | B | F(A,B) (=A+B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
ここで、2つの変数AとBの値の、組み合わせについて考えます。
例えばAの値が0でBの値が1の組み合わせが考えられます。この組み合わせを、省略して(A,B)=(0,1)と表記する事にします。(Aの値が1でBの値が0なら、(A,B)=(1,0)です)
さらに、2つの変数がAとBだと分かっている場合は、(A,B)=(0,1)の最初の(A,B)=の部分を省略して、(0,1)と書いてもいい事にします。
この表記法を使って書くと、AとBの値の、考えられる組み合わせは、(0,0)、(0,1)、(1,0)、および(1,1)の4つとなります。
ここで、変数Aと変数Bの値の、考えられる全ての組み合わせ、すなわち、先程示した(0,0)、(0,1)、(1,0)、および(1,1)の4つを要素とする集合を、全体集合Uとして、集合の議論をします。
全体集合Uの定義を数式で書くと、式(24)になります。
また、変数Aと変数Bの値の組み合わせの内、変数Aの値が1となる物の集合を、集合Aとします。
ここで、変数Aと集合Aは、互いに密接に関係しているために、同じ名前Aを用いています。単にAと書くと、変数を指すのか集合を指すのかが分かりにくいため、これ以降は、「変数A」や「集合A」と呼び、変数と集合を区別する事にします。
集合Aは、変数Aと変数Bの値の組み合わせの内、変数Aの値が1となる物の集合ですから、式(25)で与えられます。
また、変数Aと変数Bの値の組み合わせの内、変数Bの値が1となる物の集合を、集合Bとします。この時集合Bは、式(26)で与えられます。
全体集合Uと集合Aと集合Bの関係をベン図で表すと、図24の様になります。
図24の外側の長方形は、全体集合Uを表しています。論理関数のベン図の場合、全体集合の変数名Uは、通常記載しません。
またこの図には、全体集合Uを構成する4つの要素、(0,0)、(0,1)、(1,0)、および(1,1)も書き込んであります。この図に示す様に、論理関数の議論で使うベン図の場合、集合Aの範囲を示す円と集合Bの範囲を示す円とで区切られた4つの領域に、要素が1つずつ入ります。
(1,0)と(1,1)は、変数Aの値が1になる組み合わせですから、集合Aの範囲を表す円の内側に書いてあります。また(0,0)と(0,1)は、変数Aの値が0になる組み合わせですから、集合Aの範囲を表す円の外側に書いてあります。
同様に、(0,1)と(1,1)は、変数Bの値が1になる組み合わせですから、集合Bの範囲を表す円の内側に書いてあります。また(0,0)と(1,0)は、変数Bの値が0になる組み合わせですから、集合Bの範囲を表す円の外側に書いてあります。
図24のベン図において、論理関数F(A,B)の値が1になる範囲をピンクに着色したのが図25です。
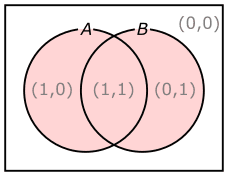
この図には、(0,0)等の変数Aと変数Bの値の組み合わせが灰色で書き込んでありますが、これらは、表5の真理値表との対応を見やすくするために書き込んだものです。論理関数のベン図には、これらの変数の値の組み合わせが書かれていなくても構いません。
図25と表5を見比べると、真理値表でF(A,B)の欄が1になっている変数Aと変数Bの値の組み合わせだけが、ベン図上でピンク色に着色されている事が理解できると思います。
図25の様に、論理関数F(A,B)の値が1になる範囲を着色して表したベン図の事を、単に「論理関数F(A,B)のベン図」といいます。
今回は論理関数F(A,B)の真理値表(表5)が先に分かっていて、そこから図25のベン図を求めましたが、逆に図25のベン図から、表5の真理値表を求める事もできます。言い換えると、ベン図と真理値表は1対1対応しています。この様に、ベン図は真理値表を視覚的に表した図だという事がいえます。
図25が論理和の真理値表を視覚的に表した図だという事は、図25は、論理和演算を行なうOR回路(図26参照)の真理値表を視覚的に表した図だともいえます。
論理回路の真理値表を表現したベン図の事を、単に「論理回路のベン図」といいます。(図25の場合は、2入力OR回路のベン図です)
ところで、図25から分かる通り、論理和の演算(OR演算)は、ベン図上では和集合を求める事に相当します。論理和も、和集合も、「和」という言葉が付きますから、憶えやすいと思います。
次に、別の2変数論理関数として、式(27)に示す論理積演算について考えます。
G(A,B)の真理値表を、表6に示します。
| A | B | G(A,B) (=A·B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
この真理値表を基に、論理積のベン図を作成すると、図27の様になります。
図27は、図28に示す2入力AND回路のベン図でもあります。
図27を見ると分かる様に、論理積の演算(AND演算)は、ベン図上では積集合(共通部分)を求める事に相当します。論理積も、積集合も、「積」という言葉が付きますから、憶えやすいと思います。
先程は2変数の論理関数の議論で使われるベン図について説明しましたが、今度は1変数の論理関数の議論で使われるベン図について説明します。
変数Aを取る、1変数の論理関数、F(A)を考えます。
変数Aの考えられる値の組み合わせ(組み合わせといっても1変数しかないので実質は変数Aの値)は、(A)=(0)と(A)=(1)の2つです。
そこで、全体関数Uを式(28)の様に定義して、集合の議論をします。
全体集合Uの2つの要素の内、変数Aの値が1になる物の集合を集合Aとすると、集合Aは式(29)で与えられます。
全体集合Uと変数Aの関係をベン図に表すと、図29の様になります。
1変数の論理関数F(A)の例として、式(30)の論理否定関数を考えます。
この場合、変数Aの値が0の時に論理関数F(A)の値が1になりますから、論理関数F(A)を表すベン図(論理式Aを表すベン図)は、図30に示す様に、集合Aの外側を着色したものになります。
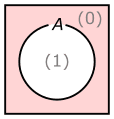
この図には、(0)と(1)が灰色で書き込んでありますが、これらは、図が解釈しやすい様に、その領域での変数Aの真理値を書き込んであるだけです。論理関数のベン図には、(0)や(1)が書かれていなくても構いません。
この様に、論理否定演算(NOT演算)は、ベン図上では補集合を求める事に相当します。変数Aの論理否定を表す論理式はAと記述しますし、集合Aの補集合もAと記述します。論理式でも集合でも同じ記号を使うので、憶えやすいと思います。
また、図31に示すNOT回路は、論理式Aを計算する回路ですから、図30のベン図は、NOT回路の動作を表したベン図でもあります。
この項では、3変数の論理関数のベン図について説明します。
3変数の論理関数F(A,B,C)を考えます。
3つの変数A、B、Cの値の考えられる組み合わせは、(A,B,C)=(0,0,0)、(0,0,1)、(0,1,0)、···、(1,1,1)と、8通り考えられます。
ここで、それら8通りの組み合わせの集合を、全体集合Uとして、集合の議論をします。全体集合Uは、式(31)で定義されます。
全体集合Uの要素の中で、変数Aの値が1になる物の集合を集合Aとすると、集合Aは式(32)で与えられます。
全体集合Uの要素の中で、変数Bの値が1になる物の集合を集合Bとすると、集合Bは式(33)で与えられます。
全体集合Uの要素の中で、変数Cの値が1になる物の集合を集合Cとすると、集合Cは式(34)で与えられます。
全体集合Uと集合A集合Bと集合Cの関係をベン図で表すと、図32の様になります。
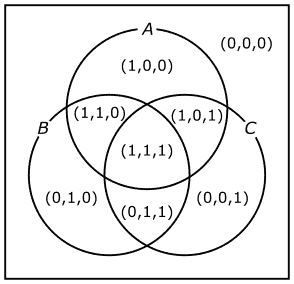
この外側の正方形が全体集合Uを表しています。
このベン図は、図23のベン図とほぼ同じです。図23は、クラスの生徒を分類したベン図であり、論理関数の議論とは全く関係ないにも関わらず、3変数の論理関数の議論で扱うベン図と、形式上は同じ形をしています。
3変数の論理関数の具体的な例として、式(35)の関数を考えてみます。
式(35)の論理関数の真理値表を表7に示します。
| A | B | C | F(A,B,C) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
表7の真理値表で、F(A,B,C)の値が1になっている行の変数A、変数B、変数Cの組み合わせについて、図32のベン図の対応部分に着色をすると、図33の様なベン図ができます。これが、式(35)の論理関数のベン図です。
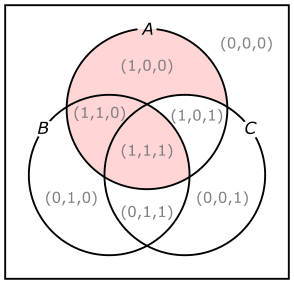
この図には、(0,0,0)等の変数A、変数B、および変数Cの値の組み合わせが灰色で書き込んでありますが、これらは、表7の真理値表との対応を見やすくするために書き込んだものです。論理関数のベン図には、これらの変数の値の組み合わせが書かれていなくても構いません。
表7の真理値表と図33のベン図は、同じ情報を表していますが、ベン図の方が、関数値が1となる変数の組み合わせの範囲が、視覚的に把握しやすくなっています。
例えば、変数Aの値が1になる事は、論理式A·(B+C)の値が1になる事の必要条件ですが、図33のベン図を見ると、ピンク色に着色された領域は全て、確かに集合Aの円の内部になっています。また、変数Bの値が1になるか、または変数Cの値が0になる事も、論理式A·(B+C)の値が1になる事の必要条件ですが、図33のベン図を見ると、ピンク色に着色された領域は全て、確かに集合Bの円の内部であるか、または集合Cの円の外部になっています。この様に、ベン図を使えば、論理関数を視覚的に把握できます。
ところで図34に示す回路は、論理式A·(B+C)の値を計算するための論理回路です。よって、図33のベン図は、図34の論理回路の動作を表したベン図でもあります。
