「ベン図」の解説(3)

1-4.扱う集合が3つの場合

前節では、男子生徒の集合Mとピアノを習っている生徒の集合Pについて考えましたが、この節では、サッカーが好きな生徒の集合Sについても考える事にします。

参考:サッカーを意味する英単語soccerの頭文字を取って、サッカーが好きな生徒の集合をSとしました。

表1を見れば分かる様に、サッカーが好きな生徒の集合Sと、サッカーに興味がない生徒の集合Sを構成する要素は、それぞれ式(21)と式(22)の様になります。

クラスの生徒全員の集合Uの要素を、Mに属しているか、Pに属しているか、そしてSに属しているかの3つの観点で分類すると、2³=8通りに分類できます。クラスの全生徒の分類結果を、表2に示します。

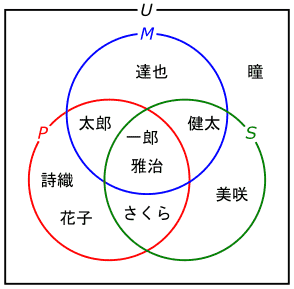
表2に基づいて、M、P、Sの3つの集合を同時に描いたベン図は、図17の様になります。

↑ 画像をクリックすると拡大

図17、M、P、Sの集合を同時に描いたベン図

図17を見ると、生徒のプロフィールが、表1よりも直観的に把握しやすくなっているのが分かります。

例えば、サッカーに興味がない男子生徒を探そうとすれば、表1の場合、生徒のプロフィールを順に読んでいく必要があります。一方でベン図なら、図18に示した様に、サッカーが好きな生徒の集合Sを示す緑色の円の外側に書かれていて、男子生徒の集合Mを示す青色の円の内側に書かれている生徒を探せばよく、達也と太郎の2人が該当する事が、視覚的に把握できます。

↑ 画像をクリックすると拡大

図18、サッカーに興味がない男子生徒をベン図上で探す例

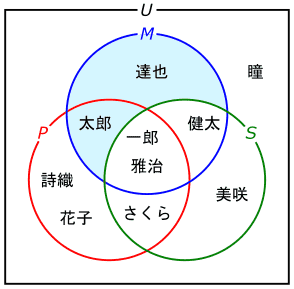
集合Sの範囲を示す緑色の円の外側で、かつ集合Mの範囲を示す青色の円の内側の領域(M∩S)を水色で着色しました。着色した範囲には、達也と太郎の2人の名前があります。

一般に、3つの集合A、B、Cを1つのベン図に書くと、図19の様になります。

↑ 画像をクリックすると拡大

図19、3つの集合を描いたベン図

このベン図には、3つの円で区切られた8つの領域が、それぞれ何の集合であるかを数式で書いてあります。3つの集合A、B、およびCの選び方によっては、これらの領域の中に、空集合になる領域が生じる事があります。

1-5.扱う集合が4つ以上の場合

4つの集合A、B、C、およびDを1つのベン図に描くとどうなるかを考えてみましょう。

図19の3つの集合のベン図から類推して、図20に示す様なベン図になると想像する人がいるかも知れません。しかし、このベン図では不完全なのです。

↑ 画像をクリックすると拡大

図20、3つの集合のベン図から類推して作成した、4つの集合の不完全なベン図

図20には、A～Cの集合の範囲を表す4つの円で区切られた領域に、灰色で数字を書いておきました。この数字を見ると分かる様に、図20では、全体集合Uが14個の領域に分けられている事が分かります。

しかし、Uの要素は、集合Aに属しているかどうか、集合Bに属しているかどうか、集合Cに属しているかどうか、集合Dに属しているかどうかで、2⁴=16種類に分類されるはずなので、領域も16個あるはずなのです。

改めて図20をよく見ると、A∩B∩C∩Dに相当する領域(AとDの円の内側にあって、BとCの円の外側にある領域)とA∩B∩C∩Dの領域(BとCの円の内側にあって、AとDの円の外側にある領域)が、この図には抜けています。

正しいベン図を図21に示します。

↑ 画像をクリックすると拡大

図21、4つの集合の正しいベン図

このベン図には、4つの閉曲線で区切られた領域に1～16の番号を描き込んであります。図20とは違い、きちんと16個の領域があります。1～16の領域が、何の集合に対応するかを表3に示します。

4つの集合のベン図になると、複雑になって、描き方をしっかり覚えていないと描けなくなっています。さらに5つの集合のベン図になると、図22に示す様に、人が手描きするのが困難なほど複雑な図形なります。

↑ 画像をクリックすると拡大

図22、5つの集合のベン図(Wikipediaから引用)

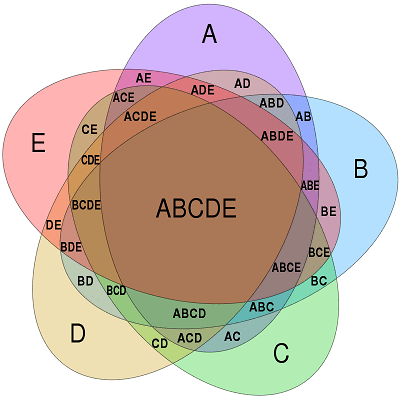
この図は、https://commons.wikimedia.org/wiki/File:Symmetrical_5-set_Venn_diagram.svgから引用しました。この図はCC BY-SA 3.0で公開されています。

以上の様に、4つ以上の集合のベン図は、複雑すぎて、人が描くのが難しかったり、あるいは描けたとしても、直観的に理解できなくなったりしますので、ベン図は3つ以下の集合の場合に使用する事がほとんどです。

次のページでは、論理関数や論理回路の動作の理解のために使われるベン図について説明します。

関連ページ

• Wikipediaのベン図のページ

このサイトの記事が本になりました

書名：Arduino 電子工作

ISBN:978-4-7775-1941-5

→工学社の書籍の内容の紹介ページ

本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。

このサイトの中の人が書いた本です。

書名：電子工作で学ぶ論理回路入門

ISBN:978-4-7775-2280-4

→工学社の書籍の内容の紹介ページ

→この本の紹介記事

本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。