
前のページでは、精度5%の抵抗の値に、E24系列の数値が使われることを説明しました。では、もっと精度の悪い部品の場合、どの様な系列の値が使われるか考えて見ましょう。
最近では精度が10%や20%の抵抗を見かける事はほとんどなくなりました。安価なカーボン抵抗でも5%の精度があります。
一方で、コンデンサなら、5%の精度(Jランク)というのはむしろ良い方で、フィルムコンデンサや容量の小さい(低誘電率系の)セラミックコンデンサでは、10%の精度(Kランク)のものが結構あります。電解コンデンサの場合は20%精度(Mランク)のものが多いようです。容量の大きい(高誘電率系の)セラミックコンデンサでは、+80%,-20%というものもあります。(Zランク) 実例をお見せしましょう。
上の写真は、手元にあったコンデンサの中から3つピックアップしたものを撮影した写真です。
写真左側の茶色いコンデンサは、高誘電率系のセラミックコンデンサです。良く見ると「104Z」と赤い文字で書いてあります。最初の「104」は、容量を表わしています。10×104pF、すなわち0.1μFを意味します。最後の「Z」が精度を表わしています。Zランクのコンデンサの精度は+80%,-20%と、かなり誤差が許容されています。つまり、このコンデンサの容量は、0.08μF~0.18μFの範囲のどこかに入っている事になります。(当然のことながら、これほど精度が悪いコンデンサは、フィルタ回路など、精度の要求される用途には用いられません。電源のパスコンとして使われることがほとんどです)
写真中央の黄色いコンデンサは、フィルムコンデンサです。かなり読みにくいですが、「123K」と黒い文字で書いてあります。最初の「123」は、容量が12×103pF、すなわち0.012μFであることを示しています。最後の「K」は、精度が10%である事を示しています。
写真右側の黄色いコンデンサも、フィルムコンデンサです。「123J」と書いてあります。数字は「123」ですから、中央のコンデンサと同じ0.012μFです。最後の文字「J」は、精度が5%であることを示しています。
Jランク(精度5%)のコンデンサはともかく、Kランク(精度10%)以下のコンデンサの容量をE24系列でラインアップする必要があるでしょうか?前のページで述べたとおり、E24系列の場合、丸め誤差の最大値が5%程度になります。一方で、Kランク以下のコンデンサでは、精度が10%かそれより悪いので、丸め誤差の方が小さくなります。よって、E24系列よりも、公比を大きくして、数字の種類を減らしても、問題がなさそうです。そこで登場するのが、これから説明するE3系列、E6系列、E12系列です。
JIS C 5063では、精度10%の部品にはE12系列を使うこととなっています。E12系列は、初項が1で、公比が1210の等比数列にほぼ近い、2桁の数字の並びです。具体的に書くと、次の様になります。
1.0, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2
公比の1210を計算すると、約1.2115となります。つまり、任意の数値は、それより一つ小さい数値の約21.15%増しということになります。丸め誤差の最大値はその半分ですから、約10.6%ということになります。このように、E12系列を使うと丸め誤差と部品の精度のバランスが、精度10%の部品を使う場合にちょうどよくなるように設定されている事が分かります。
JIS C 5063では、精度20%の部品にはE6系列を使うこととなっています。E6系列は、初項が1で、公比が610の等比数列にほぼ近い、2桁の数字の並びです。具体的に書くと、次の様になります。
1.0, 1.5, 2.2, 3.3, 4.7, 6.8
公比の610を計算すると、約1.4678となります。つまり、任意の数値は、それより一つ小さい数値の約46.78%増しということになります。丸め誤差の最大値はその半分ですから、約23.4%ということになります。このように、E6系列を使うと丸め誤差と部品の精度のバランスが、精度20%の部品を使う場合にちょうどよくなるように設定されている事が分かります。
JIS C 5063では、精度が20%より悪い部品にはE3系列を使うこととなっています。E3系列は、初項が1で、公比が310の等比数列にほぼ近い、2桁の数字の並びです。具体的に書くと、次の様になります。
1.0, 2.2, 4.7
公比の310を計算すると、約2.1544となります。つまり、任意の数値は、それより一つ小さい数値の約115.44%増しということになります。丸め誤差の最大値はその半分ですから、約57.7%ということになります。
E12系列の数値は、E24系列の数値を一つ置きに抜き出したものになっています。同様にE6系列の数値はE12系列の数値を一つ置きに抜き出したものになっています。さらに、E3系列の数値は、E6系列の数値を一つ置きに抜き出したものになっています。この関係を分かりやすい様に表わしたのが次の表です。
| E3系列 | E6系列 | E12系列 | E24系列 |
|---|---|---|---|
| 1.0 | 1.0 | 1.0 | 1.0 |
| 1.1 | |||
| 1.2 | 1.2 | ||
| 1.3 | |||
| 1.5 | 1.5 | 1.5 | |
| 1.6 | |||
| 1.8 | 1.8 | ||
| 2.0 | |||
| 2.2 | 2.2 | 2.2 | 2.2 |
| 2.4 | |||
| 2.7 | 2.7 | ||
| 3.0 | |||
| 3.3 | 3.3 | 3.3 | |
| 3.6 | |||
| 3.9 | 3.9 | ||
| 4.3 | |||
| 4.7 | 4.7 | 4.7 | 4.7 |
| 5.1 | |||
| 5.6 | 5.6 | ||
| 6.2 | |||
| 6.8 | 6.8 | 6.8 | |
| 7.5 | |||
| 8.2 | 8.2 | ||
| 9.1 |
次の表は、ニチコンのUDシリーズという表面実装型アルミニウム電解コンデンサのデータシートより引用したものです。
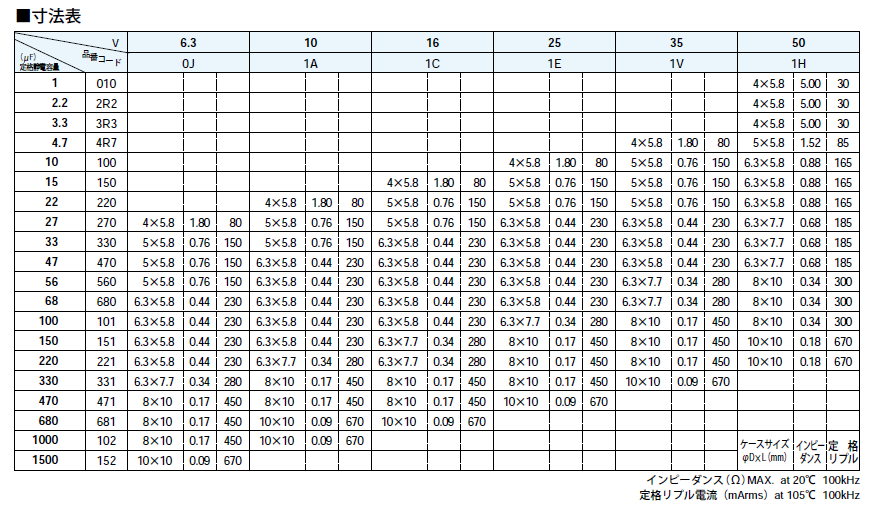 |
このUDシリーズの電解コンデンサの精度は、全て20%(Mランク)です。
表3の一番左の列に容量が書いてあります。10μ~1500μFの間はおおむねE6系列で容量が用意されています。ただし、27μFと56μFは例外的にE12系列の値となっています。
また、1μF~10μFの範囲では、E3系列で容量が用意されています。
このように、精度20%の部品の値はE6系列で用意するというルールは、コンデンサでは、あまり厳密に守られていません。
また次の表は、村田製作所の表面実装型の汎用温度補償用セラミックコンデンサの型番一覧表の一部を引用したものです。
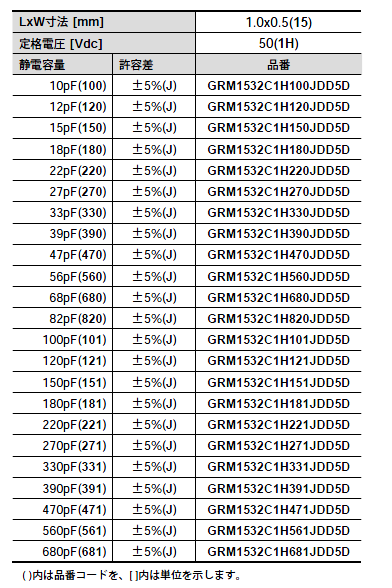 |
この表に載っているコンデンサの精度は全て5%(Jランク)です。本来ならE24系列で容量値がラインナップされているはずです。しかし、表4を見ると、実際にはE12系列で容量値がラインナップされていることが分かります。
これらの例の様に、コンデンサの容量は、必ずしもJIS C 5063の決まりを守っておらず、より少ない種類の容量で済まされている場合が多々あります。よって、コンデンサを使う回路を設計する場合、より数の小さいE系列(E12系列よりもE6系列、E6系列よりもE3系列)に属する容量を優先的に使うように心がけると、より多くの選択肢の中からコンデンサを選ぶことができ、部品調達が楽になります。例えば100μF(E3系列)のコンデンサでも、120μF(E12系列)のコンデンサでも動くような回路の場合、100μFを使うようにしましょう。
次に、LMC555というタイマICを用いたCR発振回路について考えます。
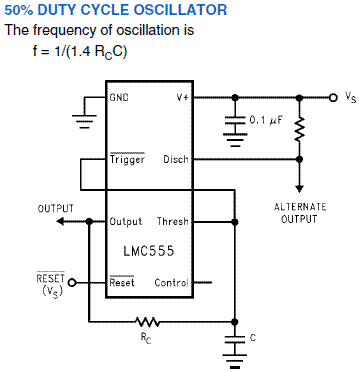
この回路図は、LMC555のデータシートから引用した、デューティー比50%の方形波が発振できるCR発振回路の回路図です。この回路の発振周波数fは抵抗値RCとコンデンサの容量Cにより、f=11.4RCCという式から求まります。ここで、fはRCとCの積で決まることに注意してください。
CR直列回路あるいはCR並列回路において、抵抗値と容量の積の事を時定数と呼びますが、抵抗値と容量の個々の値ではなく、それらの積(すなわち時定数)が回路の動作を決めることがしばしばあります。
目的の時定数を得るための抵抗値と容量の組み合わせを得るためには、容量を先に決めて、抵抗値は目標の時定数を容量で割った商から求める方が、抵抗値を先に決めるよりもうまくいきます。これは、E24系列の抵抗値が確実に手に入るのに対して、コンデンサの方は、E6系列やE12系列など、より少ない選択肢から容量を選択しなければならないという事情が原因になっています。
具体的な例を挙げて説明しましょう。図7の回路が12.345kHzの発振をするようにのRCとCを決定する問題を解いてみましょう。ただし、抵抗RCはE24系列から値を選べるものとし、コンデンサCはE6系列から値を選ばないといけないとします。
時定数RCCはRCC=11.4fという式より、1÷{1.4×(12.345×103)}=5.7860×10-5[s]と求まります。(時定数の単位はs、つまり秒です)
ここで先にRCを10kΩ(これはE24系列の値)に決めたとします。そうするとC=(5.7860×10-5)÷(10×103)=5.7860×10-9[F]=5786.0[pF]と求まります。ところがCの値はE6系列の数値の中から選ばなければなりませんので、E6系列の中で一番近い4700pFを選ぶことになります。この場合の回路の発振周波数は1÷{1.4×(10×103)×(4700×10-12)}=15.198×103[Hz]=15.198[kHz]となり、目標の12.345kHzよりも23.1%も高い周波数になってしまいます。
一方でCの値を4700pF(これはE6系列の値)に先に決めた場合だと、RC=(5.7860×10-5)÷(4700×10-12)=12.311×103[Ω]=12.311[kΩ]と、RCが求まります。RCをE24系列中で最も近い12kΩに丸めるとすると、発振周波数は1÷{1.4×(12×103)×(4700×10-12)}=12.655×103[Hz]=12.665[kHz]となります。これは目標の12.345kHzより2.6%高い周波数となり、RCを先に決めた場合の丸め誤差である23.1%よりも、かなり小さな丸め誤差で済んでいることが分かります。
今回は5%よりも精度の悪い部品(特にコンデンサ)で使われるE3系列、E6系列、およびE12系列について書きました。次のページでは5%よりも精度の良い部品について書きます。
