

E3系列・E6系列・E12系列・E24系列の数表を見たい方は、表2をご覧ください。
E48系列・E96系列・E192系列の数表を見たい方は、表5をご覧ください。
電子部品屋さんに行って、抵抗の置いてある部品棚を見てください。1kΩの次に大きい抵抗は何kΩですか?1.1kΩですね。その後、1.2kΩ、1.3kΩ、1.5kΩ、1.6kΩ、1.8kΩ、2kΩ、2.2kΩ、2.4kΩ、2.7kΩ・・・と続きます。「どうしてこんなに中途半端な値を使うんだろう?」とか、「1kΩ、2kΩ、3kΩ、4kΩ・・・としてくれれば分かりやすいのに」と思った事はありませんか?今回はそういう疑問に答えます。
仮に1kΩ、2kΩ、3kΩ、4kΩ・・・と、1kΩずつ増える数字の並びになっていると仮定してください。8kΩの後は9kΩ,10kΩ,11kΩ・・・と続いていきます。この場合、良く考えると、1~1MΩ(1000kΩ)の範囲に1000種類もの抵抗値があることになります。これは明らかに多すぎです。部品棚に収まりません。
そこで、10kΩに達したら10kΩずつ増える事にし、さらに100kΩに達したら、100kΩずつ増える事を考えます。分かりやすい様に1kΩから順に書くと、1kΩ、2kΩ、(中略)、8kΩ、9kΩ、10kΩ、20kΩ、(中略)、80kΩ、90kΩ、100kΩ、200kΩ、(中略)、800kΩ、900kΩ、1MΩという抵抗値の並びになります。これなら1kΩから1MΩまでを28種類の抵抗値で網羅できます。
ここで、その抵抗値の並び方をグラフで確認してみます。
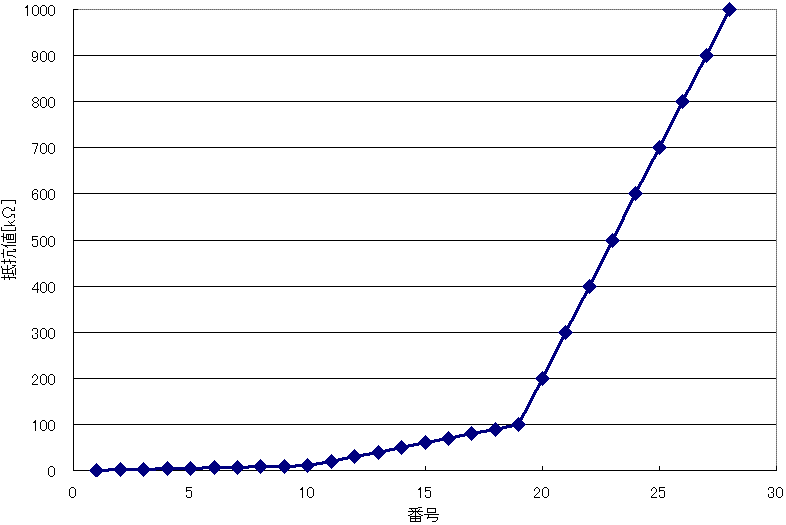
そうすると、グラフが傾きの異なる3本の直線でできていることが分かります。傾きの変わる点は10kΩ(10番目)と100kΩ(19番目)の2点です。これら2点の前後において、何が起こっているのか考えてみましょう。
10kΩまでは、抵抗値が1kΩずつ増えていました。10kΩからは、抵抗値が10倍の10kΩずつ増えていきます。同様に100kΩまでは抵抗値が10kΩずつ増えますが、100kΩからは抵抗値が10倍の100kΩずつ増えていきます。これが傾きが不連続になる原因です。
その結果、次の様な不都合が起こります。9kΩの次は10kΩですが、これは9kΩの約11.1%増しです。10kΩの次は20kΩですが、これは10kΩの100%増しです。一つ前の抵抗値からの増加率が、こんなにも劇的に変化してしまいます。これでは、抵抗値の微調整の時などに、不都合が生じます。
例えば、あなたが今、10kΩの抵抗を使った回路の特性を測っていると想像してみてください。そして測定をした結果、10kΩの抵抗を微調整すれば、より理想的な特性が得られる事が分かったとします。10kΩを下げる方向には簡単に微調整できます(9kΩに交換すれば抵抗値を10%下げられる)が、10kΩを上げる方向には微調整できません(20kΩに交換すれば、抵抗値が倍になってしまう)。これでは不便ですね。
参考までに、図1を、抵抗値を対数目盛にして書き直したのが、次のグラフです。山の3つある曲線になっていますね。対数目盛は増加した値ではなく、増加の比率を観察する目盛の取り方です。このグラフを見ると、抵抗値が一定比率で上昇していないのがよく分かります。
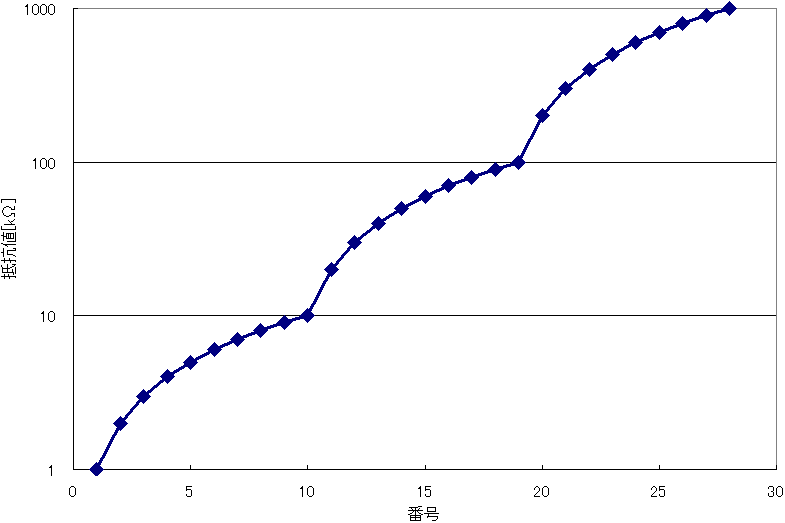
抵抗値を全てキリのいい値にするには、抵抗値を一定値ごと増加する必要がありました。つまり、抵抗値の並びは、等差数列になっていたのです。これを等比数列にすれば、図1の様にグラフの傾きが不連続になることもなく、よって10kΩ付近で抵抗値が微調整できなくなる様な不具合もなくなります。
等比数列とは、隣り合う数の比が一定になるような数の並びのことです。例えば、次の様な抵抗値の並びは、等比数列になっています。
1kΩ、2kΩ、4kΩ、8kΩ、16kΩ、32kΩ、64kΩ、128kΩ・・・
この数字の並びを見ていると、数字が2倍ずつになっています。これで等比数列の抵抗値の並びができたのですが、このままでは使い勝手が良くありません。理由は2つあります。
まず、倍倍ゲームで数字が増えてしまうと、抵抗値の微調整ができません。隣り合う数の比は、2ではなく、1.1とか1.05など、もっと小さな数である必要がありそうです。
また、2を何回かけてもぴったり10になりません。8kΩの次は、10kΩを通り越して16kΩになってしまいます。そのため、先ほどの数列の中の2桁の抵抗値(16kΩ、32kΩ、64kΩ)を10で割った値(1.6kΩ、3.2kΩ、6.4kΩ)は、先ほどの数列の中にはないという不都合が生じます。この問題は隣り合う数の比(これを公比と呼ぶ)をN10(Nは任意の整数)にすれば解決します。N10は、N回かけると10になる数(10のN乗根)を表わします。
そこで、公比を、例えば2410にしてみます。2410を関数電卓で計算すると、1.100694171…となります。試しにこの数を24乗すればぴったり10になります。この場合、抵抗値の並びは次の様になります。(四捨五入して、小数点以下3桁まで表示)
1.000kΩ、1.101kΩ、1.212kΩ、1.334kΩ、1.468kΩ、1.616kΩ、1.778kΩ、1.957kΩ、2.154kΩ、2.371kΩ、2.610kΩ、2.873kΩ、3.162kΩ、3.481kΩ、3.831kΩ、4.217kΩ、4.642kΩ、5.109kΩ、5.623kΩ、6.190kΩ、6.813kΩ、7.499kΩ、8.254kΩ、9.085kΩ、10.000kΩ、11.007kΩ、12.115kΩ、(中略)、908.518kΩ、1000.000kΩ
当然この数列には、10kΩも含まれています。これをグラフ化したものが次のグラフです。
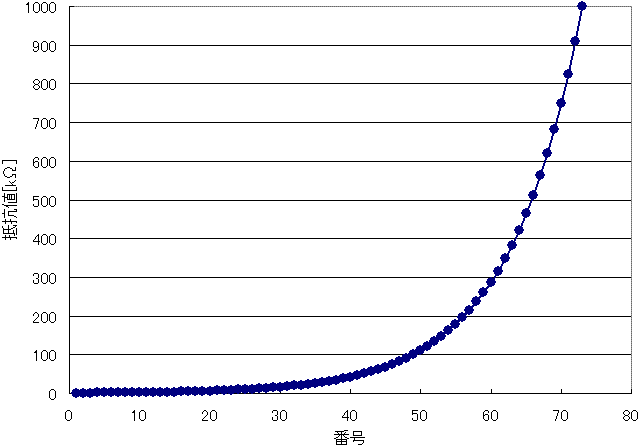
全体として滑らかな曲線になっていることが分かります。図1の様な、傾きの不連続点がありません。
さらに図3の縦軸を対数目盛にすると、次のグラフになります。一定の比率で抵抗値が上昇していることが分かりますね。
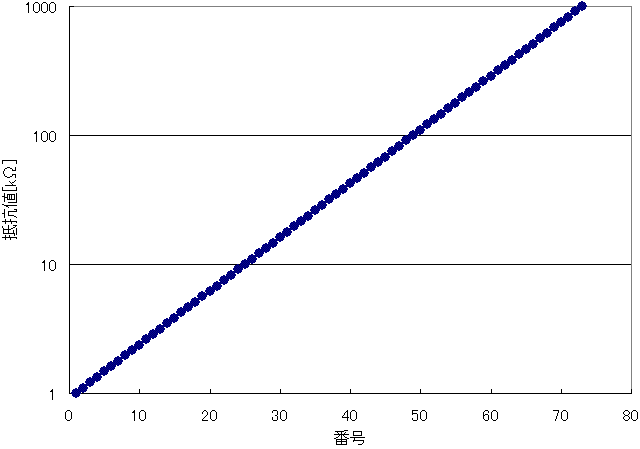
加えて言うと、約1.1(2410)の公比は、精度が5%の抵抗の抵抗値として使うのに、ちょうど都合がいいのです。
例えば公比が1.01のように小さい値だと、1kΩから10kΩまでに、数字が232個くらい並びます。抵抗値の種類が多すぎる上に、公比が抵抗の精度に見合っていないくらい小さな値になっています。5%の精度なら、公称値(メーカーが表示している値)の0.95倍~1.05倍の範囲で抵抗値がばらつきます。それほど多くばらつくのに、1%刻みで公称値を用意しても意味がありません。
逆に公比が1.5849(510)のように大きいと、1kΩから10kΩまでの間に、公称値が6個あることになります。抵抗値の種類が少ないので、用意しなければならない在庫の種類が減るというメリットはありますが、1kΩの次が1.5849kΩと60%近く大きな値になるので、5%の高い精度を十分活かせなくなります。例えば1.2kΩの抵抗を使うのが理想的な場合を考えると、1kΩと1.5849kΩの内、1.2kΩにより近い1kΩを選択することになります。この抵抗値の丸めにより、16.7%の丸め誤差が発生します。つまり、抵抗の精度よりも、丸め誤差の方がかなり大きくなってしまうわけです。
公比が約1.1だと、抵抗値が一つ前の抵抗値の10%増しになります。よって、丸め誤差の最大値は、その半分の5%になります。つまり、ちょうど精度と丸め誤差がバランスしている状態です。
抵抗値を公比が2410(≒1.100694171)の等比数列にすれば、等差数列の時の様な不具合は解決し、しかも5%精度の抵抗の場合、精度と丸め誤差のバランスがいい事が分かりました。一方で無限に桁が続く小数になってしまうので、実用上の問題がが発生します。
そこで、公比が2410の等比数列にほぼ等しい値の2桁の数字を使えばいいという考え方が出ました。その結果できたのが、E24系列という数列です。具体的にはE24系列は次の数列です。抵抗値の場合で考えるなら、この数列の各数字の後ろにkΩやΩの単位を加えて考えてください。
1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.7, 3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8, 7.5, 8.2, 9.1
Wikipediaの記事によると、E24系列はJIS C 5063で規格化されているようです。抵抗やコンデンサの値に広く使われています。
E24系列の数列は、初項(数列の最初の数字)が1で公比が2410の等比数列とほぼ同じ値ですが、単純にその等比数列を小数点以下2桁で四捨五入した値とは一致しません。分かり易いように、次の表でE24系列と等比数列を比較してみましょう。
| 番号 | E24系列 | 等比数列 (小数点以下3桁まで) |
|---|---|---|
| 1 | 1.0 | 1.000 |
| 2 | 1.1 | 1.101 |
| 3 | 1.2 | 1.212 |
| 4 | 1.3 | 1.334 |
| 5 | 1.5 | 1.468 |
| 6 | 1.6 | 1.616 |
| 7 | 1.8 | 1.778 |
| 8 | 2.0 | 1.957 |
| 9 | 2.2 | 2.154 |
| 10 | 2.4 | 2.371 |
| 11 | 2.7 | 2.610 |
| 12 | 3.0 | 2.873 |
| 13 | 3.3 | 3.162 |
| 14 | 3.6 | 3.481 |
| 15 | 3.9 | 3.831 |
| 16 | 4.3 | 4.217 |
| 17 | 4.7 | 4.642 |
| 18 | 5.1 | 5.109 |
| 19 | 5.6 | 5.623 |
| 20 | 6.2 | 6.190 |
| 21 | 6.8 | 6.813 |
| 22 | 7.5 | 7.499 |
| 23 | 8.2 | 8.254 |
| 24 | 9.1 | 9.085 |
この表で赤字で書いた数字が、等比数列の値を小数点以下2桁で四捨五入した値と一致していません。どういう事情でこうなったのかは知りませんが、四捨五入で求めた値より、表の赤字で書いた値を使う方が、実用上便利だからという説もあります。
E24系列の1kΩ~1MΩの抵抗値を、グラフ化したのが次の2つのグラフです。
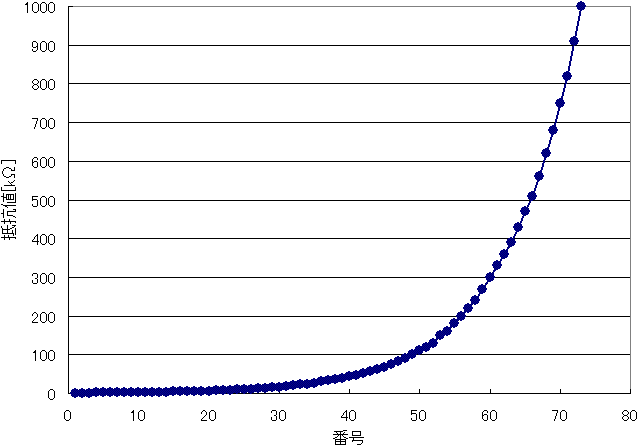
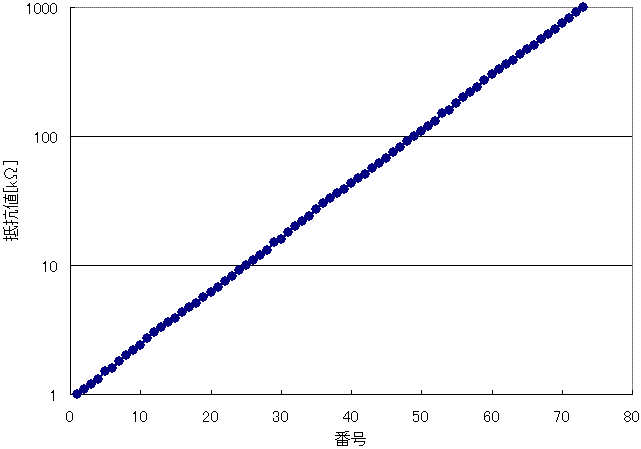
図5と図6はそれぞれ図3と図4とほぼ同じグラフになっているのが分かります。
抵抗値やコンデンサの容量などのラインアップは、等差数列で揃えるよりも、等比数列でそろえる方が良いことを説明しました。しかしながら、等比数列だと、非常にキリの悪い数字になるので、2桁に丸めたE24系列が用いられることも説明しました。
E24系列は、5%精度の抵抗やコンデンサには向いている数列ですが、もっと精度が悪いか、もっと精度が良い抵抗・コンデンサには、E24系列以外の数列が向いているはずです。
次のページでは、5%よりも精度の悪い部品において使われるE系列(E3系列、E6系列、E12系列)について説明します。
