| 2015年06月13日 | 公開。 |
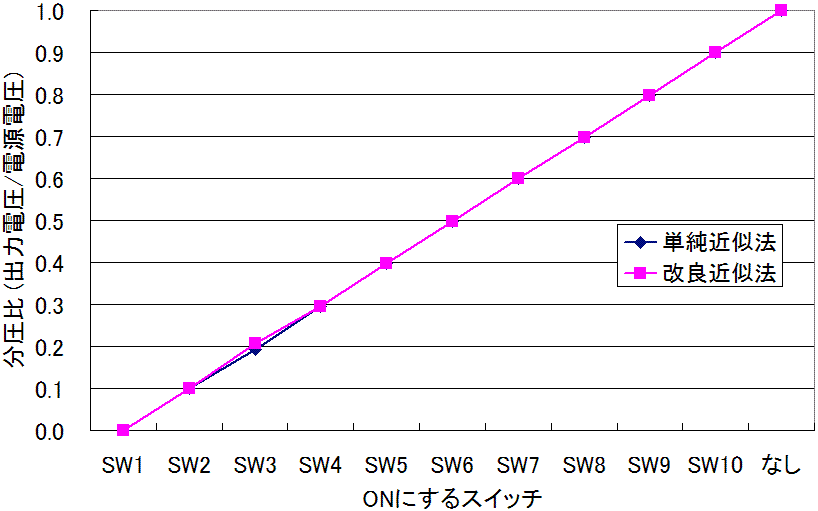
前のページでは、ノイズマージン(ノイズ電圧の許容値)が最大になる様に、出力電圧を均等に配分する設計法を解説しました。この方法は、言い換えれば、ONにするスイッチの番号と、分圧比の関係が、前のページに載せた図12の様に、ほぼ直線になるように設計する方法だといえます。ページを繰らなくていいように、図12をここに再掲します。

この様な直線関係のグラフが得られる設計法は、抵抗値の誤差が無視できるくら小さい場合は、確かにうまく動作します。しかしながら、抵抗値には許容誤差が設けられています。安価なカーボン抵抗を使う場合、許容誤差は普通5%と、比較的大きな値に設定されています。
結論からいうと、5%という大きな誤差の抵抗を使うと、図12の様に、直線関係のグラフになる様に設計する方法は、最適な設計法とはいえないのです。この設計法は、ノイズに対するマージンは大きく取れますが、抵抗値の誤差に対しては敏感な設計法なのです。
ここで、図12の改良近似法のグラフが得られる分圧回路の回路図を振り返ってみます。
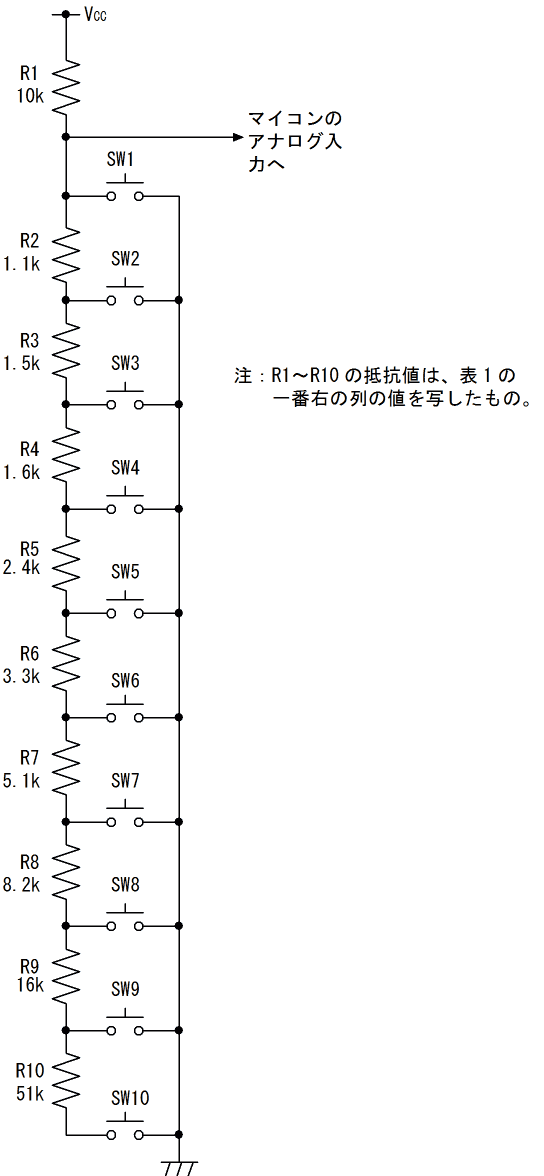
図13の回路で、それぞれの抵抗に±5%の範囲で誤差が生じる時、分圧比がどの範囲でばらつくかを考えて見ます。
まずSW1をONにした場合について考えます。この場合は等価回路が図15の様になり、抵抗値の誤差に関係なく、分圧比が0になる事が分かります。
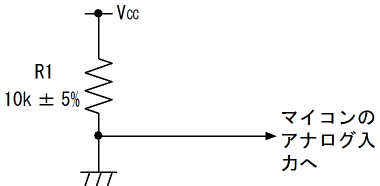
次にSW2をONにした場合について考えます。この場合、等価回路は図15の様になり、R1とR2の分圧回路となる事が分かります。
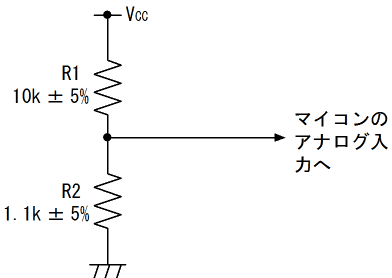
R1とR2は、それぞれ独立して抵抗値に誤差を持ちますが、分圧比が最小になるのは、R1が5%だけ公称値の10kΩより大きくなり(10.5kΩ)、R2が5%だけ公称値の1.1kΩより小さくなる(1.045kΩ)場合です。この時の分圧比を計算すると、1.045÷(1.045+10.5)≒0.09052となります。
一方で、分圧比が最大になるのは、R1が5%だけ公称値より小さくなり(9.5kΩ)、R2が5%だけ公称値より大きくなる(1.155kΩ)場合です。この時の分圧比を計算すると、1.155÷(1.155+9.5)≒0.10840となります。
表2に示したように、抵抗値に誤差がなければ分圧比は0.09910になるのですが、抵抗値の誤差を考慮すると、分圧比は0.09052~0.10840の範囲でばらつく事になります。
次にSW3をONにした場合について考えます。この場合の等価回路は図16の様になり、R1とR2+R3の分圧回路となる事が分かります。
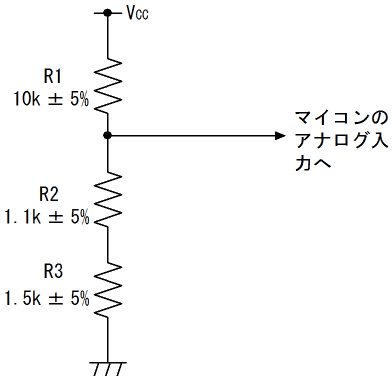
図16の回路で分圧比が最小になるのは、R1が公称値より5%大きく、R2とR3がいずれも公称値より5%小さい場合です。この場合の分圧比を計算すると、0.19044となります。
また分圧比が最大になるのは、R1が公称値より5%小さく、R2とR3がいずれも公称値よりも5%大きい場合です。この場合の分圧比は0.22322となります。
同様の方法で、全ての場合について、抵抗値の誤差の影響で分圧比がどの範囲でばらつくかを計算した結果が表3と図17になります。
| ONにする スイッチ |
分圧比の 最小値 |
分圧比の 最大値 |
ノイズマージン (×VCC) |
|---|---|---|---|
| SW1 | 0.00000 | 0.00000 | |
| 0.09052 | |||
| SW2 | 0.09052 | 0.10840 | |
| 0.08204 | |||
| SW3 | 0.19044 | 0.22322 | |
| 0.05214 | |||
| SW4 | 0.27536 | 0.31704 | |
| 0.05684 | |||
| SW5 | 0.37388 | 0.42179 | |
| 0.05070 | |||
| SW6 | 0.47249 | 0.52249 | |
| 0.05326 | |||
| SW7 | 0.57576 | 0.62376 | |
| 0.05356 | |||
| SW8 | 0.67732 | 0.71943 | |
| 0.06063 | |||
| SW9 | 0.78006 | 0.81248 | |
| 0.07837 | |||
| SW10 | 0.89084 | 0.90884 | |
| 0.09116 | |||
| なし | 1.00000 | 1.00000 | |
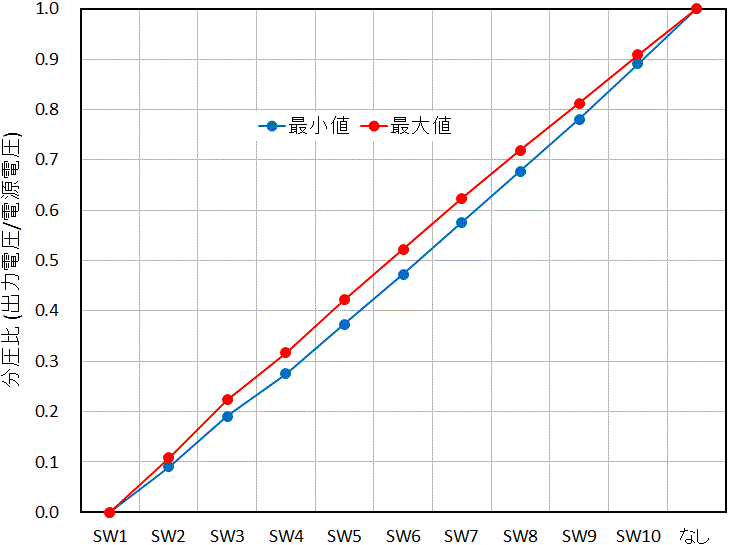
図17を見ると、グラフの右端や左端では、分圧比は抵抗の誤差の影響をあまり受けていない事が分かります。一方で、グラフの中央部では、分圧比は抵抗の誤差の影響を大きく受ける様子が見て取れます。
また表3には、一番右の列にノイズマージンを計算して計算しておきました。
例えば、この表のノイズマージンの列の上から2番目の数字は、0.08204となっています。これは、SW3をONにした場合の分圧比の最小値(0.19044)から、SW1をONにした場合の分圧比の最大値(0.10840)を引いて求めた値です。
これは、SW2をONにした場合に、0.08204VCC(仮にVCCが5Vとすると、0.4102V)までの振幅のノイズなら、加わってもSW3をONにしたと誤判定しない事を示しています。また同時に、SW3をONにした場合に、0.08204VCCまでの振幅のノイズなら、加わってもSW2をONにしたと誤判定しない事を示しています。
仮に抵抗値に誤差がないとすれば、図13の回路は、どのスイッチをONにしたとしても約0.1VCCのノイズマージンが確保できる回路なのですが、抵抗値に5%の誤差がある場合は、SW5~7あたりをONにした場合に分圧比が抵抗の誤差の影響を大きく受け、SW5とSW6の間のノイズマージンは0.0570VCCと、抵抗に誤差がない場合の半分程度まで悪化している(すなわち、ノイズの影響を受けやすくなっている)事が分かります。
出力電圧を均等に配分する回路を精度の低い抵抗で構成すると、この様な問題発生するため、ノイズマージンの最悪値を改善するには、別の設計手法を使う必要が出てきます。
次のページでは、抵抗値の誤差が、抵抗分圧型のキーパッドの分圧比にどの様な影響を与えるかについて、数式を用いて、さらに詳しく説明しています。
 |
商品名 | I/Oピン一つで読める4X4キーパッドキット |
| 税抜き小売価格 | 900円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッドキットサポートページ |
 |
商品名 | I/Oピン一つで読める4X4キーパッド(完成品) |
| 税抜き小売価格 | 1380円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッド(完成品)サポートページ |
 |
商品名 | I/Oピン一つで読める4X5キーパッドキット |
| 税抜き小売価格 | 2400円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X5キーパッドキットサポートページ |
