前のページでは、10個のスイッチをセンシングするための抵抗分圧器の設計例を紹介しました。この回路の設計法を説明します。
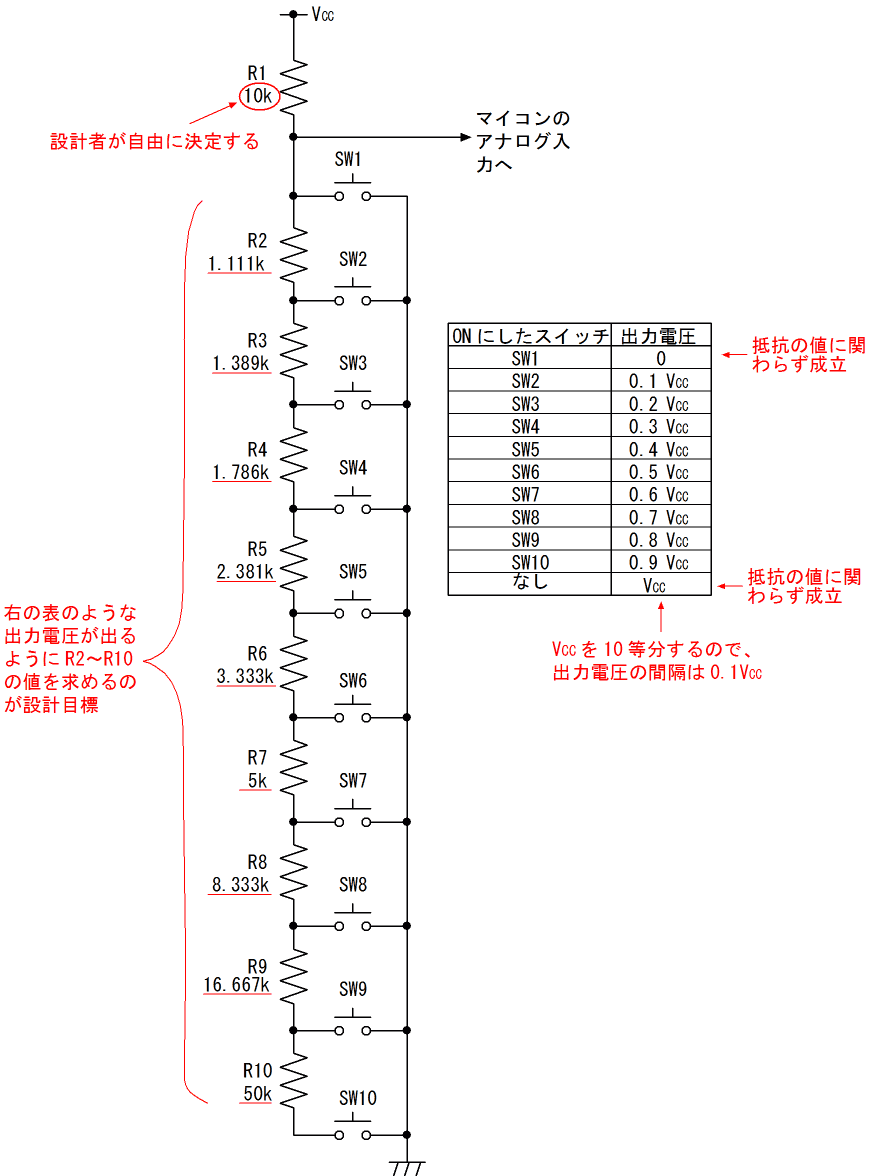
まず、図4の回路図を一部加筆して再掲します。

抵抗が10個、スイッチが10個ある回路ですが、出力電圧が均等になるように、抵抗値を決めるのが設計の目標です。すなわち、表にあるように、SW1をONにした時の出力電圧が0、SW2をONにした時の出力電圧が0.1VCC、・・・、SW10をONにした時の出力電圧が0.9VCC、全てのスイッチをOFFにした時の出力電圧がVCCとなるように、R2~R10の値を定めるのが設計目標です。ただし、R1の値は設計者が自由に決定する事ができます。ここではR1が10kΩの場合について説明する事にします。
まず、全てのスイッチがOFFの場合を考えましょう。この場合は、次の図のように、出力をR1でVCCにプルアップした回路と等価となります。よって、R2~R10 の値が何であれ、出力電圧はVCCとなります。
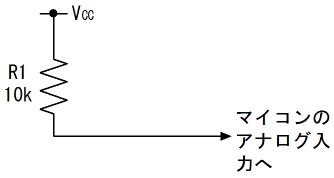
次にSW1のみがONの場合について考えます。この場合の等価回路は次の図のようになり、出力端子がGNDとショートしていますから、R2~R10の値に関わらず、出力電圧は0となります。
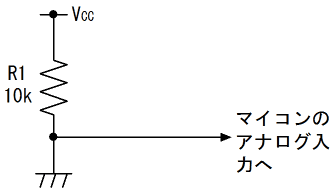
次にSW2のみがONの場合について考えます。この場合の等価回路は、次の図のように、R1とR2の2つの抵抗からなる分圧回路となります。
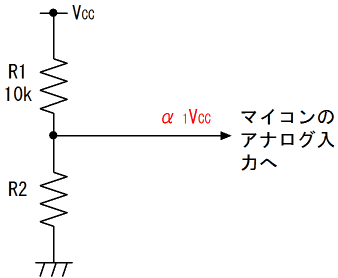
R1の抵抗値をR1(=10[kΩ])、R2の抵抗値をR2とすると、分圧比(出力電圧と電源電圧VCCの比)α1は次の様に求まります。(以下同様にR3の抵抗値をR3、R4の抵抗値をR4・・・とする)
この式をR2について解くと、次の様になります。
ここでR1=10[kΩ]、α1=0.1を代入して計算すると、R2≒1.111[kΩ]となります。
次にSW3のみがONの場合を考えます。この場合の等価回路は、次の図のような分圧回路となります。
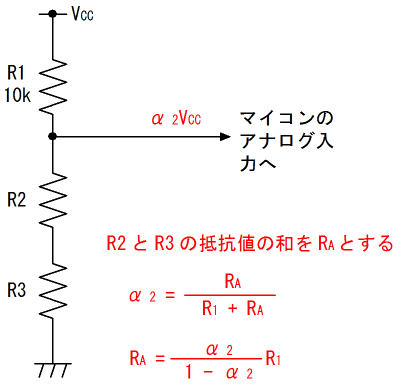
ここで、R2とR3の抵抗値の和(直列合成抵抗)をRA、分圧比をα2とすると、(2)を求めた際と同様に、RAは次の様に求まります。
この式にR1=10[kΩ]、α2=0.2を代入して計算すると、RA=2.5[kΩ]と求まります。さらにこの値からR2(1.111kΩ)を引くと、R3≒1.389[kΩ]となります。
次にSW4のみがONの場合を考えます。この場合の等価回路は次の図のようになります。
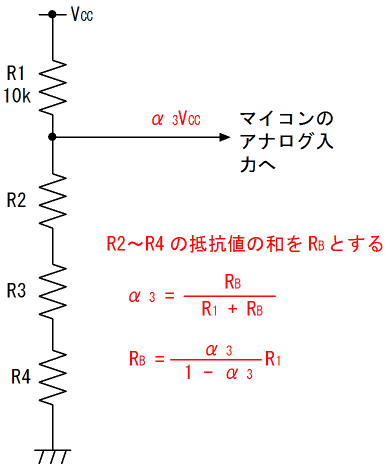
R2~R4の抵抗値の和をRBとすると、図10の場合と同様の計算でR1=10[kΩ]、α3=0.3としてRB≒4.286[kΩ]と求まります。ここからRA(2.5kΩ)を引くとR4≒1.786[kΩ]と求まります。以下、R5~R10の抵抗値も同様の方法で求まります。
実際には抵抗値をE24系列の中の値から選ぶ必要があります。そのために、R2~R10の値を、それぞれ最も近いE24系列の値に丸めてもいいのですが、もう少し精度の良い丸め方があります。
図9を参照して、R2をE24系列の値で近似する事を考えます。理論的にはR2≒1.111[kΩ]ですが、この値はE24系列にはないので、最も近い1.1kΩを選ぶことにします。E24系列の値で近似したR2の値をR2'と表わす事にすると、R2'=1.1[kΩ]ということになります。
次に図10を参照して、R3をE24系列の値で近似する事を考えます。RA=2.5[kΩ]ですから、ここからR2'(1.1kΩ)を引くと1.4kΩとなります。R3の理論的な値(1.389kΩ)ではなく、RA−R2'(1.4kΩ)をE24系列の値で近似するところがポイントで、こうする事によって、抵抗値の近似誤差が蓄積しないように計算する事ができます。
α2の誤差を小さくしたければ、当然RAの誤差を小さくしなければなりません。RA=R2+R3ですので、R2とR3を独立してE24系列の値に丸めると、丸め誤差の影響を2重に受けてしまいます。一方で、RA−R2'の値をE24系列の値に丸めれば、RAは丸め誤差の影響を2重に受ける事を避けられます。(R2'はE24系列に丸めた後の値であることに注意)
1.4kΩをE24系列の値で近似するとすれば、1.3kΩと1.5kΩが候補になります。どちらを選んでも1.4kΩとの差は0.1kΩです。しかし、1.4kΩは1.3kΩの7.7%増しで、1.5kΩは1.4kΩの7.1%増しだという具合に、比で考えれば、1.5kΩの方が1.3kΩよりも良い近似ということになります。よって、R3のE24系列の近似値R3'は、1.5kΩとなります。
一方で、単純にR3の理論値(1.389kΩ)をE24系列の値で近似すると1.3kΩとなりますので、R3'(1.5kΩ)は単純な近似法の値と異なっていることが分かります。
R4のE24系列上の近似値であるR4'を求める場合は、RB(4.286kΩ)からR2'(1.1kΩ)とR3'(1.5kΩ)を引いた値を計算し(4.286−1.1−1.5=1.686kΩ)、その値をE24系列に丸めて1.6kΩとすればいいです。この場合も、単純にR4の理論値(1.786kΩ)をE24系列に丸めた値の1.8kΩとは異なる選択になっています。
R2~R10の理論値を単純にE24系列の値に丸める方法を単純近似法と呼び、抵抗値の近似誤差が蓄積しない丸め方を改良近似法と呼ぶことにします。図6の回路のR2~R10を2つの近似法でE24系列の値に近似した結果を次の表にまとめました。赤字で書いてある部分が、2つの近似法で異なる部分です。
| 抵抗 | 理論値[kΩ] | 単純近似法に よる近似値 [kΩ] |
改良近似法に よる近似値 [kΩ] |
|---|---|---|---|
| R2 | 1.111 | 1.1 | 1.1 |
| R3 | 1.389 | 1.3 | 1.5 |
| R4 | 1.786 | 1.8 | 1.6 |
| R5 | 2.381 | 2.4 | 2.4 |
| R6 | 3.333 | 3.3 | 3.3 |
| R7 | 5.000 | 5.1 | 5.1 |
| R8 | 8.333 | 8.2 | 8.2 |
| R9 | 16.667 | 16 | 16 |
| R10 | 50.000 | 51 | 51 |
それでは、2つの近似法で、分圧回路の分圧比の誤差が、どのように異なるか調べてみます。分圧比の計算結果を次の表にまとめました。赤字で書いてある部分が、2つの近似法で異なる部分です。
| ONにするスイッチ | 分圧比の理論値 | 単純近似法の 場合の分圧比 (カッコ内は誤差) |
改良近似法の 場合の分圧比 (カッコ内は誤差) |
|---|---|---|---|
| SW1 | 0.00000 | 0.00000 (0.00000) |
0.00000 (0.00000) |
| SW2 | 0.10000 | 0.09910 (−0.0090) |
0.09910 (−0.0090) |
| SW3 | 0.20000 | 0.19355 (−0.00645) |
0.20635 (+0.00635) |
| SW4 | 0.30000 | 0.29577 (−0.00423) |
0.29577 (−0.00423) |
| SW5 | 0.40000 | 0.39759 (−0.00241) |
0.39759 (−0.00241) |
| SW6 | 0.50000 | 0.49749 (−0.00251) |
0.49749 (−0.00251) |
| SW7 | 0.60000 | 0.60000 (0.00000) |
0.60000 (0.00000) |
| SW8 | 0.70000 | 0.69880 (−0.00120) |
0.69880 (−0.00120) |
| SW9 | 0.80000 | 0.79675 (−0.00325) |
0.79675 (−0.00325) |
| SW10 | 0.90000 | 0.90020 (+0.00020) |
0.90020 (+0.00020) |
| なし | 1.00000 | 1.00000 (0.00000) |
1.00000 (0.00000) |
SW3をONにする場合に注目すると、単純近似法の場合、分圧比に−0.00645の誤差が生じているのに対し、改良近似法の場合、誤差が+0.00635とわずかに小さくなっています。
表2の数値を元に、ONにするスイッチと分圧比の関係をグラフ化したのが次のグラフです。
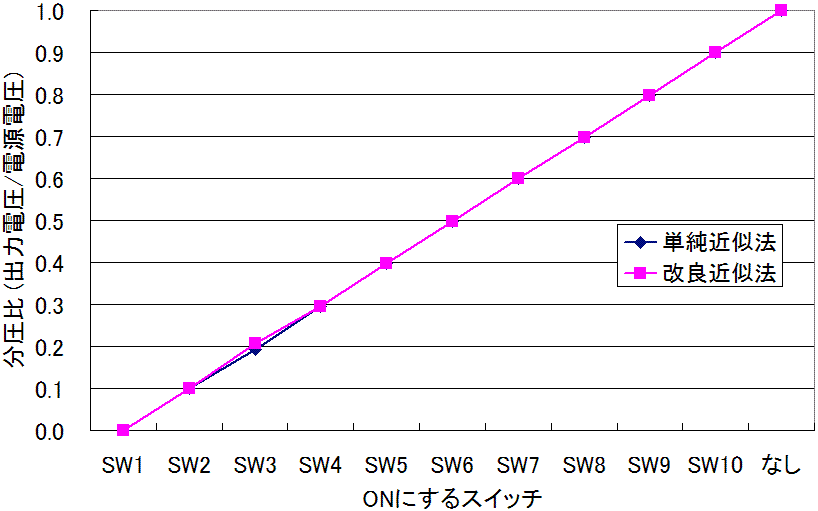
いずれの近似法を使っても、ONにするスイッチと出力電圧(分圧比×電源電圧)の関係が、ほぼ直線になっているのが分かります。数値上は改良近似法の方が、単純近似法よりも直線関係に近くなるのですが、グラフで比較して判断できるほどの差ではありません。
今回は、出力電圧を均等に配分するための抵抗値の決め方と、抵抗値をE24系列で近似する方法について説明しました。次のページでは、抵抗の精度(許容誤差)がどのように出力電圧に影響するかを説明します。
 |
商品名 | I/Oピン一つで読める4X4キーパッドキット |
| 税抜き小売価格 | 900円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッドキットサポートページ |
 |
商品名 | I/Oピン一つで読める4X4キーパッド(完成品) |
| 税抜き小売価格 | 1380円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッド(完成品)サポートページ |
 |
商品名 | I/Oピン一つで読める4X5キーパッドキット |
| 税抜き小売価格 | 2400円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X5キーパッドキットサポートページ |
