↑ 画像をクリックすると拡大
図18、2本の抵抗で構成された分圧回路
| 2023年06月05日 | 公開。 |
前のページの図17に示した様に、この記事で紹介している抵抗分圧式のキーパッドは、分圧比が0.5に近くなると(出力電圧が0.5VCCに近くなると)、抵抗値の誤差の影響で、出力電圧が設計値から外れやすくなります。逆に、分圧比が0付近または1付近(出力電圧が0付近またはVCC付近)の場合は、分圧比(または出力電圧)が抵抗値の誤差の影響をあまり受けません。
この現象は、抵抗分圧式のキーパッドだけではなく、抵抗を使った分圧回路全般で発生する現象です。この章では、分圧回路を構成する抵抗の値の誤差が、分圧比にどの様な影響を与えるかについて考えてみます。
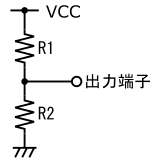
図18に示す様な、2本の抵抗、R1とR2からなる分圧回路について考えます。この回路において、電源電圧はVCC[V]、R1の公称値はR1[Ω]、R2の公称値はR2[Ω]とします。
参考:公称値とは、メーカーが表示している素子値の事です。
2本の抵抗R1とR2の抵抗値に誤差がなく、公称値通りの抵抗値(R1およびR2)だったとすると、この分圧回路の出力電圧Vtypと分圧比αtypは、それぞれ式(4)と式(5)で表わされます。
参考:Vtypやαtypのtypは、typical value(典型値)の略です。典型値とは、数値に分布がある場合に、その数値を表わす典型的な数値を指し、代表値とも呼ばれます。典型値には、平均値、中央値、最頻値などが用いられる事が多いです。ここでは、出力電圧の典型値Vtypと分圧比の典型値αtypは、抵抗値に誤差がなかった場合の、それぞれ出力電圧と分圧比という意味で使っています。言い換えれば、Vtypとαtypは、それぞれ、設計上の出力電圧と、設計上の分圧比という事になります。
次に、抵抗値が公称値から誤差を持つ場合について考えます。抵抗値R1とR2が、公称値からεの許容誤差を持っているとして、その許容誤差が分圧比に与える影響を考えましょう。
ここでεは、抵抗値が持つ誤差の、公称値に対する比率を表します。またεは百分率ではなく、例えば許容誤差が5%ならε=0.05、許容誤差が10%ならε=0.1とします。つまり、公称値R1の抵抗の実際の抵抗値は、(1-ε)R1～(1+ε)R1の範囲にあるとします。
また、2つの抵抗の許容誤差は同じとします。例えば、R1には許容誤差5%の抵抗を使い、R2には許容誤差1%の抵抗を使うといった事は想定しません。
R1の抵抗値が許容誤差の範囲内で最大の値を取り、R2の抵抗値が許容誤差の範囲内で最小の値を取る時に、分圧比は最小の値を取ります。この最小の分圧比をαminとすると、αminは次の式で与えられます。
また、R1の抵抗値が許容誤差の範囲内で最小の値を取り、R2の抵抗値が今日誤差の範囲内で最大の値を取る時に、分圧比は最大の値を取ります。この最大の分圧比をαmaxとすると、αmaxは次の式で与えられます。
分圧回路の設計上の分圧比はαtypですが、実際には、分圧回路をたくさん作ると、分圧比がαminからαmaxの範囲で分布する事になります。
式(6)や式(7)では、αminやαmaxはR1、R2およびεの関数として表現されていますが、εとαtypの関数としても表現する事ができます。
式(5)を変形すると、次の式が得られます。
式(8)を式(6)に代入してR2を消去すると、次の式が得られます。
この式には、R1が分子と分母の両方に出てくるので、約分できて、R1も消去できる事に注意してください。
同様に、式(8)を式(7)に代入すると、次の式が得られます。
式(9)と式(10)に示す様に、分圧比の最小値αminと分圧比の最大値αmaxが、抵抗値の誤差εと設計上の分圧比のαtypの関数として表現できました。
お膳立てが終わったので、抵抗値の許容誤差を5%および10%として、αminおよびαmaxとαtypの関係をグラフで図示してみましょう。抵抗値の許容誤差が5%の時のグラフを図19に、許容誤差が10%の時のグラフを図20に示します。
分圧比の典型値とは、抵抗値に誤差がない場合の分圧比、すなわち設計上の分圧比の事を指します。
αminとαmaxは、共にεおよびαtypの関数の関数なので、それぞれαmin(ε,αtyp)およびαmax(ε,αtyp)と表記する事にすると、次の関係式が成立します。
この式は、図19や図20のグラフにおいて、水平座標と垂直座標が共に0.5の点を中心にαminやαmaxの曲線を180°回転させると、回転後のαminの曲線は回転前のαmaxの曲線に重なり、回転後のαmaxの曲線は回転前のαminの曲線に重なる事を意味します。(図21参照) この対称性は、キーパッドのノイズマージンを最大化する設計の上で、重要な性質になります。
また図19と図20を比較すると、当然の事ながら、抵抗値の許容誤差の大きい図20の方が、分圧比の最小値と最大値の差が大きくなっています。
また、いずれのグラフでも、設計上の分圧比αtypが0.5になる付近で、αminとαmaxの差が大きくなっており、逆にαtypが0付近または1付近では、αminとαmaxの差が小さくなっています。
分圧比の最小値と最大値の差についてもう少し細かく検討するために、それらの差をαdiffと定義します。式で書くと、次の様に定義します。
この式に、式(9)と式(10)を代入して計算すると、次の式が得られます。
αdiffをαtypで偏微分すると、次の式が得られます。
0<ε<1である事と、0≦αtyp≦1である事に注意すると、αtyp<0.5の時は∂αdiff∂αtyp>0となり、αtyp=0.5の時は∂αdiff∂αtyp=0となり、αtyp>0.5の時は∂αdiff∂αtyp<0となる事が分かります。つまり、許容誤差εの値を固定すると、αtyp=0.5の時に、αdiffは最大になります。
注意:αtyp=0.5の時に、αdiff=αmax−αminは最大になりますが、αtyp=0.5の時にαmax−αtypやαtyp−αminが最大になる訳ではありません。
また、αdiffはεとαtypの関数ですから、αdiff(ε,αtyp)と表記する事にすると、次の2式が成立します。
式(15)からは、εの値を固定して、αdiffとαtypの関係をグラフに書くと、αtyp=0.5の線を軸として、左右対称のグラフになる事が分かります。
式(16)からは、εの値を固定すると、αtyp=0.5の時に取るαdiffの最大値が、εになる事が分かります。
例えば、許容誤差5%の抵抗を使うと、設計上の分圧比が0.5の時(R1=R2の時)の、分圧比の最大値から最小値を引いた値が0.05になります。αtyp≠0.5の場合は、分圧比の最大値から最小値を引いた値は0.05より小さくなります。この知識は、抵抗値の誤差がどの程度分圧比に影響するかを、おおざっぱに見積もる際に役に立ちます。
抵抗値の許容誤差が5%(ε=0.05)の場合と10%(ε=0.1)の場合について、設計上の分圧比αtypが変化した時に、それに応じてαdiffがどの様に変化するかをグラフ化したものを、それぞれ図22と図23に示します。
これらのグラフを見ると、αdiffはαtyp=0.5の所を中心に、左右対称のグラフになっている事が分かります。また、αdiffはαtyp=0.5において、最大値ε(図22の場合は0.05で図23の場合は0.1)を取る事も分かります。
このページでは、抵抗値の誤差が、分圧比に対してどの様な影響を与えるかを解説しました。次回は、このページで説明した事柄を利用し、抵抗分圧式のキーパッドのノイズマージンを最大にするには、各抵抗値をいくらに設定すればいいかについて解説する予定です。続きを書くのはぼちぼちと。
 |
商品名 | I/Oピン一つで読める4X4キーパッドキット |
| 税抜き小売価格 | 900円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッドキットサポートページ |
 |
商品名 | I/Oピン一つで読める4X4キーパッド(完成品) |
| 税抜き小売価格 | 1380円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X4キーパッド(完成品)サポートページ |
 |
商品名 | I/Oピン一つで読める4X5キーパッドキット |
| 税抜き小売価格 | 2400円 | |
| 販売店 | スイッチサイエンス | |
| サポートページ | I/Oピン一つで読める4X5キーパッドキットサポートページ |
