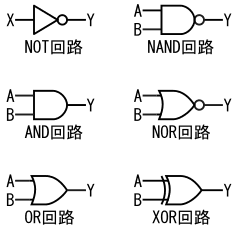
各回路において、X、A、およびBは、入力信号を表しています。またYは、出力信号を表しています。
| 2019年06月17日 | 更新。 |
組み合わせ回路(combinational circuit)あるいは組み合わせ論理回路(combinational logic circuit)とは、入力信号が決まれば、それに対して出力信号が一意的に決まる論理回路の事です。NOT回路、AND回路、OR回路などの基本論理回路は、組み合わせ回路の代表的な例です。
組み合わせ回路や組み合わせ論理回路という用語は、組み合わせ論理(combinatory logic)という、別の意味の用語と混同されやすいので注意が必要です。
以下に組み合わせ回路の例を示します。
基本論理回路は、全て組み合わせ回路です。図1に、基本論理回路の回路記号を示します。
また例として、AND回路の真理値表を表1に示します。この真理値表から、2つの入力信号AとBの値が決まれば、出力信号Yの値が一意的に決まる事が分かります。
| 入力電圧 | 出力電圧 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | L |
| H | L | L |
| H | H | H |
出力信号が複数ある組み合わせ回路の例として、半加算回路(半加算器)を紹介します。半加算回路の回路記号を図2に、真理値表を表2に示します。

半加算回路の回路記号を明確に定めたルールはないので、この図は半加算回路の回路記号の一例にすぎません。AとBは入力信号で、SとCは出力信号です。この回路記号の中央にHAと書いてあるのは、半加算回路を英語でHalf Adderと呼ぶ事に由来しています。
| 入力電圧 | 出力電圧 | ||
|---|---|---|---|
| A | B | C | S |
| L | L | L | L |
| L | H | L | H |
| H | L | L | H |
| H | H | H | L |
表2の真理値表を見て分かる様に、半加算回路も、入力信号AとBが決まれば、出力信号SとCが一意的に決まります。
半加算回路は、AND回路とXOR回路を組み合わせて、図3の様な回路で構成できます。
図3の例に示す様に、基本論理回路を適切に組み合わせると、さらに複雑な組み合わせ回路を構成する事ができます。
注:基本論理回路を組み合わせると、どんな論理回路でも構成できますから、基本論理回路を組み合わせて、さらに複雑な組み合わせ回路を構成できるのは当然の事です。しかし、ここで注意したいのは、後述する様に、基本論理回路の組み合わせ方によっては、組み合わせ回路にならない場合がある事です。
組み合わせ回路の意味をさらに明確に理解するために、以下に組み合わせ回路ではない回路の例を示します。
現在の入力信号だけではなく、過去の回路の状態が出力信号に影響する回路があります。この様な回路を順序回路(sequential circuit)といいます。言い方を変えれば、順序回路は情報を記憶する作用のある回路とも表現できます。
参考:過去の回路の状態は、回路の初期状態(電源投入直後の状態)と、過去の入力信号により決まります。
順序回路という言葉の定義より明らかな様に、順序回路は組み合わせ回路ではありません。
代表的な順序回路として、RSフリップフロップを紹介します。
RSフリップフロップとは、2つの入力信号RおよびSと、2つの出力信号QおよびQを持つ論理回路で、RにH、SにLを入力した場合は0を記憶し、RにL、SにHを入力した場合は1を記憶し、RとSの両方にLを入力した場合は記憶内容を保持する働きを持つ、1ビットの記憶回路の事です。0を記憶している状態ではQにL、QにHを出力し、1を記憶している状態ではQにH、QにLを出力します。
参考:RSフリップフロップのRとSの両方にHを入力する事は禁止される(利用者にRとSに同時にHを入力しない義務を課す)場合が多いです。
図4がRSフリップフロップの回路図です。また、RSフリップフロップの真理値表を表3に示します。
| 入力電圧 | 出力電圧 | 動作 | ||
|---|---|---|---|---|
| R | S | Q | Q | |
| L | L | QOLD | QOLD | 記憶保持 |
| L | H | H | L | セット(1を記憶させる) |
| H | L | L | H | リセット(0を記憶させる) |
| H | H | L | L | 禁止 |
表3にはQOLDという信号名が使われていますが、これは出力信号Qの直前の値を意味しています。またQOLDは、QOLDを論理反転した値を意味しています。
RSフリップフロップには図5に示すNOR回路を2つ使っています。そこで、NOR回路の動作を振り返るために、NOR回路の真理値表を表4に示します。
| 入力電圧 | 出力電圧 | |
|---|---|---|
| A | B | Y |
| L | L | H |
| L | H | L |
| H | L | L |
| H | H | L |
ここで、NOR回路の一方の入力のBをVCC(電源電圧)につないで、入力する電圧をHに固定する場合を考えてみます。表4より、BにHを入力した場合は、Aの入力値にかかわらず、NOR回路はLを出力する事が分かります。よってこの場合、図6の様な等価回路になります。
先程とは逆に、入力BをGND(基準電位、0V)につないで、入力する電圧をLに固定する場合を考えてみます。表4より、BにLを入力した場合は、NOT回路はAを論理反転(NOT)した値をYに出力する事が分かります。よってこの場合、図7の様な等価回路になります。
これらのNOR回路の性質を踏まえた上で、RSフリップフロップの動作について考察し、図4のRSフリップフロップにおいて表3の真理値表が得られる事を確認してみましょう。
図6と図7の等価回路を用いて、RにL、SにHを入力した場合のRSフリップフロップの等価回路を求めると、図8の様になります。
図8を見ると分かる様に、RにL、SにHを入力した場合には、RSフリップフロップはQにH、QにLを出力します。これは、RSフリップフロップに1という情報を記憶させる操作に相当します。
この様な、RSフリップフロップに1を記憶させる操作の事をセット(set)と呼びます。セット時には、RSフリップフロップの出力信号(QとQ)は一意的に決まります。
今度は、RにH、SにLを入力した場合に、RSフリップフロップがどのように振舞うかを考察します。
図6と図7の等価回路を用いて、RにH、SにLを入力した場合のRSフリップフロップの等価回路を求めると、図9の様になります。
図9を見ると分かる様に、RにH、SにLを入力した場合には、RSフリップフロップはQにL、QにHを出力します。これは、RSフリップフロップに0という情報を記憶させる操作に相当します。
この様な、RSフリップフロップに0を記憶させる操作の事をリセット(reset)と呼びます。リセット時にも、RSフリップフロップの出力信号(QとQ)は一意的に決まります。
今度は、RとSの両方にLを入力した場合に、RSフリップフロップがどのように振舞うかを考察します。
図7の等価回路を用いて、RとSの両方にLを入力した場合のRSフリップフロップの等価回路を求めると、図10の様になります。
図10の右側の等価回路からだけでは、2つの出力(QとQ)の電圧が確定しません。というのは、この回路には、図11と図12に示す様に、安定状態が2つ存在するからです。
図11の状態においても、図12の状態においても、2つのNOT回路の入力端子と出力端子とでは、論理が反転している事が分かります。よって、RとSの両方にLを入力した場合に、図11の状態になろうとも、図12の状態になろうとも、矛盾は発生ないのです。
RとSの両方にLを入力した状態では、図11の状態になるにせよ、図12の状態になるにせよ、一度状態が確定すると、その後もその状態を保持する様に働きます。この動作を記憶保持と呼びます。
それでは、図11の状態になるか、図12の状態になるかを決める要素は何でしょうか?それは、RとSの両方にLを入力する様になる直前の回路の状態なのです。
もし、RSフリップフロップをセットした状態(図8の状態)から、記憶保持状態に移行したなら、RSフリップフロップは、セット時のQ=H、Q=Lの状態を維持します。(つまり、図11の状態に移行します。)
もし、RSフリップフロップをリセットした状態(図9の状態)から、記憶保持状態に移行したなら、RSフリップフロップは、リセット時のQ=L、Q=Hの状態を維持します。(つまり、図12の状態に移行します。)
この様に、RSフリップフロップの出力信号の値は、入力信号の値からだけで決まるわけではなく、過去の回路の状態によっても決まります。つまり、RSフリップフロップは順序回路であり、組み合わせ回路ではありません。
前述したとおり、RとSの両方にHを入力する事は、禁止される場合が多いのですが、表3の真理値表が正しい事を確かめるために、RとSの両方にHを入力した場合のRSフリップフロップの振る舞いについても考えてみます。
図6の等価回路を用いて、RとSの両方にHを入力した場合のRSフリップフロップの等価回路を求めると、図13の様になります。
この等価回路から、QとQの両方の出力がLになる事が分かります。
余談:RとSの両方にHを入力した(禁止状態にした)後、同じタイミングでRとSの両方をLにした(記憶保持状態へ遷移した)場合、図11と図12のどちらの安定状態になるかは、理論的には予想できません。この場合、どちらの安定状態になるかを決める要因は、2つのNOR回路の閾値のばらつきなど、回路素子の微妙な特性の違いや雑音などになります。また、安定状態になる前に、短時間だけ回路が発振したり、LともHともつかない中間の電圧を出力する事もあります。(メタステーブル) RとSの両方にHを入力する事を禁止するのは、出力値が理論的に予想できない事態やメタステーブルを回避するためという理由があります。また、RとSの両方にHを入力すると、Qを論理反転した信号がQにならないという理由もあります。禁止状態から直接記憶保持の状態に遷移する事を認めると、RSフリップフロップは厳密には順序回路とは呼べなくなります。
先ほど順序回路が組み合わせ回路ではない事を説明しましたが、順序回路以外にも、組み合わせ回路ではない回路が存在します。
入力信号を一定値にしても(入力信号が時間的に変化しない様にしても)、出力信号が一定値にはならず、変化し続ける回路があるのです。
例えば図14の回路について考えてみます。
図6の等価回路を使って、図14の回路のXにHを入力した場合の等価回路を考えると、図15の回路が得られます。
図15の等価回路を見ると分かる様に、図14の回路のXにHを入力した場合、YにはLが出力されます。
今度は図7の等価回路を使って、図14の回路のXにLを入力した場合の等価回路を考えると、図16の回路が得られます。
図14の回路のXにLを入力した場合、図16の右の図に示す様に、NOT回路が3個、環状に接続された回路が等価的に生成されます。この回路はリング発振器と呼ばれ、高い周波数の方形波を出力します。つまり、出力Yの値は、短い周期でHとLを繰り返します。
図15と図16の等価回路を踏まえて、ある時点までXにHを入力し、その時点以降はXにLを入力した場合の図13の回路のタイミングチャートの例を描くと、図17の様になります。
この様に、入力信号の値が時間的に変化しないにもかかわらず、出力信号の値がいつまでも変化し続ける状態になる現象を発振といいます。
参考1:回路に入力端子がないにもかかわらず、出力信号の値がいつまでも変化し続ける状態になる事も発振といいます。(入力端子がなければ、そもそも入力信号の値が時間的に変化しようがありません)
参考2:発振している出力信号の電圧波形は、通常は、周期を持った繰り返し波形になりますが、複雑な回路においては、周期のないカオス的な出力波形になる可能性もあります。
発振現象を起こす回路は、しばしば設計の失敗した回路だとみなされますが、場合によっては、リング発振器の様に意図的に発振現象を起こす様に設計された回路もあります。この様な回路を発振回路あるいは発振器と呼びます。
組み合わせ回路の場合は、入力信号がある値に定まると、出力信号は一意的に定まりました。
順序回路の場合は、入力信号がある値に定まったとしても、出力信号は過去の回路の状態に影響を受けるので、一意的には定まりませんでした。ただし、出力信号が一意的には定まらないといっても、入力信号に時間的変化がなければ、出力信号にも時間的変化はありませんでした。
図14の回路の様に発振現象を起こす回路は、入力信号が時間的に変化しなくても、出力信号が永遠に変化し続ける(場合がある)ので、組み合わせ回路にも順序回路にも分類されません。
注:組み合わせ回路や順序回路において、入力信号がある値に定まると、出力信号も定まり、時間的に変化しなくなるというのは、回路素子の伝搬遅延時間を無視した場合の話です。伝搬遅延時間が無視できない現実の回路においては、入力信号が時間的に変化しなくなっても、その後わずかな時間においては、出力信号が変化します。しかし、発振現象を起こす回路の様に、出力信号の時間的変化が永遠に続くという事はありません。
