| 2020年04月14日 | 更新 |
論理回路において、「ボタンが押された」、「起動後一定の時間が経過した」、「センサが異常を検出した」など、何かが起こった時や、何かをこれからしなければならない等の状況で電圧がHになり、それらの条件が成立しない時には電圧がLになる信号を、正論理(positive logic)の信号といいます。逆に、何かが起こった時や、何かをこれからしなければならない等の状況で電圧がLになり、それらの条件が成立しない時には電圧がHになる信号を、負論理(negative logic)の信号といいます。
注:ここでHは、閾値より高い信号電圧を表しています。またLは、閾値より低い信号電圧を表しています。
正論理は、意味のある現象が起こった時に高い電圧が出る信号の方式なので、アクティブハイ(active high)ともいわれます。また負論理は、意味のある現象が起こった時に低い電圧が出る信号の方式なので、アクティブロー(active low)ともいわれます。
正論理と負論理は、対比する形で説明すると意味が把握しやすいため、このページでは負論理だけでなく、正論理についても説明します。
先ほど、正論理とは意味のある現象が起こった時に電圧Hを出力し、意味のある現象が起こらなかった時は電圧Lを出力する信号の方式の事だと説明しました。別の言い方をすると、正論理は、真理値0を電圧Lに対応させ、真理値1を電圧Hに対応させる、真理値と電圧の対応方法だといえます。この事を表したのが表1です。
| 真理値 | 電圧 |
|---|---|
| 0 (偽) | L |
| 1 (真) | H |
注:論理学において命題が「真」(T)である事を論理回路では2進数の"1"で表し、論理学において命題が「偽」(F)である事を論理学では2進数の"0"で表します。
逆に負論理は、真理値0を電圧Hに対応させ、真理値1を電圧Lに対応させる、真理値と電圧の対応方法だといえます。この事を表したのが表2です。
| 真理値 | 電圧 |
|---|---|
| 0 (偽) | H |
| 1 (真) | L |
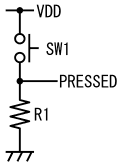
正論理信号を発生する回路の簡単な例として、押しボタンスイッチのボタンが押されている時(ONになっている時)はH、ボタンが押されていない時(OFFになっている時)はLになる信号、PRESSEDを発生する回路を図1に示します。
この回路は、押しボタンスイッチSW1と抵抗R1から構成されています。SW1とR1は直列接続されていますが、それらが接続されている部分の電圧を取り出したのが、PRESSEDという信号です。
参考1:電子回路設計の分野では、信号あるいは信号線には、図1のPRESSEDの様に、英数字の文字列で名前を付ける習慣があります。通常アルファベットには大文字を使いますが、小文字を使う場合もあります。また英数字だけではなく、"_"、"/"、"#"等の記号を信号名(信号の名称)に使う場合もあります。
参考2:"PRESSED"は、「押されている」という意味の英単語です。この様に、信号名には、意味の推測できる英単語、またはその略語を使うのが習慣になっています。
図1の回路においてVDDとは、論理回路を動かすための正の電源電圧を表しています。
ボタンが押されていない場合(SW1がOFFの場合)は、PRESSED信号は、抵抗R1によってGNDにプルダウンされているため、出力電圧が0[V]、すなわちLになります。
一方でボタンが押されている場合(SW1がONの場合)は、PRESSED信号は、SW1経由でVDDにショートされるため、出力電圧がVDD、すなわちHになります。
PRESSED信号の表す命題(真偽が明確に定められる事柄)が「ボタンが押されている」事だとすると、真理値と電圧の関係は表3の様になります。
| 真理値 | 電圧 |
|---|---|
| 0 (偽) | L |
| 1 (真) | H |
注:真理値が0(偽)の場合は、「ボタンが押されている」という命題が成立しなかった、すなわちボタンが押されていない事を意味します。一方で真理値が1(真)の場合は、命題が成立した、すなわちボタンが押されている事を意味します。
表3から分かる様に、真理値0は電圧Lに対応しており、真理値1は電圧Hに対応しているので、確かにPRESSED信号は正論理の信号であるといえます。
次に、負論理信号を発生する回路の簡単な例として、押しボタンスイッチのボタンが押されている時(ONになっている時)はL、ボタンが押されていない時(OFFになっている時)はHになる信号、PRESSEDを発生する回路を図2に示します。
信号名PRESSEDには、上線が付いていますが、この様に、負論理の信号の信号名には、上線を付ける習慣があります。
注:ただし、あくまでも習慣なので、必ず負論理の信号名に上線を付けなければならない訳ではありません。信号名に上線を付けない場合は、その信号が負論理の信号である事を、別の手段で説明する必要があります。
図2の回路も押しボタンスイッチSW1と抵抗R1から構成されていますが、SW1とR1の位置関係が、図2の回路と図1の回路では、上下逆になっています。
図2の回路でボタンが押されていない場合(SW1がOFFの場合)は、PRESSED信号は、抵抗R1によりVDDにプルアップされているため、出力電圧がVDD、すなわちHになります。
一方でボタンが押されている場合(SW1がONの場合)は、PRESSED信号は、SW1経由でGNDにショートされるため、出力電圧が0[V]、すなわちLになります。
PRESSED信号の表す命題が、図1のPRESSED信号の場合と同様に「ボタンが押されている」事だとすると、真理値と電圧の関係は表4の様になります。
| 真理値 | 電圧 |
|---|---|
| 0 (偽) | H |
| 1 (真) | L |
表4から分かるように、真理値0は電圧Hに対応しており、真理値1は電圧Lに対応しているので、確かにPRESSED信号は負論理の信号であるといえます。
正論理回路と負論理回路とでは、AND回路とOR回路が入れ替わる現象があるので、説明します。
AND回路とは、2つの入力が共に1の場合は出力が1になり、それ以外の場合は出力が0になる、2入力1出力回路と定義されています。
注:3入力以上のAND回路もありますが、ここでは2入力のAND回路のみを考えています。
よって、AND回路の2つの入力信号の信号名をAとBとし、出力信号の信号名をYとすると、真理値表は表5の様になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
A、B、およびYが全て正論理の信号だとすると、AND回路の電圧表記の真理値表は、表5中の0をL、1をHに書き換えれば得られます。その結果を表6に示します。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | L |
| H | L | L |
| H | H | H |
表6の真理値表に従って動作する正論理のAND回路は、図3の様な回路記号で表わす事になっています。
ここで、A、B、およびYが全て負論理の信号だとすると、AND回路の電圧表記の真理値表は、表5中の0をH、1をLに書き換えれば得られます。また、信号が負論理になった事が分かりやすい様にするには、A、B、Yのそれぞれの信号名に上線を付けて、A、B、Yとする方がいいでしょう。その結果を表7に示します。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| H | H | H |
| H | L | H |
| L | H | H |
| L | L | L |
この表の行の順番を入れ替えて見やすくすると、表8の様になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | H |
| H | L | H |
| H | H | H |
表8は、正論理のOR回路(図4参照)の真理値表(表9参照)と、(A、B、YがそれぞれA、B、Yになっている所を除いて)一致します。つまり、負論理のAND回路は、物理的には正論理のOR回路と同じ回路なのです。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | H |
| H | L | H |
| H | H | H |
正論理のOR回路と同じ働きをするからといって、負論理のAND回路を、図5の様に正論理のOR回路の回路記号で表したのでは、AND回路である事が分かりにくいので、負論理のAND回路を図6の回路記号で表わす習慣があります。
注:ただし負論理のAND回路を、図5に示す様に、正論理のOR回路の回路記号で書いても間違いではありません。
図6をみると分かる様に、負論理のAND回路の回路記号は、正論理のAND回路の回路記号の入力端子と出力端子に、全て丸印が付いています。
この丸印は、NOT回路を表しています。つまり、図6の回路記号は、図7の回路の省略記法だと考える事もできます。
参考:NOT回路は正論理の信号を負論理に変換したり、負論理の信号を正論理に変換したりできます。正論理の信号を負論理に変換する場合には図8の回路記号を、負論理の信号を正論理に変換する場合には図9の回路記号を使う習慣があります。負論理側の端子に丸印を付けると覚えれば、覚えやすいでしょう。(さらに詳しい話は、NOT回路の項目をご覧ください)
図7の回路の2つの負論理の入力信号AとBはそれぞれ、NOT回路で正論理信号AとBに変換された後、正論理のAND回路に入力されます。正論理のAND回路の出力信号Yは、NOT回路で負論理の信号Yに変換されて出力されます。
この様に、図6の回路記号は、正論理のAND回路の入力端子に、正論理を負論理に変換するNOT回路が付いており、出力端子には、正論理を負論理に変換するNOT回路が付いている様子を表しているのです。
前の項では、負論理のAND回路が正論理のOR回路と物理的には同じ回路になる事を説明しましたが、この項では、逆に、負論理のOR回路が正論理のAND回路と物理的に同じになる事を説明します。
OR回路とは、2つの入力の少なくとも一方が1の場合は出力が1になり、それ以外の場合は出力が0になる回路と定義されています。
注:3入力以上のOR回路もありますが、ここでは2入力のOR回路のみを考えています。
よって、OR回路の2つの入力信号の信号名をAとBとし、出力信号の信号名をYとすると、真理値表は表10の様になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
A、B、およびYが全て正論理の信号だとすると、OR回路の電圧表記の真理値表は、表10中の0をL、1をHに書き換えれば得られます。その結果を表11に示します。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | H |
| H | L | H |
| H | H | H |
注:表11は、表9と同じ表です。
表11の真理値表に従って動作する正論理のOR回路を、図4の回路記号で表わす事は既に説明しました。
今度は表10のA、B、およびYが、全て負論理の信号の場合を考えます。
負論理の場合は、表10中の0をH、1をLに書き換えれば電圧表記の真理値表が得られます。その際に、負論理信号である事が分かりやすい様にするために、3つの信号名A、B、Yを、それぞれA、B、Yと書き直す方がいいでしょう。この様にして得られた真理値表を表12に示します。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| H | H | H |
| H | L | L |
| L | H | L |
| L | L | L |
表12の行を入れ替えて見やすくすると、表13の真理値表が得られます。
| 入力 | 出力 | |
|---|---|---|
| A | B | Y |
| L | L | L |
| L | H | L |
| H | L | L |
| H | H | H |
この真理値表は、表6に示した正論理のAND回路の真理値表と、(A、B、YがそれれぞれA、B、Yとなっている所を除いて)一致します。つまり、負論理のOR回路は、物理的には正論理のAND回路と同じ回路なのです。
正論理のAND回路と同じ働きをするからといって、負論理のOR回路を、図10の様に正論理のAND回路の回路記号で表わしたのでは、OR回路である事が分かりにくいので、負論理のOR回路を図11の記号で表わす習慣があります。
注:ただし負論理のOR回路を、図10に示す様に、正論理のAND回路の回路記号で書いても間違いではありません。
