前回は、注目する点がちょうど円弧上にあった時に、その点が1/4円の内部にあると解釈するべきか、外部にあると解釈するべきかという、細かい点について説明しました。
今回は、いよいよ整数演算だけで円周率を計算するプログラムを作ってみます。
単純に R 2個のコマ全てについて1/4の内部にあるかどうかを判定するプログラム
面積が1の R 2個のコマ全てについて、原点に中心があって半径が R の1/4円の内部にあるか、外部にあるかを判定し、1/4円の内部のコマの数から円周率を求めるプログラムを作ります。
積極的な手法と消極的な手法について振り返る
1/4円の内部にあるコマを数えるにあたっては、コマの左下の隅が1/4円の内部であれば、コマが1/4円の内部にあると考える積極的な手法と、コマの右上の隅が1/4円の内部であって初めて、コマが1/4円の内部にあると考える消極的な手法により円周率を求めます。
実際の円周率は、積極的な手法で推定した円周率と、消極的な手法で推定した円周率の間にある事が、理論的に保証されます。
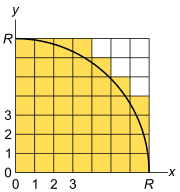
積極的な手法の場合は、 x と y をそれぞれ0~ R −1の範囲で変化させ、座標( x , y )が1/4円の内部にあるか、外部にあるかを判定する事になります。( x , y )がちょうど1/4円の円弧上にある場合は、( x , y )は1/4円の外部にあると判定します。
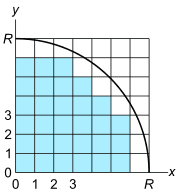
消極的な手法の場合は、 x と y をそれぞれ1~ R の範囲で変化させ、座標( x , y )が1/4円の内部にあるか、外部にあるかを判定する事になります。( x , y )がちょうど1/4円の円弧上にある場合は、( x , y )は1/4円の内部にあると判定します。
点( x , y )が1/4円内にあるかどうかの判定法
前前回にも紹介したとおり、第1象限の点(x,y)が、中心が原点で半径が R の1/4円内にあるかどうかは、次の表に示す判定法で判定できます。
| 条件 | 判定 |
|---|---|
| y > ( R 2 − x 2)0.5 | 点( x , y )は1/4円の外部にある |
| y = ( R 2 − x 2)0.5 | 点( x , y )は1/4円の円弧上にある |
| y < ( R 2 − x 2)0.5 | 点( x , y )は1/4円の内部にある |
ただこの判定法では、平方根の計算が必要となり、浮動小数点の、時間のかかる計算が必要になります。
そこで、等式あるいは不等式の両辺を2乗して、次の様な判定法に改めると、整数の掛け算(2乗の計算は同じ数同士の掛け算と考える)と引き算しか出てこない、高速な判定ができます。
| 条件 | 判定 |
|---|---|
| y 2 > R 2 − x 2 | 点( x , y )は1/4円の外部にある |
| y 2 = R 2 − x 2 | 点( x , y )は1/4円の円弧上にある |
| y 2 < R 2 − x 2 | 点( x , y )は1/4円の内部にある |
C言語でのプログラム例
この様な方針で1/4円の面積を求め、その面積から円周率の推定値を求めるプログラムをC言語で作ると、次の様になります。
#include <stdio.h>
#include <stdint.h>
int main(void){
const uint32_t R=10000U; // 1/4円の半径。大きくするほど円周率が精度よく求まる。
uint32_t x,y;
uint32_t s1; // 積極的な手法で求めた円周率の面積
uint32_t s2; // 消極的な手法で求めた円周率の面積
// 積極的な手法で1/4円の面積を求める
s1=0;
for(x=0; x<R; x++) { // xを0~R-1の範囲で変化
for(y=0; y<R; y++) { // yを0~R-1の範囲で変化
if(y*y<R*R-x*x) s1++;
} // for y
} // for x
// 消極的な的な手法で1/4円の面積を求める
s2=0;
for(x=1; x<=R; x++) { // xを1~Rの範囲で変化
for(y=1; y<=R; y++) { // yを1~Rの範囲で変化
if(y*y<=R*R-x*x) s2++;
} // for y
} // for x
// 1/4円の面積を4/(R*R)倍して円周率を求める
printf("max:%1.14f\n",s1*4.0/(R*R));
printf("min:%1.14f\n",s2*4.0/(R*R));
printf("ave:%1.14f\n",(s1+s2)*2.0/(R*R));
} // max
1/4円の面積を求める部分については、 整数の掛け算、足し算、および引き算のみでプログラムを組めています。
1/4円の面積を4/ R 2倍して円周率を換算する部分については、浮動小数点演算を使っています。
ただし、R を2のべき乗に設定した場合は、 R 2で割る操作は2進数の小数点を左に移動する操作に相当します。つまり、2進数の固定小数点演算をする場合は、実質的には割り算の演算が不要です。
また、R を10のべき乗に設定した場合は、 R 2で割る操作は10進数の小数点を左に移動する操作に相当します。つまり、BCD符号を使うなど、 10進数の固定小数点演算をする場合は、実質的には割り算の演算が不要です。
先ほどのプログラムをpaiza.IOで動作させられるようにしたのが、次の画面です。
半径 R を10000に設定して実行すると、max(積極的な手法で推測した円周率)が3.14199016、min(消極的な手法で推測した円周率)が3.14119052となっており、それらの平均のaveが3.14159034と求まります。aveを正確な円周率の3.14159265・・・と比較すると、円周率が6桁計算できている事が分かります。
なお、上の画面中で、Rの値を10000U(末尾のUはunsignedの意味)とは別の値に書き換えて実行すると、半径Rを変えて計算できます。
ただpaiza.IOには、コンパイルと実行の時間が2秒以内という制約があるため、Rを大きくしすぎると、タイムアウトしてしまいます。R=50000Uで試すと実行できましたが、 R=60000Uではタイムアウトしてしまいます。 もっとRを大きくして円周率を高精度で求めたい場合は、アルゴリズムを改良して、高速化する必要があります。
アルゴリズムを高速化するには
今回紹介したプログラムでは、1/4円の面積を計算するのに、 R 2個のコマについて、1/4円の内部にあるかどうかを判定していました。そのため、(積極的な手法と消極的な手法の双方で) R 2回の計算が必要でした。
本当にそんなに多くの回数の計算が必要なのでしょうか? R が1万の時は、1億回の計算をする事になってしまいます。(それを実際に2秒以内に実行するPaiza.IOはすごいです)
実は、次の様な点に注目すれば、もっと計算回数を減らす事ができます。
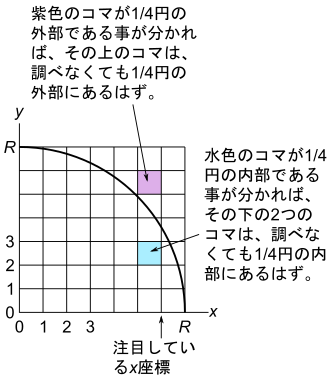
上の図は、消極的な手法で1/4円内部のコマの数を数えている一場面を表しています。特定のx座標に注目し、同じx座標の列の中に、1/4円内部のコマがいくつあり、1/4円内部のコマがいくつあるかを調べています。
もし、水色のコマが1/4円の内部にあると先に判定したら、その下2つのコマは、数式により1/4円の内部にあると判定しなくても、当然1/4円の内部にあるはずです。
もし、紫色のコマが1/4円の外部にあると先に判定したら、その上1つのコマは、数式により1/4円の外部にあると判定しなくても、当然1/4円の外部にあるはずです。
これらの事から、うまくやれば、1列全てのコマについて1/4円の内部にあるか、外部にあるかを判定しなくても、もっと少ないコマを判定するだけで、その列にある1/4円内のコマ数を数える事ができそうです。
当然、1/4円の内部にあるか外部にあるかを判定するコマの数が減れば、プログラムは高速化します。
この様なアイデアを積極的に利用すると、プログラムが劇的に高速化するのですが、説明が長くなってきたので、詳細は次回に説明します。