前回から、整数の足し算と引き算だけで円周率の近似値を求めるアルゴリズムについて解説しています。
多くの桁を高速で求めるのに適したアルゴリズムではないものの、整数の足し算と引き算しか出てこないので、ハードウェアに実装する場合に、部品数が少なくて済むというメリットがあります。今回はそこまで踏み込みませんが、HDLを使ってFPGAなどに実装するのも容易です。
前回は、この連載で説明しているアルゴリズムが、1/4円の面積を、定積分の近似計算で求めている事を説明しました。また、定積分の近似計算を、浮動小数点を使って行うプログラムを例示しました。
今回は、整数演算だけで、ほぼ同様の計算ができる事を説明します。
前回紹介した浮動小数点のプログラムの問題点
前回は、半径 R の1/4円を表す数式であるy = ( R 2– x 2)0.5を、0から R の範囲で x で定積分すると、計算結果がπ R 2/4になる事を利用して、円周率の近似値を計算できる事を説明しました。
また R が整数の場合について考え、定積分の範囲を幅1の R 個の区間に分け、それぞれの区間において、円弧と x 軸が囲む面積を長方形で近似する事により、定積分を近似計算するプログラムの例を挙げました。
前回の記事を読み返さなくてもいい様に、定積分の近似計算のアイデアを書いた図と、例示したC++のプログラムを、以下に再掲します。
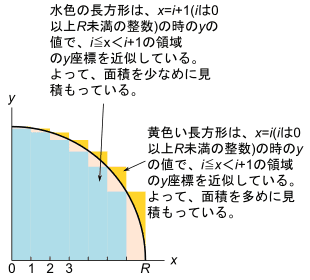
実行結果の maxは、黄色の長方形の面積の和で求めた円周率で、実際の円周率は、このmaxよりも必ず小さくなります。またminは、図の水色の長方形の面積の和で求めた円周率で、実際の円周率は、このminよりも必ず大きくなります。aveは、minとmaxの平均値で、円周率の推測値になります。
これで円周率の近似計算を行えるようにはなったのですが、浮動小数点で計算している所や、平方根の計算をしている所などが不満です。パソコンで計算する場合も、これらの重い計算が含まれていると、実行時間が長くなります。またハードウェアに実装する場合は、部品数が増えてしまいます。
整数計算によるアルゴリズム
そこで、浮動小数点の計算を排除し、整数だけで定積分を行う方法を考えます。また、同時に平方根の計算をしないで済む方法も考えます。
領域を y 軸方向にも R 個に分割する
前回、定積分を数値計算するために、積分区間を x 軸方向に R 個に分割する話をしました。
今回は、図形を x 軸方向に加え、 y 軸方向にも R 個に分割します。この操作により、定積分の近似精度が若干下がるものの、整数だけで計算できる様になります。
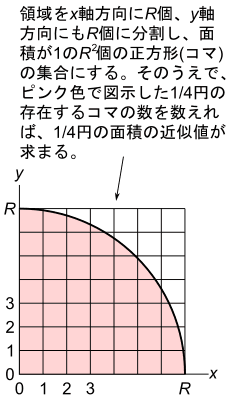
y 軸方向にも領域を分割するアルゴリズムの大まかな考え方を表したのが上の図です。
原点から x 軸方向に R 、 y 軸方向にも R の正方形の領域を、 x 軸方向にも y 軸方向にもそれぞれ R 個に分割し、面積が1の正方形のコマを R 2個作ります。そして、1/4円内にあるコマの数を数えれば、1/4円の面積の近似値が求まります。
1/4円内にあるコマの数を数える時に、コマ全体が1/4円内にある場合のみにコマを数える消極的な手法を取れば、1/4円の面積を小さめに見積もります。(下図の水色の領域)
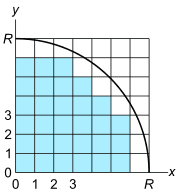
上の図は R =7の場合について作図した物ですが、水色のコマが30個あるので、半径7の1/4円の面積を30と見積もった事になります。半径7の1/4円の正確な面積はπ×72/4≒38.5ですから、確かに面積を8.5だけ小さめに見積もっています。
また、コマの一部にでも1/4円が入っていればコマを数える積極的な手法を取れば、1/4円の面積を大きめに見積もります。(下図の黄色の領域)
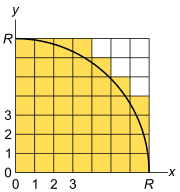
上の図の例では、黄色いコマが43個ありますので、半径7の1/4円の面積を43と見積もった事になります。正確な1/4円の面積よりも43-38.5=4.5だけ大きめに見積もっています。
せっかくCADで正確な図を描いたので、上の2つの図より、 R =7の場合について、円周率の近似値を計算してみましょう。
まず、水色コマで表わした消極的な手法でコマの数を数えたケースですが、1/4円の面積を30と見積もったので、これから円周率の近似値を計算すると、30×4/72≒2.449になります。あまり正確な数ではありませんが、これで円周率が2.449より大きい事が数学的に証明できたことになります。
次に、黄色のコマで表わした積極的な手法でコマの数を数えたケースですが、1/4円の面積を43と見積もったので、これから円周率の近似値を計算すると、43×4/72≒3.510になります。これで、円周率が3.510より小さい事が数学的に証明できた事になります。
なお、消極的な手法では必ず円周率を実際の値より小さく見積もり、積極的な手法では必ず円周率を実際の値より大きく見積もりますので、それらの値の平均を取れば、より真の円周率に近い値を推測できる事になります。
参考:消極的な手法で求めた円周率の近似値と、積極的な手法で求めた円周率の近似値の平均を取るという操作は、定積分の際に、1/4円の中に完全に収まっているコマの面積を1とし、1/4円の中に部分的に収まっているコマの面積は、(実際に1/4円に収まっている部分の面積が0~1の値を取るのを無視して、)一律0.5とみなして計算し、そうして求めた1/4円の面積から円周率を推測するという事に相当します。
実際に、消極的な手法と積極的な手法による円周率の推測値の平均を取ると2.980と、より実際の円周率(3.141592・・・)に近い値になっています。
参考:前回紹介した最初のプログラムを、Rを7に書き換えて実行すると、実際にmax:3.51020408163265、min:2.44897959183673、ave:2.97959183673469と、ここで紹介したのと同じ値が表示されます。前回の記事のページ上でプログラムを動作させられますので、興味がある方は、是非試してください。
R =7の場合では、あまり正確な円周率の値は出ませんでしたが、 R を大きな値に設定すると、積極的な手法で推測した円周率の値と消極的な手法で推測した円周率の値が近づき、より正確に円周率を推定できる様になります。
コマが1/4円内にあるかどうかを判定する方法
R が小さい値の場合は、先ほどの様にCADや精密な製図道具で正確な作図をし、各コマが半径 R の1/4の内部にあるかどうかを目で確認する事ができましたが、 R が大きくなると、正確な作図が困難になります。
この場合、数式により、純粋に数学的な手法で各コマが1/4円の内部にあるかどうかを判定する事になります。その際に、
- コマの全体が1/4円の内部にあるケース
- コマの全体が1/4円の外部にあるケース
- コマの一部が1/4円の内部にあるケース
の3種類を区別できないと、消極的な手法と積極的な手法を使い分けて、円周率の推測値の上限と下限を決める事ができません。
幸い、扱う関数が第1象限の1/4円弧と、単調減少の単純な関数のため、これから説明する方法で、前述の3つのケースを判別する事ができます。
コマの全体が1/4円の内部にあるかどうかの判定
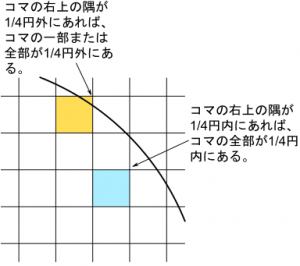
1/4円の円弧は単調減少関数( x が増えるほど y が減る関数)なので、コマの全体が1/4円内にあるかどうかは、コマの右上の隅の座標が1/4円内にあるかどうかを判定するだけで、コマ全体が1/4円内にある事を確認できます。(下図参照)
単調関数ではない一般の関数の場合、その関数の図形内にコマがあるかどうかは、コマ内のどこか1点が図形内にあるかどうかを調べても判断できませんので、厄介です。(下図参照)
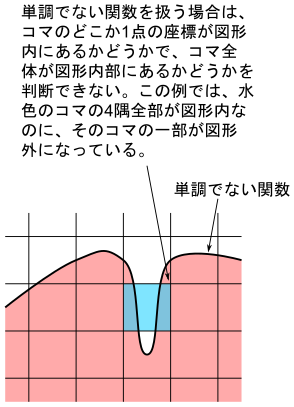
コマの全体が1/4円の外部にあるかどうかの判定
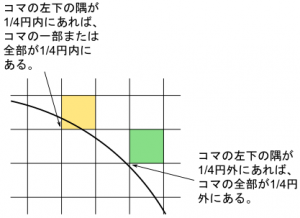
1/4円の円弧が単調現象関数である事を利用すると、コマの左下の隅の座標が1/4円の外部にあるかどうかで、コマの全体が1/4円の外部にあるか、コマの一部または全体が1/4円の内部にあるかが判定できます。(下図参照)
コマの一部が1/4円の内部にあるかどうかの判定
コマの左下の隅の座標が1/4円の内部にあり、かつ、コマの右上の隅の座標が1/4円の外部にあれば、そのコマは一部が1/4円の内部にあり、別の一部が1/4円の内部にあります。
もしこの条件が成立しなければ、コマの全部が1/4円の内部にあるか、またはコマの全部が1/4円の外部にあります。
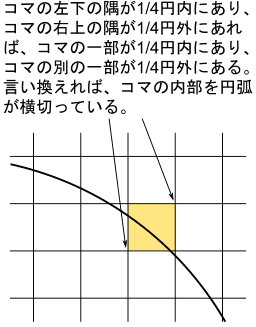
コマが1/4円の内部にあるか外部にあるかの判定法のまとめ
以上のように、コマの一部または全体が1/4円の内部にあるか、外部にあるかを判定するには、コマの左下隅および右上隅の座標が1/4円の内部にあるか、外部にあるかを調べればよい事が分かりました。この判定法を表にまとめると、次の様になります。
| コマの左下隅 | コマの右上隅 | 判定 |
|---|---|---|
| 1/4円の内部 | 1/4円の内部 | コマの全部が1/4円の内部 |
| 1/4円の内部 | 1/4円の外部 | コマの一部のみが1/4円の内部 |
| 1/4円の外部 | 1/4円の内部 | こういう事態は発生し得ない |
| 1/4円の外部 | 1/4円の外部 | コマの全部が1/4円の外部 |
ある1点の座標が1/4円の内部にあるかどうかの判定法
前節で、コマの左下隅と右上隅の座標が1/4円の内部にあるかどうかを調べれば、コマの一部または全部が、1/4円の内部にあるかどうかを判定できる事を説明しました。
次に、特定の座標(x,y)が与えられた時に、その点が1/4円の内部にあるかを調べる方法について考えます。
前回の式(2)で説明したとおり、半径Rの1/4円の円弧上の点は、次の式を満たします。
y = ( R 2– x 2)0.5 ・・・ (1)
よって、次の表に示す条件で、点( x , y )が1/4円の内部にあるか外部にあるかが判定できます。
| 条件 | 判定 |
|---|---|
| y > ( R 2 − x 2)0.5 | 点( x , y )は1/4円の外部にある |
| y = ( R 2 − x 2)0.5 | 点( x , y )は1/4円の円弧上にある |
| y < ( R 2 − x 2)0.5 | 点( x , y )は1/4円の内部にある |
この表で分かる様に、点( x , y )が1/4円の内部にあるか、外部にあるかは、数式により明確に判定できます。
ただ、少し困った事に、点( x , y )は1/4円の内部にあるか外部にあるかの2通りに分類できるのではなく、1/4円の円弧上にぴったり乗っている (つまり、内部と外部の境界上にある) 可能性もあるのです。
次回は、少し細かい話になりますが、点( x , y )が円弧上にぴったり乗っている場合に、この点が1/4円の内部にあると考えるべきか、外部にあると考えるべきかについて説明します。