足し算と引き算だけで円周率の近似値を求めるアルゴリズム(1)

足し算と引き算だけで円周率の近似値を求めるアルゴリズムを考えたので、紹介します。

はじめに

コンピュータを使って円周率の近似値を求める事は、コンピュータの性能の指標として、昔から行われてきました。

円周率を求めるアルゴリズムは色々ありますが、そのどれもが少なくとも四則演算を使いますし、場合によっては、平方根など、もっと複雑な計算が必要な物もあります。

私も中学生の頃に、ライプニッツの公式という簡単な公式で円周率が求まる事を知り、8ビットのBASICが動くパソコン(PC-8001)で円周率を求めるのに夢中になっていた時期があります。ライプニッツの公式は、収束がとても遅い式なのですが、何日もかけて計算して、徐々に円周率に収束していく様子を飽きもせずに見ていました。

ライプニッツの公式は、次の様な公式です。

π = 4 − 4/3 + 4/5 − 4/7 + 4/9 − 4/11 + 4/13 − 4/15 + ・・・

足し算と引き算と割り算だけが出てくる式です。数式は際限なく続くのですが、右の項ほど値が小さくなり、計算を途中で打ち切っても円周率の近似値が出ます。

ライプニッツの公式は、とても簡単な公式なのですが、収束が遅い(多くの項を計算しないとなかなか円周率に近くならない)のと、割り算が出てくるのが欠点です。

コンピュータにある程度詳しい人なら分かると思いますが、四則演算の中で割り算が、他の3つの演算(足し算、引き算、掛け算)と比較すると、圧倒的に時間がかかります。ちなみに、割り算の次には、掛け算が時間がかかります。

先日、その事を考えていた時に、整数の足し算と引き算だけで円周率の近似値を求める方法を思いついたので、報告します。

まずはプログラムの紹介

まずは理屈は抜きに、今回思いついた円周率を求めるアルゴリズムをC++(といっても、C++に固有な機能は使っていないので実質C言語)で実装したプログラムを、次にご紹介します。

#include <stdint.h>
#include <iostream>
#include <cstdio>

int main()
{
  const uint32_t R = 100000000U; // 10憶
  const uint64_t RR = uint64_t(R)*R;
  uint32_t x, y1, y2;
  uint64_t yy1, yy2, nyy, d, s1, s2;

  y1 = y2 = R;
  yy1 = yy2 = d = RR;
  nyy = RR - R - R + 1;
  s1 = s2 = 0;
  for(x = 0; x < R; x++) {
    while(nyy >= d) {
      yy1 = nyy;
      y1--;
      nyy -= y1 + y1 - 1;
    } // while
    s1 += y1;
    d -= x + x + 1;
    while(yy2 > d) {
      yy2 -= y2 + y2 - 1;
      y2--;
    } // while
    s2 += y2;
  } // for x

  printf("max %1.14f\n",(double(s1) + s1 + s1 + s1) / RR);
  printf("min %1.14f\n",(double(s2) + s2 + s2 + s2) / RR);
  printf("ave %1.14f\n",(double(s1) + s1 + s2 + s2) / RR);
  return 0;
}

最初のRRの宣言で掛け算が出てきていますが、これは定数式ですので、プログラム実行時に掛け算が行われるわけではありません。また、Rが1000000000(10億)ですので、R*Rの計算は、BCD( 二進化十進符号 )を用いてアルゴリズムを実装する場合は、RRの値は、1の後に18個0を並べただけです。(2進数ならキリの悪い数になりますが)

最後の方に、s1やs2をdouble型にキャストしていますが、これは値をRRで割るためです。

また、値をRRで割るという操作は、BCDを使った固定小数点演算の場合は、小数点の位置を18桁左に移動させて数を読むという事だけですので、実際の計算は伴いません。

そういう訳で、このアルゴリズムをBCDの固定小数点で実装すると、足し算と引き算しか出てこないのです。

このプログラムを論理回路で実装するとすると、BCDの加算器と減算器しか必要ありませんし、しかも負の数を扱いませんので、簡単な回路で実現できるという特徴があります。

このプログラムをPaiza ioで実行できる様にしたのが次の画面です。

実行すると、次の様な表示が出ます。

max 3.14159269358679
min 3.14159261358680
ave 3.14159265358679

maxというのは、円周率がこの値以下だと、計算により保証された値です。またminというのは、円周率がこの値以上だと、計算により保証された値です。さらにaveは、maxとminの平均値を表しますが、これが円周率の良い推定値になっています。

円周率の本当の値は、3.14159265358979・・・ですから、aveの値を見ると、整数の足し算と引き算だけで円周率が12桁求まった事が分かります。

なお、定数Rは計算の繰り返し回数です。R=1000000000(10億)に設定していまが、Paiza ioの画面内で、この値を変えて実行し直すと、繰り返し回数を変えて、計算をし直す事ができます。

例えばR=10に設定して実行し直すと、ave=3.10が得られます。

円の面積を定積分で求める事による円周率の計算アルゴリズム

今回紹介したプログラムでなぜ円周率が求まるのかを説明するのには、少しページ数が要りますので、今回は、導入部分だけ説明します。

紹介したプログラムで使ったのは、定積分により半径が R ( R は大きな整数)の円の面積を求めて、それより円周率を求める手法です。

直交座標の原点が中心となる半径 R の円は、 x とyを2軸の座標として、次の式で表されます。

x ² + y ² = R ² ・・・ (1)

グラフの第1象限(原点の右上の領域)にだけ注目し、 x ≧0 および y ≧0 として式(1)を変形すると、次の様になります。

y = ( R ²– x ²)^0.5 ・・・ (2)

なお、平方根の記号を書くのはHTMLでは難しかったので、この式では0.5乗として表現しています。

式(2)を0 ≦ x ≦ R の範囲で定積分すれば、半径 R の1/4円の面積になります。

半径 R の円の面積はπ R ²ですから、定積分の結果はπ R ²/4になるはずです。

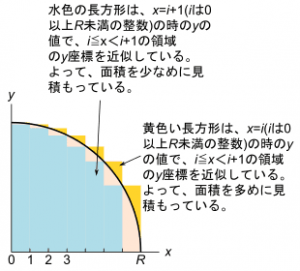
ここで、第1象限の1/4円を0≦ x ＜1、1≦ x ＜2、・・・ R – 1≦x≦ R のR個の領域に分割して、さらに、それぞれの領域を長方形であると近似して、近似的に1/4円の面積を求めてみます。

上の図の水色で表わした長方形は、 x = i + 1( i は0以上R 未満の整数)の時の y の値で、 i ≦ x ＜ i + 1の領域の円周の y 座標を近似しています。よって、水色の長方形の面積を合わせると、ピンク色で表わした実際の円の面積より少し小さくなります。

また黄色で表わした長方形は x = i の時の y の値で、 i ≦ x ＜ i +1の領域の円周の y 座標を近似しています。よって、水色の長方形の面積を合わせると、ピンク色で表わした実際の円の面積より少し大きくなります。

水色または黄色の長方形の面積の合計を求めると、半径 R の1/4円の面積の近似値になります。よって、水色または黄色の長方形の面積の合計を4/ R ²倍すれば、円周率の近似値が求まります。

水色の長方形で円周率の近似値を求めると、必ず実際の円周率より小さな値が求まります。一方で、黄色の長方形で円周率の近似値を求めると、必ず実際の円周率より大きな値が求まります。よって両方の長方形で円周率を近似する事により、「必ず円周率はこの範囲にある」という、範囲を求める事ができます。

加えて言うと、先ほどの図では R =7の場合で作図しましたが、 R を大きな数に設定すると、水色の長方形の面積の合計と、黄色の長方形の面積の合計の比が１に近づきますから、円周率が精度よく求まります。

この様なアイデアで、円周率の近似値を求めるプログラムを組むと、次の様になります。

#include <stdint.h>
#include <iostream>
#include <cstdio>
#include <math.h>

int main()
{
  const uint32_t R = 1000000000U; // 10億
  const uint64_t RR = uint64_t(R)*R;
  uint32_t x;
  double s1,s2;

  s2=0.0;
  for(x = 1; x < R; x++) {
    s2+=sqrt(RR - uint64_t(x) * x);
  }
  s1=s2+R;

  printf("max %1.14f\n",s1*4.0 / RR);
  printf("min %1.14f\n",s2*4.0 / RR);
  printf("ave %1.14f\n",(s1+s2) * 2.0 / RR);
  return 0;
}

このプログラムをPaiza ioで実行できる様にしたのが次の画面です。

実行結果のmaxが、黄色い長方形の面積の合計から求めた円周率の近似値で、minが水色の長方形の面積の合計から求めた円周率の近似値です。またaveは、maxとminの平均値を表しています。

R が大きくなると、(上のプログラムの場合は10億)、円周が非常に細かく分割され、黄色の領域と水色の領域の真ん中をほぼ直線的に円周が突き抜ける事になるので、maxとminの平均値であるaveは、円周率の良い近似値になります。

上のプログラムでは、aveは3.14159265358939と、実際の円周率と13桁一致しています。

ただ、このプログラムには、浮動小数点の演算を行っていたり、掛け算を使っていたり、さらには、計算に時間のかかる平方根を求めていたりと、色々と問題があります。

しかし、このプログラムに少しアイデアを付け足すと、最初に示した整数の足し算と引き算のプログラムに変形できるのです。話が長くなるので、この話は次回にしましょう。