前回は、 x y 平面内の点( x , y )が、半径 R の1/4円(第1象限内)の内部にあるか、外部にあるかを判定するには、 y の値が( R 2+ x 2)0.5より大きいか小さいかを調べればよい事を説明しました。 y の値が( R 2+ x 2)0.5より大きければ、点 ( x , y )は1/4円の外部にありますし、 y の値が( R 2+ x 2)0.5より小さければ、1/4円の内部にあります。
y の値が( R 2+ x 2)0.5とちょうど同じなら、点( x , y )は1/4円の円弧上にあるのですが、今回の記事では、1/4円の面積を求める(つまり円周率を近似計算する)にあたって、ちょうど円弧上にある点をどう扱うべきかを説明します。
また、その説明にあたって、ピタゴラス数という概念が出てきますので、ピタゴラス数についても若干の説明をします。
どうして点が1/4円の内部にあるか外部にあるかを判定する必要があったのか(前回の振り返り)
そもそも、なぜ点( x , y )が1/4円の内部にあるか外部にあるかを判定しなければならないかを振り返ってみましょう。
半径 R の円の面積はπ R 2で求まりますので、半径 R の円の面積を定積分で求めて、 R 2で割れば、円周率πが計算できます。さらに、円の対称性を利用すると、円の面積を求めるには、中心から見て右上の1/4円の面積を求めて、4倍すればいい事が分かります。
中心が x y 座標の原点にある半径 R の円の第1象限における円弧は、次の式を満たします。
y = ( R 2 − x 2)0.5 ・・・ (1)
この式の y の値を0 ≦ x ≦ R の範囲で定積分すれば1/4円の面積が求まりますが、そのまま定積分しようとすると、浮動小数点演算をしなければなりません。
そこで、半径 R が整数の場合について考え、 x 座標および y 座標を、0 ~ R の領域で R 分割し、面積が1の R 2個の正方形のコマに分けて近似計算するのでした。そうすると、1/4円の内部にあるコマの数を数えれば、近似的に1/4円の面積を求める事ができます。
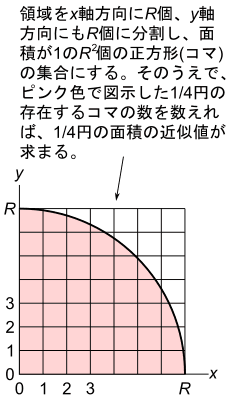
この様に、注目する領域を面積1の正方形のコマに分割すると、1/4円内にあるコマの数も整数ですし、コマの4隅の座標も整数になります。
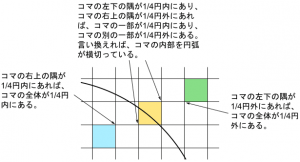
各コマについては、コマ全体が1/4円の外部にある場合と、コマ全体が1/4円の内部にある場合と、コマの一部が1/4円の内部にある場合とがありますが、下の図で分かる様に、コマの右上の隅と、左下の隅が1/4円の内部にあるかどうかを判定すれば、3つのケースのどれにあたるかが分かります。
ここで、点 ( x , y ) において、この点が1/4円の内部にあるか外部にあるかが問題になるわけです。注目している点はコマの右上または左下の隅ですので、 x と y が0以上の整数の場合だけが問題になります。
半径 R の円の円周上に点( x , y )が載る場合を3種類に分類する
あるコマが1/4円の内部にあるか、外部にあるか、それともそのコマの一部だけが内部にあるかを判定する際に、コマの左下の隅または右上の隅が円弧の上にちょうど乗っていた場合は、どう扱えばいいかを考えてみましょう。
x と y が共に0以上の整数の場合に、点( x , y )が原点を中心とする半径 R ( R は自然数)の円の上にちょうど乗るのは、次の3つの場合が考えられます。
- ( x , y ) = (0, R )の場合
- ( x , y ) = ( R ,0)の場合
- x と y と R がピタゴラス数の場合
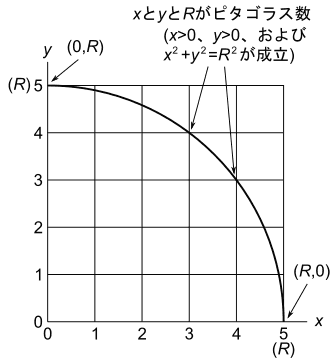
これらの内、1番の( x , y ) = (0, R )の場合と、2番の( x , y ) = ( R ,0)の場合については、点( x , y )が半径 R の円周の上に乗るのは自明です。
また、 点(0, R ) や 点( R ,0)については、コマが1/4円の内部にあるか、外部にあるかを考える場合において、問題になる事はありません。
というのは、今、面積が1の R 2個の正方形のコマに注目しており、それら各々のコマが1/4円の内部にあるか、外部にあるかを判定するには、それぞれのコマの左下および右上の隅が1/4円の内部にあるかどうかを考えればいいからです。
点(0, R )は、問題にしているコマの左上の隅になる事はあっても、左下や右上の隅になる事はありません。また点( R ,0)は、問題にしているコマの右下の隅になる事はあっても、左下や右上の隅になる事はありません。
よって、取り扱いに注意が必要なのは、3番の、 x と y と R がピタゴラス数になる場合だけです。
ピタゴラス数とは
ピタゴラス数とは、直角三角形の3辺の長さになる様な、3つの整数の組の事です。つまり、 x と y と R をそれぞれ自然数として、 x 2 + y 2 = R 2(ピタゴラスの定理)を満たす様な、3つの自然数の組み合わせの事をピタゴラス数と呼びます。
例えば(3,4,5)は、32 + 42 = 52を満たすのでピタゴラス数です。また(5,12,13)も、52 + 122 = 132を満たすのでピタゴラス数です。
余談になりますが、ある3つの自然数の組( x , y , R )がピタゴラス数なら、それぞれの数に共通の2以上の自然数 n を掛けて得られる3つの自然数の組( n x , n y , n R )もピタゴラス数になります。よって、ピタゴラス数は無数にあります。
参考:(3,4,5)がピタゴラス数になっている事を知っていると、それぞれの数を2倍、3倍、4倍、・・・とする事により、(6,8,10)、(9,12,15)、(12,16,20)、・・・と、無数にピタゴラス数を見つける事ができます。
また、3つの整数が互いに素(最大公約数が1)のピタゴラス数を原始ピタゴラス数といいますが、原始ピタゴラス数ですら、無数にある事が分かっています。
参考:(3,4,5)は、3つの数が互いに素なので原始ピタゴラス数です。一方で、(6,8,10)や(9,12,15)や(12,16,20)は、1より大きな公約数を持つので、原始ピタゴラス数ではありません。
この様に、円の半径 R をどんなに大きくしても、円周上にピタゴラス数が含まれる可能性はなくなりませんから、 R が大きな数になっても、コマが1/4円の内部にあるか外部にあるかの判定には、ピタゴラス数の扱いに気を付ける必要があります。
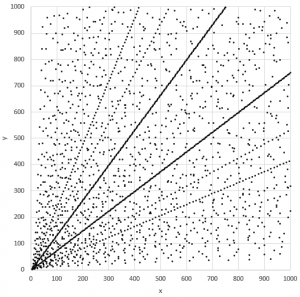
参考:( x , y , R )がピタゴラス数になる組み合わせについて、点( x , y )を x ≦1000、 y ≦1000の範囲で、 x y 平面上にプロットすると、次のグラフの様になります。 R が大きくなるにつれてピタゴラス数の密度が少しずつ減る様子は観察されるものの、結構な密度でピタゴラス数がある事が分かります。
参考:なお、 x と y が共に1000以下のピタゴラス数は、次のC言語のプログラムにより全部計算できます。
ピタゴラス数になる点( x , y )を一律に1/4円の内部だとみなした時に起こる問題
ここで、( x , y , R )がピタゴラス数になる場合に、一律に点( x , y )を半径 R の1/4円の内部だとみなして定積分を行うと、何が起こるか考えてみましょう。
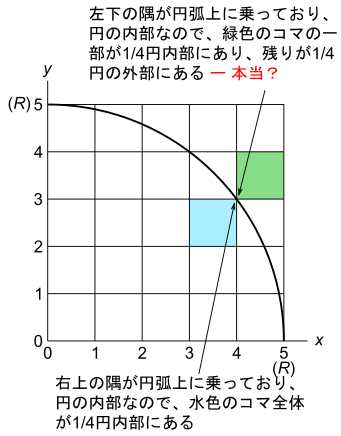
上の図の様に、円弧上の点が右上の隅になる水色のコマと、円弧上の点が左下の隅になる緑色のコマについて考えます。
水色のコマについては、右上の隅が円弧上の点になっており、これは1/4円内部だと考えますので、水色のコマ全体が1/4円内部だと判定されます。
緑色のコマについては、左下の隅が円弧上の点になっています。今、円弧上の点は1/4円の内部だと考える事にしているので、コマの左下の隅が1/4円の内部だという事になってしまいます。
一方で、緑色のコマの右上の隅は、明らかに1/4円の外部です。よって、緑色のコマは、その一部が1/4円の内部で、別の一部が1/4円の外部だと判定されてしまいます。
この判定は妥当でしょうか?図を見ると、緑色のコマ全体が1/4円の外部にある様に見えますよね?
コマの左下の隅の点を、コマを構成する点だと考え、円弧上の点を1/4円を構成する点だと考えると、確かに緑色のコマは、一部が1/4円内にあり、別の一部が1/4円外にある事になります。コマの左下の隅の一点が、緑色のコマと1/4円とで共有されているからです。
ただし、共有されている部分はたった1点です。1点の領域の面積は0です。緑色のコマの、左下の隅の1点を除く部分の面積は、1となります。
よって、緑色のコマの、1/4円外のにある部分の面積に興味がある場合は、緑色のコマの一部が1/4円内にあると考えるより、緑色のコマ全部が1/4円外にあると考える方が妥当なのです。
この様に、円弧上の点を円の内部だと考えると、円弧に外接するコマ(緑色のコマ)の一部が1/4円内にあると判定してしまって、積極的な手法で1/4円の面積を見積もる際に、面積を過剰に評価するという問題が発生します。
ピタゴラス数になる点( x , y )を一律に1/4円の外部だとみなした時に起こる問題
それでは次に、( x , y , R )がピタゴラス数になる場合に、一律に点( x , y )を半径 R の1/4円の外部だとみなして定積分を行うと、何が起こるか考えてみましょう。
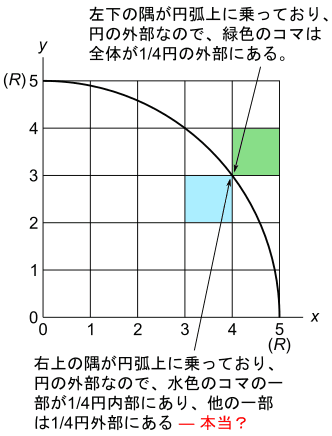
円弧上の点を1/4円の外部だとみなす場合は、左下の隅が円弧上に乗る緑色のコマでは、問題が発生しません。緑色のコマの左下の隅は、1/4円の外部なので、緑色のコマ全体が1/4円の外部だと判定されます。
一方で、右上の隅が円弧上に乗る水色のコマでは、問題が発生する様になります。右上の隅が1/4円の外部で、左下の隅は明らかに1/4円の内部なので、個のコマは、一部が1/4円の内部で、別の一部が1/4円の外部という事になってしまいます。
この場合も、水色のコマで1/4円の外部になるのは、コマの右上の隅のたった1点なのですから、面積を問題にする場合は、水色のコマ全体が1/4円の内部にあると考えて計算すべきです。そうしないと、消極的な手法で1/4円の面積を見積もる場合に、面積を過少に評価します。
コマの右上の点か左下の点かで円弧上の点の扱い方を変えればいい
結局、円弧上の点を、一律に1/4円の内部とか、外部とかと判定せずに、コマの左下の点の場合は1/4円の外部と判定し、右下の点の場合は1/4円の内部と判定すれば、うまく1/4円の面積を見積もる事ができます。
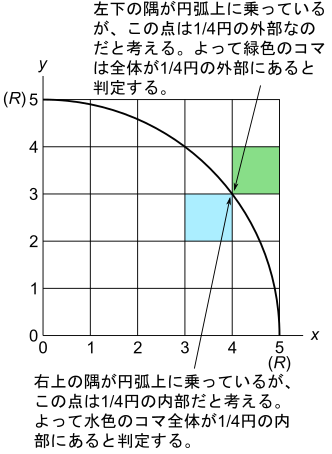
今回話した事をまとめると、点( x , y )が式(1)を満たす場合(円弧上の点の場合)は、コマの左下の隅の場合は1/4円の外部だと考え、コマの右上の隅の場合は1/4の内部だと考えて、1/4円の面積を見積もると、面積の上限を過剰に見積もったり、面積の下限を過少に見積もったりする問題は避けられるという事になります。
次回は、いよいよ整数演算だけで円周率の近似値を求めるプログラムを作ります。