ピカピカ光るクリスマスツリーおばけの製作(6)

4-5-4.duty変数の変化

前のページの後半ではtick変数とcnt変数の変化について考えましたが、次にduty変数について考えて見ましょう。

duty変数はstatic宣言されていませんので、loop関数を抜けると消滅してしまいます。もう一度loop関数が呼ばれたときには、以前の値を保持している保証がないことに注意してください。

duty変数は、loop関数の中で、2回値をセットされます。1回目にセットされる値と2回目にセットされる値では、意味が違うので、本来は別の変数を使う方がいいのかも知れませんが、メモリの節約の意味で一つの変数を使いまわしています。

duty変数に値をセットする1番目の場所を抜き出すと、次の様になります。

  if(cnt>TickNum) {
    duty=TickNum*2-cnt;
  } else {
    duty=cnt;
  } // if

このコードを見て分かるように、duty変数はcnt変数から求めています。

cnt変数が8より大きければ、16からcnt変数の値を引いた結果をduty変数に代入し、cnt変数が8以下ならば、cnt変数そのものをduty変数に代入しています。(定数TickNumは8であることに注意) その結果、cnt変数が0→1→2→3→4→5→6→7→8→9→10→11→12→13→14→15と変化すると、duty変数はそれに応じて0→1→2→3→4→5→6→7→8→7→6→5→4→3→2→1と変化します。ただし、赤色で書いた数字は、if文の条件式cnt>TickNumが成立してduty=TickNum-2-cnt;より求められた値を表わしており、黒色で書いた数字は、if文の条件式が成立せずにduty=cnt;より求められた値を表わしています。

次に、duty変数に値をセットする2番目の場所を抜き出すと、次の様になります。

  duty=(cnt+TickNum/2)%(TickNum*2);
  if(duty>TickNum) duty=TickNum*2-duty;

1行目のduty=(cnt+TickNum/2)%(TickNum*2);は、cnt変数に4を足した上で16で割り、その剰余(あまり)をduty変数に代入しています。その結果、cnt変数が0→1→2→3→4→5→6→7→8→9→10→11→12→13→14→15と変化すると、duty変数はそれに応じて4→5→6→7→8→9→10→11→12→13→14→15→0→1→2→3と変化します。

さらに2行目のif(duty>TickNum) duty=TickNum*2-duty;は、duty変数が8より大きくなると、16からduty変数を引いた答えでduty変数を更新します。最終的に、cnt変数が0→1→(中略)→14→15と変化すると、duty変数はそれに応じて4→5→6→7→8→7→6→5→4→3→2→1→0→1→2→3と変化します。ここで、赤色で書いた数字は、if文の条件が成立することにより、更新された数字を意味します。

分かりやすいように、cnt変数の値とduty変数の値の関係を表にすると、表4の様になります。duty変数はloop関数内の2箇所で値をセットされますが、1箇所目と2箇所目でセットされる値を、それぞれduty変数(前半)およびduty変数(後半)と呼んで区別しています。

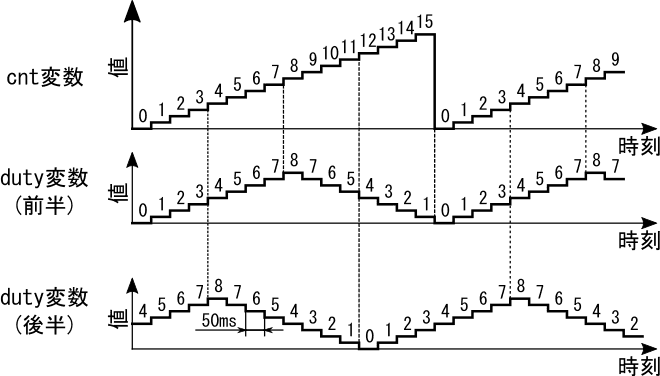
表4をグラフにすると、図10の様になります。

図10、CNT変数とduty変数(前半・後半)の値の関係

duty(前半)とduty(後半)は、共に800[ms]周期の三角波となっており、duty(後半)はduty(前半)に比べて位相が90度進んでいる事が、このグラフより分かります。

この後説明するとおり、実はduty(前半)は、D2の信号線で制御されるLED_CとLED_Gの明るさを表わす変数です。またduty(後半)は、D3の信号線で制御されるLED_DとLED_Hの明るさを表わす変数です。つまり、LEDにより明るさの変化に位相差をつけるために、これまで説明してきたようなduty変数の計算を行っていたのです。

4-5-5.D0～D3のPWM制御

ここで、スケッチの中で、D0およびD2の信号線に対して出力を行っている部分に注目しましょう。

  digitalWrite(0,tick>=duty ? HIGH : LOW);
  digitalWrite(2,tick< duty ? HIGH : LOW);

これら2つのdigitalWrite関数で、D0とD2の信号線の論理レベル(LかHか)を決めています。これらのdigitalWrite関数が実行される時点では、duty変数は表4および図10の、duty変数(前半)の値を取ります。

D0は、tick変数の値がduty変数(前半)の値以上であればH、そうでなければLになります。一方でD1は、tick変数の値がduty変数(前半)の値より小さければH、そうでなければLになります。

duty変数(前半)の値が50[ms]ごとにしか更新されないのに対して、tick変数はloop関数が呼ばれるたびに値が更新されます。そのため、duty変数(前半)の値が1回更新される間に、tick変数はかなりの回数更新される事になります。

変数値の更新頻度の違いに注意して、duty変数(前半)およびtick変数の値と、D0およびD2の論理レベルの関係をグラフにすると、図11の様になります。

図11、duty変数(前半)、tick変数、D0、D2の関係

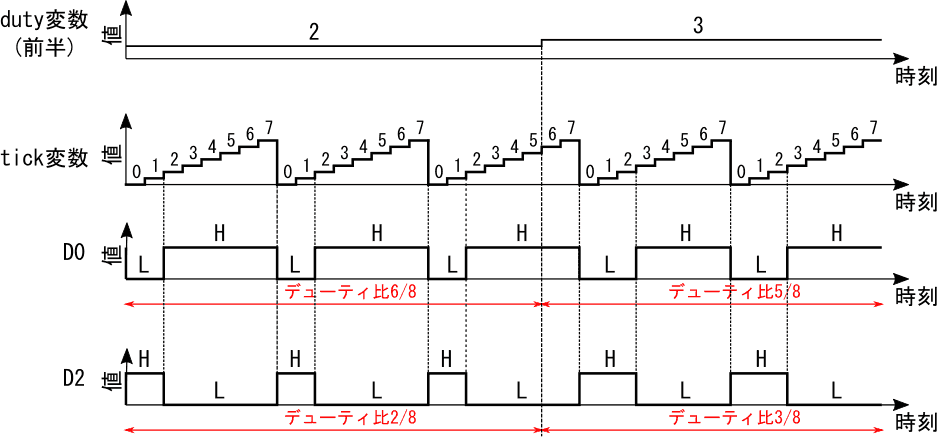
この図からわかるように、D0のデューティ比は1-duty(前半)/8に、D2のデューティ比はduty(前半)/8になります。

また次に、D1およびD3の信号線に対して出力を行っている部分に注目しましょう。

  digitalWrite(1,tick>=duty ? HIGH : LOW);
  digitalWrite(3,tick< duty ? HIGH : LOW);

これら2つのdigitalWrite関数実行時では、duty変数はduty変数(後半)の値を取ります。

D0およびD2のデューティ比を求めた際と同様の考察により、D1のデューティ比は1-duty(後半)/8に、D3のデューティ比はduty(後半)/8になる事が分かります。

以上の議論を踏まえて、cnt変数の値、duty変数(前半・後半)の値、およびD0～D3の信号のデューティ比の関係をグラフにすると、図12の様になります。

図12、cnt変数の値、duty変数(前半・後半)の値、およびD0～D3の信号のデューティ比の関係

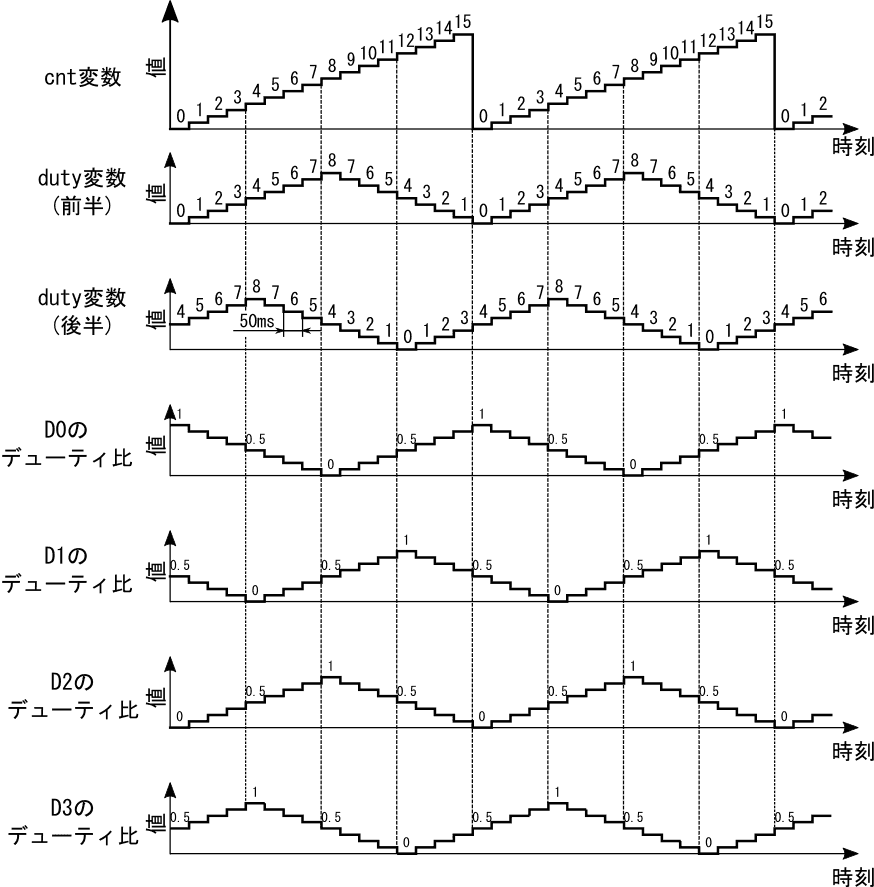
この図より、D0～D3のデューティ比は全て三角波になっており、D1、D2、D3、はD0に対して、それぞれ90度、180度、270度位相が進んでいるのがわかります。D0～D3の信号線は、3ページの表2に示した様に、それぞれが2つずつのLEDを制御しています。よって、8個のLEDは、明るさの変化の位相が90度ずつずれた4つのグループから構成される事が分かります。

4-5-6.D0～D3の信号波形の測定

CN2にLAP-C(16064)というロジックアナライザを接続し、D0～D3の信号波形を測定をしました。測定風景を写真36に示します。

なお、ロジックアナライザについては、Arduino用ヘッダシールドの製作(2)の記事に説明が載っていますので参考にしてください。

↑ 画像をクリックすると拡大

写真36、信号波形の測定風景

D0信号の、デューティ比が1から0へ減少する部分のD0～D3の観測波形を、図13に示します。

↑ 画像をクリックすると拡大

図13、D0～D3の観測波形(半周期)

D0信号のデューティ比が1→0.5→0と減少していく過程で、D1信号のデューティ比は0.5→0→0.5、D2信号のデューティ比は0→0.5→1、D3信号のデューティ比は0.5→1→0.5と変化しています。これらの変化は、図12のグラフの左端の部分と一致しています。

また、D0信号のデューティ比が1になってから0になるまでの半周期の時間を計測すると、389[ms]となり、理論的に予測される400[ms]とほぼ一致しています。

次に、D0 信号のデューティ比が1から7/8に変わる付近の拡大波形を図14に示します。

↑ 画像をクリックすると拡大

図14、D0～D3の観測波形(拡大)

D0信号のデューティ比が1から7/8に変わって最初のPWM信号の周期の部分に注目すると、Lになっている時間が555[μs](=0.555[ms])、Hになっている時間が3.895[ms]となっています。

これらの測定結果より、PWM信号の周期を求めると、0.555+3.895=4.450[ms]となります。またPWM信号の周波数は、その逆数から求まり、1000÷4.450≒225[Hz]となります。前のページで説明したとおり、LEDの点滅がおおむね30～50Hz以上の速さになると、人の目には点滅が感じられなくなり、デューティ比に応じた平均的な明るさを感じる様になります。このLED制御基板では224Hzで点滅を行うので、点滅の弁別能力の個人差を考慮しても、人間には点滅が感じられないだけの点滅周波数を実現している事が分かります。

また、デューティ比は3.895÷4.450≒0.8753となり、理論値の0.875とほぼ等しくなっています。

4-5-7.正確なデューティ比を得るために必要な工夫

タイマを用いてハードウェア的にPWM信号を発生する場合は、タイマのレジスタに、必要なデューティ比を得るための設定を行えば、タイマが自動的に正確なデューティ比のPWM信号を発生してくれます。しかしながら、今回の様に、純粋にソフトウェア的にPWM信号を発生する場合、正確なデューティ比を得るには、ある工夫が必要です。

もう一度PWM調光版のスケッチのloop関数を見てください。

void loop() {
  static byte tick=0;
  static byte cnt=0;
  byte duty;

  digitalWrite(4,cnt==0 ? HIGH : LOW);

  if(cnt>TickNum) {
    duty=TickNum*2-cnt;
  } else {
    duty=cnt;
  } // if

  digitalWrite(0,tick>=duty ? HIGH : LOW);
  digitalWrite(2,tick< duty ? HIGH : LOW);

  duty=(cnt+TickNum/2)%(TickNum*2);
  if(duty>TickNum) duty=TickNum*2-duty;

  digitalWrite(1,tick>=duty ? HIGH : LOW);
  digitalWrite(3,tick< duty ? HIGH : LOW);

  tick=(tick+1)%TickNum;

  if(millis()-StartTime>interval) {
    StartTime+=interval;
    cnt=(cnt+1)%(TickNum*2);
  } // if
} // loop

loop関数の中には、if文の条件により、実行される場合と実行されない場合がある命令が含まれます。つまり、条件によりloop関数の実行時間が速くなったり遅くなったりします。

loop関数の実行時間がばらつくと、PWM信号の周期やデューティ比もばらつく原因となりますので、loop関数(の各部分)は、どの様な条件で実行されても、同じ時間で実行されるように作る必要があります。処理時間の長い命令を含む行は、特に実行時間をそろえる必要があります。

loop関数では、digitalWriteとmillisの2種類の関数を呼び出していますが、関数の呼び出しは、スタックの操作を伴うため、時間がかかります。よって、条件によって関数を呼び出したり呼び出さなかったりというコーディングは避けるべきです。

例えば

  digitalWrite(0,tick>=duty ? HIGH : LOW);
  digitalWrite(2,tick< duty ? HIGH : LOW);

の2行は、loop関数の呼び出しの度にtick変数の値が0→1→2→3→4→5→6→7→0→1→…と変化する事に注目して、出力端子の真理値が変化する時にだけdigitalWrite関数を呼び出すようにすれば、

  if(tick==duty) {
    digitalWrite(0,HIGH);
    digitalWrite(2,LOW );
  } else if(tick==0) {
    digitalWrite(0,LOW );
    digitalWrite(2,HIGH);
  }

と書き換えられます。処理時間のばらつきが問題にならないプログラムなら、元のコードと同じ結果が得られるはずです。

しかしながら、ソフトウェアでPWM信号を発生するプログラムでは、tick==dutyもtick==0も成立しない場合にdigitalWrite関数が呼び出されず、実行時間が短くなる事が問題となります。

また

  tick=(tick+1)%TickNum;

も、

  tick++;
  if(tick==TickNum) tick=0;

と書く方が直感的な書き方となります。しかしtick==TickNumが成立するかどうかでtick=0;が実行されたりされなかったりするという意味では、あまり良くない書き方になります。ただし、tick=0;には関数呼び出しが含まれず、極めて短時間で実行されるため、先のdigitalWrite関数の場合よりは、弊害が少ないといえます。

現状のloop関数では、例えばif(duty>TickNum) duty=TickNum*2-duty;など、条件によって実行されたり実行されなかったりする命令が一部残っていますが、実行時間の短いものはあえて放置してあります。

これを例えば

  if(duty>TickNum) {
    duty=TickNum*2-duty;
  } else {
    duty=duty;
  }

などと書き換え、duty>TickNumが成立しない場合にダミーの代入文(duty=duty;)を実行して、なるべく実行時間をそろえようとしても、コンパイラの最適化により、結局if(duty>TickNum) duty=TickNum*2-duty;と同様のコンパイル結果になったりします。(強いていうなら、dumy変数をvolatile宣言すれば、この手の最適化は回避できますが)

アセンブラでプログラムを組む場合なら、nop命令で実行時間を調整するなどして、どの条件でも完全に実行時間が同じになるように調整できますが、CやC++などの高級言語を使う場合は、完全な調整はまず無理でしょう。

PWM信号の周波数が下がっていいなら、loop関数の最初か最後でdelayMicroseconds関数を呼び出すなり、空ループを回すなりして時間を稼ぎ、条件的に実行される命令の実行時間がloop関数全体の実行時間に占める割合を、低下させる方法もあります。ただし、空ループを使う場合は、ループ変数をvolatile宣言するなりして、空ループがコンパイラの最適化により削除されないように、工夫が必要です。

4-5-8.D4信号の波形について

D4信号については、digitalWrite(4,cnt==0 ? HIGH : LOW);により、cnt変数が0の場合だけHになる様にしています。(つまり、全体の1/16の時間だけHになる)

D4信号はLED制御基板上のLED1を制御しています。このLED1は、基板に電池が接続されており、回路が動作している事を確認するためのLEDです。電源接続時は常にLED1を点灯するようにしても良かったのですが、常時点灯していると、マイコンのプログラムが暴走していてもそれをLEDの点灯状態から判断できないのと、LEDが消費する平均電力が大きくなるのとの2つの理由で、点滅させるようにしています。

5.電池の寿命に関する考察

電池で動作する機器を設計する場合、電池の寿命が何時間くらいになるかを見積もる事が重要となります。便利な装置を設計しても、頻繁に電池交換が必要になるのなら、魅力は半減してしまいます。そこで、今回設計したクリスマスツリーのイルミネーション用LED制御基板をPWM調光版のスケッチで動作させた場合について、電池寿命を大雑把に計算してみましょう。

今回は、ATtiny85を制御用マイコンに使いましたが、データシートによると、クロック4[MHz]、電源電圧3[V]の場合の消費電流は典型値で1.5[mA]、最大値で2.5[mA]となります。電源電圧が一定なら、消費電流はおおむねクロック周波数に比例します。(クロック周波数を極端に低くした場合を除く) よって、今回1[MHz]のクロックで動作させている事から、1.5÷4≒0.38[mA]程度の消費電流になる事が期待されます。しかしながら、1[mA]未満の消費電流は、LEDの消費電流に比べて低く、ほぼ無視する事ができます。

今回の回路では、クリスマスツリーの装飾用として、8個のLED(LED_A～LED_H)を使っています。また、基板の動作確認用のLEDを1個(LED1)使っています。

これらのLEDは、全て160[Ω]の抵抗を介して、マイコンのGPIOピンに接続されています。GPIOピンの内部抵抗が、160[Ω]に対して十分低いという仮定をすると、GPIOピンがHの時に、電源電圧と同じ3Vが160[Ω]とLEDの直列回路に印加されます。(実際にはGPIOピンの内部抵抗のために、3Vより若干低い電圧になる)

赤色LEDの順方向電圧(VF)は、LEDの型番や順方向電流(IF)により若干変わるものの、おおむね2[V]程度と考えられます。よって、GPIOピンがHを出力している際にLED1個に流れる電流は、(3-2)÷160≒0.0063=6.3[mA]となります。

クリスマスツリーの装飾用のLEDは、0～1の範囲で、PWM信号のデューティ比が時間的に変化しますが、長時間で平均を取ると、平均デューティ比は0.5となります。装飾用LEDは全部で8個あるので、これら全ての平均消費電流は6.3×0.5×8=25.2[mA]となります。

また、動作確認用のLED1は、デューティ比1/16(周期0.8[s])の信号で駆動されます。よって平均消費電流は6.3×(1/16)≒0.4[mA]となります。

以上より、9個全てのLEDの平均消費電流は、25.2+0.4=25.6[mA]となります。

Wikipediaの乾電池の項目には、単3アルカリ乾電池の容量の目安として、2000～2700[mAh]という数字が載っています。容量を低めに見積もって2000[mAh]とし、マイコンの消費電流を無視してLEDの消費電流のみから電池の寿命を計算すると、2000÷25.6≒78.1[時間]≒3.3[日]となります。(電圧1.5[V]で容量が2000[mAh]の電池を2個直列に接続すると、3[V]、2000[mAh]になることに注意。直列接続の場合は、複数個電池をつないでも、mAhの単位で表わした容量は増えない)

新品の電池を使えば、3日間連続使用できるのですから、クリスマスパーティーのあと、サンタさんがプレゼントを持って来てくれるのを歓迎するために、靴下のそばで一晩中クリスマスツリーのイルミネーションを光らせたとしても、朝まで余裕で電池が持つ計算になります。

このページで使われている用語の解説

• digitalWrite関数
• GPIO
• PWM
• スケッチ
• デューティ比
• 抵抗
• 真理値

関連ページ

• Arduino用ブートローダ/スケッチライタの製作
  ATtiny85にArduinoのスケッチを書き込める装置。
• Arduinoで作った回路の小型化(Arduino互換機の製作)
  Arduino互換機を自作して回路を小型化・低コスト化。
• ArudinoでグラフィックLCDを動かす(SG12864ASLB-GB編)
  PWM制御で液晶モジュールのコントラスト調整をした例。
• 単3ニッケル水素電池充電器の製作(7)
  電圧をPWM制御する電源回路の話。
• Arduino用ヘッダシールドの製作(3)
  Arduinoの信号を取り出してロジックアナライザなどで観察するためのヘッダシールドの話。
• Arduino starter kit with Logic Analyzerの紹介と解説(1)
  Arduinoとロジアナの入門キットの解説。

関連製品

	商品名	Arduino用ブートローダ/スケッチライタキット
	税抜き小売価格	3000円
	販売店	スイッチサイエンス
	サポートページ	Arduino用ブートローダ/スケッチライタキットサポートページ

このサイトの記事が本になりました

書名：Arduino 電子工作

ISBN:978-4-7775-1941-5

→工学社の書籍の内容の紹介ページ

本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。

このサイトの中の人が書いた本です。

書名：電子工作で学ぶ論理回路入門

ISBN:978-4-7775-2280-4

→工学社の書籍の内容の紹介ページ

→この本の紹介記事

本のカバーの写真か書名をクリックすると、Amazonの書籍購入ページに移動します。