↑ 画像をクリックすると拡大
図3(再掲)、リレーの原理図
| 2020年06月06日 | 公開。 |
論理回路を作る場合に限らず、リレーを使う場合は、リレーのコイル電流を外部のスイッチで遮断する際に、コイルの両端にサージ電圧と呼ばれる短時間の高電圧が発生します。このサージ電圧に対して適切な対策をしないと、回路が壊れたり、寿命が短くなる原因になります。この項では、リレーのコイルにサージ電圧が発生する仕組みついて解説します。
参考:この項は、NOT回路の動作に本質的にかかわる事を説明している訳ではありませんので、余裕のある人や、リレーのコイルのアナログ回路的な振舞いに興味のある人だけ読んでください。この項には少し難しい数式が多く出てきますが、これらの数式が理解できなくても、リレーを使った回路の設計はできます。
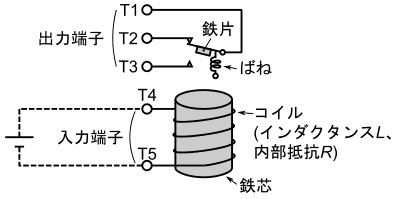
ここでリレーの動作原理を振り返ってみましょう。図3はリレーの原理図です。
リレーは、入力端子からコイルに電圧を掛けたり掛けなかったりして、コイルと鉄芯からなる電磁石に磁界を発生させたり発生させなかったりする事で、スイッチを切り替える部品でした。
ここで今注目したいのは、コイルにはインダクタンスがあり、自己誘導を起こす事です。
参考:自己誘導とは、コイルに流れる電流が変化する事で、コイルに発生する磁束が変化し、その磁束の変化により電磁誘導が起こり、コイル自身に誘導起電力が発生する現象を指します。
コイルに掛かる電圧を0Vと電源電圧Eの間で切り替えたい場合、図19の様に、電源とリレーのコイルの間にスイッチSW1を設ける場合が多くあります。
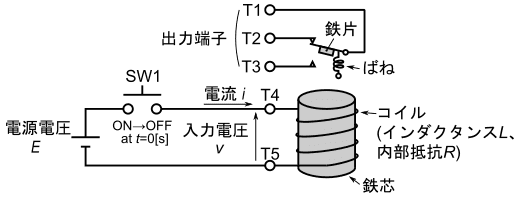
SW1はプッシュスイッチの記号を使っていますが、
Deprecated: strlen(): Passing null to parameter #1 ($string) of type string is deprecated in /home/synapse-hard/synapse.kyoto/public_html/common.php on line 2270
Deprecated: strlen(): Passing null to parameter #1 ($string) of type string is deprecated in /home/synapse-hard/synapse.kyoto/public_html/common.php on line 2270
Deprecated: strlen(): Passing null to parameter #1 ($string) of type string is deprecated in /home/synapse-hard/synapse.kyoto/public_html/common.php on line 2270
heref="https://www.nkkswitches.co.jp/support/klg/knowledge.html>トグルスイッチや、半導体スイッチ(MOS-FETなど)、リレーのスイッチ部など、どんな種類のスイッチでも構いません。
この図では、電源の+極とリレーのT4端子の間にスイッチが入っていますが、電源の−極とリレーのT5端子の間にスイッチが入っている場合でも、この後説明するサージ発生の仕組みは変わりません。
この様な、SW1のON・OFFの切り替えでコイルへの入力電圧を制御する回路において、スイッチがONからOFFに切り替わった瞬間(およびその直後)に何が起こるか考えてみましょう。
大雑把な話をすると、コイルに流れる電流を変化させると、その電流の変化を阻止する方向に、コイルの両端に自己誘導起電力が発生します。その結果として、図19のT4が−側、T5が+側の高い電圧が、スイッチをOFFした瞬間に発生します。この様な、短時間の高電圧をサージ電圧といいます。
注:コイルで発生するものでなくても、短時間に発生する高電圧、大電流であればサージと呼びます。(短時間の高電圧はサージ電圧で、短時間の大電流はサージ電流) コイルの電流を遮断するのとは異なる仕組みで発生するサージには、例えば落雷に伴って発生する雷サージが挙げられます。
図20にコイルの両端電圧vの波形の概略図を示しますが、時刻t=0において、負の極性のサージ電圧が発生している事が分かります。
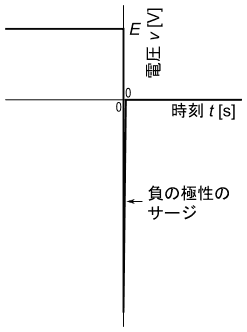
t<0の領域では、スイッチがONになっており、電源電圧Eがコイルの両端にそのまま掛かるので、v=Eとなります。
tがある程度0より大きい領域では、スイッチがOFFになっている事により、コイルに流れる電流iが0で一定になっており、その結果v=0となります。
時刻t=0(とその直後短時間)においては、コイルに流れる電流iが急減するため、その電流変化を阻止する方向に、コイルの両端に高い自己誘電起電力が発生します。この時に発生する様な、短時間の高電圧の事をサージといいます。
リレーのコイルで発生するサージ電圧を放置すると、リレー自身や周囲の部品に高電圧がかかるため、それらの部品が破損したり、それらの部品の寿命が短くなったりする原因になります。そのため、何らかの対策が必要ですが、2ページの図5のダイオードD1が、このサージを防止するための部品です。ダイオードがリレーのコイルで発生するサージ電圧を防止する仕組みについては、次項で説明します。
参考:図19の様に、コイルの電流をスイッチで遮断する事により発生するサージ電圧が、引き起こす可能性が高い不具合としては、スイッチの接点付近の空気の絶縁破壊が挙げられます。スイッチがOFFになる瞬間には、接点同士が接触している状態から、徐々に離れていきます。接点同士が離れた瞬間に電流が遮断され、コイルにサージが発生しますが、その高電圧で接点間の空気が絶縁破壊します。空気は1mm当たり約3000Vまでの電圧に耐えられますが、それ以上の電圧がかかると絶縁性が失われ、放電が起こります。スイッチがOFFになった直後は、サージが発生している上に、接点間の距離が非常に近いので、容易に接点間の空気が絶縁破壊します。空気が絶縁破壊して火花が飛ぶ(火花放電する)事で、接点が欠けたり、接点同士が融着する(つまりスイッチがOFFにならなくなる)事があります。
リレーのコイルでサージが発生するの仕組みを数式で議論するために、各種変数や定数を定義しておきます。
リレーのコイルを駆動するための電源の電圧をE[V]とします。また、コイルのインダクタンスをL[H]、内部抵抗(巻き線抵抗)をR[Ω]とします。
注意:電源の内部抵抗や配線の抵抗、およびスイッチS1の接点の接触抵抗は、コイルの内部抵抗Rよりも十分に小さく、無視できるものとして議論します。また、コイルのインダクタンスは厳密には一定値ではなく、リレー内部のスイッチの状態によってわずかに変わりますが、ここではインダクタンスが一定だとして議論します。スイッチの状態によってインダクタンスがわずかに変わるのは、鉄片がコイルに引き付けられると、磁路の磁気抵抗がわずかに減少するためです。
この時、コイルにながれる電流i[A]とコイルの両端電圧v[V]の時間的な変化を考えてみましょう。なお、時刻はt[s]とし、スイッチがONからOFFに切り替わった時点をt=0[s]とします。
リレーのコイルは、図21に示す様な、インダクタンスがL[H]で内部抵抗がない理想的なコイルと、R[Ω]の抵抗が直列につながった等価回路を使って、その特性を解析できます。
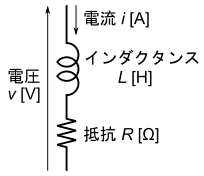
リレーのコイルを分解すると、この図の様にインダクタンスがL[H]で内部抵抗がない理想的なコイルと、R[Ω]の抵抗に分かれて出てくるという訳では、もちろんありません。インダクタンスや抵抗は、コイルの巻き線全体にわたって、分布しています。
この等価回路は、内部抵抗がない理想のコイルと抵抗の直列回路を用いて電圧vと電流iの関係を解析しても、実際のリレーのコイルのvとiの関係と、全く同じ関係が得られる事を表しています。
この等価回路において、電圧vと電流iの関係は、式(2)の様に表されます。
ここで、スイッチがONの期間とOFFの期間に分けて、現象を解析します。
まず、スイッチがONの期間、すなわちt<0の期間に起こる現象について考えます。
t<0においては、スイッチがONなので、コイルには電源電圧Eがそのままかかります。つまり、式(3)が成立します。
また電流iに関しては、直流の電源を用いており、かつt<0の期間はスイッチがONのまま変化がない訳ですから、過渡現象は起こらず、コイルには直流電流が流れるはずです。すなわち、式(4)が成立します。
式(2)に式(3)と式(4)を代入すると、式(5)が得られます。
次に、スイッチがONになってから、すなわちt≧0の期間の現象について考えます。
スイッチSW1が時刻t=0においてOFFになると、それ以降は電流iが流れるルートが絶たれてしまうので、式(6)が成立します。
式(5)と式(6)から電流iの時間変化をグラフに表すと、図22の様になります。
この図に示す波形のiを式(2)に代入する事により、vの波形を求めます。
t<0の範囲では、式(5)の両辺をtで微分する事により、式(7)が得られます。
注:式(7)は、式(4)と同じ式です。
この式(7)と式(5)とを式(2)に代入する事により、t<0におけるvは式(8)の様に求まります。
注:式(8)は、式(3)と同じ式です。
一方でt>0の範囲では式(6)よりi=0が成立しますから、両辺をtで微分する事により、式(9)が得られます。
この式(9)とi=0とを式(2)に代入する事により、t>0におけるvは式(10)の様に求まります。
この様にt<0とt>0の範囲では電圧vが0になる事が分かりましたが、問題は、t=0におけるvの値がいくらになるかです。
実は、t=0においては、vの値が求まりません。というのは、t=0においては、iがERから0に跳躍的に(不連続に)変化しているからです。そのため、t=0ではiをtで微分できないのです。didtが求まらければ、式(2)からvを求める事はできません。
参考:関数がある点で連続である事は、その関数がその点において微分可能であるための必要条件です。(しかし、十分条件ではありません。)
図22に示す様に、t=0においてiの波形が不連続になるため、iがtで微分できないのが、vが求まらない原因なので、ここで、図22に近い形で、かつ全範囲でiがtで微分できる、図23の様な波形を考え、近似的な解を求める事を考えます。
図23において、t0は正の定数です。
図23の波形は、t<−t0、−t0≦t≦t0、およびt>t0の3つの領域に分けて、式(11)～式(13)の様に定義されます。
式(5)と式(11)とを比較すると、図22と図23の波形は、t<−t0の領域で一致している事が分かります。
同様に、式(6)と式(13)とを比較すると、図22と図23の波形は、t>t0の領域でも一致している事が分かります。
一方で、−t0≦t≦t0の領域では、図22と図23の波形は一致しません。
図22の波形では、時刻t=0においてiの値がERから0に、不連続に変化しています。
図23の波形では、時刻tが−t0からt0に進むにしたがって、電流iの値がERから0まで、連続かつなめらかに減少します。
注:ここでなめらかという言葉は、一階微分可能という意味で使っています。
この様に、図22と図23の波形は異なる物ですが、定数t0をだんだん小さくして0に漸近させると、式(11)～式(13)で定義される図22の波形は、図23の波形に近くなってきます。(図24参照)
図23の波形でt0→0の極限を考えると図22の階段状の波形が得られる事を分かった上で、図22の波形を定義する式(11)～式(13)をt微分してみましょう。
式(11)～式(13)をtで微分すると、それぞれ式(14)～式(16)が得られます。
式(14)～式(16)からdidtの時間変化のグラフを作図すると、図25の様になります。
このグラフを見ると分かる様に、t<−t0とt>t0の領域ではdidt=0となります。
また、−t0≦t≦t0の領域ではdidtは負の値になりますが、時刻t=0において最小値−Eπ4Rt0を取ります。
ここでt0の値を小さくして0に漸近させる事を念頭に、定数t0の値を変えてdidtの波形を描くと、図26の様になります。
この様に定数t0を小さくして0に近づけるほど、didtが負の値になる時間の幅(2t0)が狭くなり、最小値(−Eπ4Rt0)がより小さくなります。
この時に、図27に示す様に、横軸とdidtが囲む面積は、t0の値に関わらず、ERで一定になる事に注意が必要です。
これを数式で表すと式(17)になります。
この式が成立するのは、didiをtで積分するとiになる事と、時刻−t0から時刻t0までの間にiが−ER増加する(ER減少する)事によります。
参考:式(15)を−t0からt0までtで定積分しても、式(17)を証明できます。詳しくは後述のコラムをご覧ください。
図24においてt0を0に漸近させると、電流iの波形が、実際にコイルに流れる電流の波形(図22)に収束するのでしたが、この時、図27のdidtの波形は、次の性質を持つ波形に収束します。(図28参照)
di/dtは、後述するインパルス関数になります。
ところで、変数tの関数f(t)が次の3つの性質を満たすとき、その関数f(t)をインパルス関数(衝撃関数)といいます。
インパルス関数をグラフに表すと、図29の様になります。
インパルス関数は、t≠0の場合はf(t)=0となるので、グラフに描けますが、t=timpにおいてはf(timp)=∞またはf(timp)=−∞となるため、有限の大きさのグラフに正確に描く事ができません。そこで、∞あるいは−∞の値を描く代わりに、上矢印(∞の場合)または下矢印(−∞の場合)で表す習慣があります。この際、矢印の長さは、Cの絶対値となる様に描きます。
図28から分かる様に、リレーのコイル電流iの時間微分didtはインパルス関数になります。
インパルス関数において、特にC=1の場合を単位インパルス関数といいます。(図30参照)
さらに、単位インパルス関数において、特にtimp=0の場合をデルタ関数といい、δ(t)と表します。(図31参照)
デルタ関数δ(t)は、次の3つの性質を満たします。
なお、デルタ関数を使えば、図30の単位インパルス関数はδ(t-timp)と表現でき、図29のインパルス関数は、Cδ(t-timp)と表現できます。
注:デルタ関数には「関数」という名前が付いていますが、δ(0)=∞である時点で、関数の概念から外れています。仮にt=0を定義域から外せば関数にはなりますが、今度は∞−∞δ(t)dtが定義できなくなります。デルタ関数を形式的に関数をみなして計算すると、物理学の色々な問題を形式に解けて、かつ、正しい答えが出るために、電気回路学を含む物理学の世界でよく使われますが、その議論には数学的な厳密さがありません。デルタ関数を含む数式を、数学的に厳密に扱うためには、超関数の概念を導入する必要がありますが、ここではそこまで立ち入りません。
デルタ関数の性質を把握したところで、リレーのコイルに発生するサージ電圧をデルタ関数を使って表す事を考えます。
図28のdidtをデルタ関数を使って数式化すると、式(18)になります。
式(2)に式(5)、式(6)、および式(18)を代入すると、コイルに掛かる電圧vは、式(19)および式(20)の様に求まります。
式(19)と式(20)より、vの波形をグラフ化すると、図32の様になります。
t=0におけるvの値は、−LERではなく、−∞です。
図32に示す様に、理論的には、時刻t=0におけるコイルの電圧は−∞で、その持続時間は0(無限小)です。しかし、実際には−∞という電圧は存在しません。
現実の世界では、先に述べたように、t=0および、その直後わずかな時間だけスイッチSW1の接点に火花放電が起きるなどして、電流は急に0になるのではなく有限の時間で0になります。そのためコイル電流iは図22の様にt=0でいきなり0にはならず、図33の様に、非常に短いものの有限の時間を掛けて0になります。
このため、t=0におけるdidtは−∞にはならずに、非常に絶対値が大きいものの、有限の値になります。その影響で、コイルに発生するサージ電圧(のピーク電圧の絶対値)は∞にはならずに、電源電圧の数十倍程度になります。
さらにいうと、ONの状態からOFFの状態にすんなりと1回で移行するのは、機械式のスイッチ(半導体を使わないスイッチ)では水銀スイッチなどのかなり特殊なスイッチに限られます。ほとんどの機械式のスイッチでは、バウンスが発生しますので、ONの状態からOFFの状態に移行する際に、何度もONとOFFを繰り返します。そのため、サージ波形はかなり複雑な波形になります。
式(17)が成立する事を、式(17)の左辺に式(15)を代入する事により確かめてみましょう。
式(17)の左辺に式(15)を代入して変形すると、式(21)の様になります。
この様に、計算結果が式(17)の右辺と一致します。
今回はリレーのコイルで発生するサージ電圧について説明しますが、次回はサージ電圧の対策について説明する予定です。続きを書くのはぼちぼちと。
