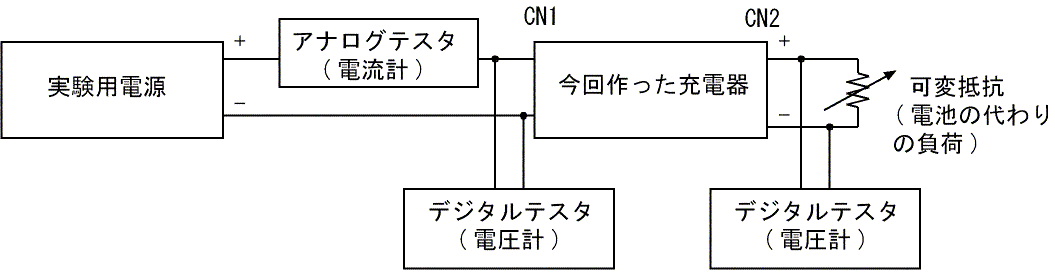
今回作成した充電器の電流-電圧特性を測りました。測定は下図の様な測定系で行いました。

使用機材の一覧表を次の表に示します。
| 機材の種類 | 機材の型番・仕様 |
|---|---|
| 実験用電源 | KIKUSUI PMC18-3A |
| アナログテスタ | SANWA KIT-8D |
| デジタルテスタ | SOAR 3510 |
| 可変抵抗 | 47Ω1/4Wの抵抗を複数並列に接続 |
測定風景を次の写真に示します。
図18の測定系には、電圧計として使うデジタルテスタを2台書きましたが、別に両方の電圧を同時に測る必要はないので、1台のデジタルテスタを、電源側と負荷側に付け替えて使っています。
画面下側中央に、抵抗負荷が写っています。47Ωの抵抗を多数並列につないでいます(物々しいですね) が、抵抗の本数で負荷抵抗を調整しています。本当の可変抵抗(ボリューム)を負荷にする場合は、許容損失(どのぐらいの発熱に耐えられるか)をよく考えないと、発煙などの事故が起こります。
写真では実験用電源のパネルに5.24Vと表示されていますが、デジタルテスタの表示は5.00Vとなっています。電圧の不一致は、実験用電源の電圧表示の精度がよくないせいもあるのですが、一番大きな理由は、電流計として使っているアナログテスタの内部抵抗による電圧降下です。実験用電源の表示電圧は、電圧調整時に参考にはなりますが、実験結果としては使えません。
入力電圧(CN1の電圧)を5V一定にし、負荷抵抗を変化させた場合の電流-電圧特性の測定結果を次の表に示します。
| 負荷抵抗[Ω] | 入力電圧[V] | 入力電流[mA] | 出力電圧[V] | 出力電流[mA] | 効率[%] |
|---|---|---|---|---|---|
| ∞ | 5.00 | 1.98 | 1.457 | 0 | 0.0 |
| 47.0 | 5.00 | 15.5 | 1.458 | 31.0 | 58.5 |
| 23.5 | 5.00 | 30.4 | 1.456 | 62.0 | 59.3 |
| 15.7 | 5.00 | 47 | 1.458 | 93.1 | 57.7 |
| 11.8 | 5.00 | 66 | 1.455 | 124 | 54.6 |
| 9.40 | 5.00 | 86 | 1.453 | 155 | 52.2 |
| 7.83 | 5.00 | 107 | 1.450 | 185 | 50.2 |
| 6.71 | 5.00 | 126 | 1.423 | 212 | 47.9 |
| 5.88 | 5.00 | 127 | 1.309 | 222 | 46.0 |
| 5.22 | 5.00 | 120 | 1.175 | 225 | 44.0 |
| 4.70 | 5.00 | 115 | 1.060 | 226 | 41.6 |
| 4.27 | 5.00 | 110 | 0.966 | 226 | 39.7 |
| 3.92 | 5.00 | 106 | 0.886 | 226 | 37.8 |
| 3.62 | 5.00 | 103 | 0.820 | 226 | 36.1 |
上の表の中で、実際に測定器で測定した数値は、入力電圧、入力電流、出力電圧の3つです。残りは計算で求めた数値です。
負荷抵抗は47Ωを、並列につないだ本数で割れば求まります。精度5%の抵抗を実験に使いましたので、公称値の47Ωを計算に使うと少し誤差が出ますが、0.1Ω単位でしか測れないデジタルテスタで抵抗値を実測するよりは精度がいいと思われるので、負荷抵抗は計算で求めました。
出力電流は、出力電圧を負荷抵抗で割れば求まります。
効率は、実験用電源から入力した電力の内、何%が負荷に供給されているかを示しています。入力電力は、入力電圧と入力電流の積で求まります。出力電力(負荷電力)は、出力電圧と出力電流の積で求まります。出力電力を入力電圧で割って、100をかければ効率が%の単位で求まります。
表を見ても実験結果が分かりにくいので、グラフにしたのが下の図です。
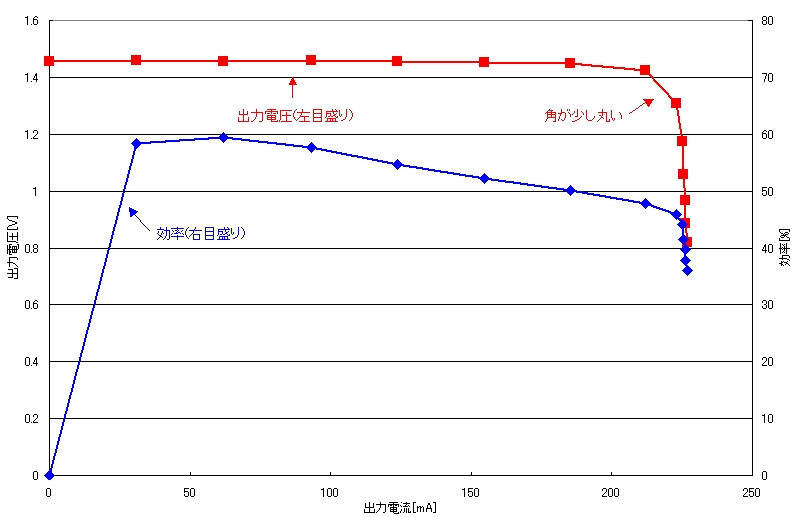
まず、赤い曲線に注目してください。これは、出力電流と出力電圧の関係を表したグラフです。理想的には定電流定電圧特性になりますが、おおむねその通りになっていることが分かります。定電圧域では、約1.45Vでほぼ電圧が一定になっています。定電流域では220mA強でほぼ電流が一定になっています。
定電流域の電流は、設計上は200mAです。実際に測ると1割強多くなっていますが、あまり充電電流は正確に設定しなくても、問題なく充電できます。一方で、定電圧域の電圧は、正確に設定しないと、過充電や不足充電になってしまいます。充電終止電圧は微調整できるのに、充電電流の方は微調整できない設計になっているのはそのためです。
また、上のグラフでは、定電圧域と定電流域の境目で、角が少し丸くなったグラフになっていますが、この程度なら充電に問題ありません。角が丸い特性になるのは、少数のトランジスタで回路を組んだため、誤差アンプの利得が高く取れなかったからです。オペアンプなどを使って同様の回路を設計すると、教科書どおりの角がとがった定電流定電圧特性が得られます。
次に青い曲線に注目してください。これは、入ってきた電力の内、何%を電池に供給できるかを表したグラフです。ステップダウンレギュレータの場合、理論的な効率は100%になると先に述べましたが、実際には色々な理由で電力のロスが発生します。今回製作した充電器では、出力電流によって効率は変化するものの、50%前後の効率(最もよい条件では59.3%)になっています。
電力ロス発生の理由は、例えば次の様なものが考えられます。
電力ロス発生の仕組みは、後にもう少し詳しく説明する予定ですが、1.45Vといった低い電圧のスイッチング電源は、効率を上げるのが難しいのです。今回製作した充電器でも、出力電圧が低くなるほど効率が下がっている傾向が、グラフから読み取れます。
余談になりますが、パソコンに使われるCPUの電源電圧は、年々下がっており、最近では1V程度になっています。(昔のCPUは5Vで動くものが多かったです。今でも、Arduinoなどのマイコンでは、5VのCPUが使われる場合があります) そのため、パソコンに使われるスイッチング電源の効率を上げるのに、以前よりも設計が難しくなってきています。
50%の効率はあまり高くないように思えるかも知れません。しかし、5Vの入力で1.45Vの出力が得られるシリーズレギュレータを作ったとすると、効率の理論限界値が1.45÷5×100=29%ですから、今回の充電器はそれよりも十分高い効率が得られていることが分かります。
今回はICを使わずに、トランジスタだけで設計するというコンセプトで充電器を作りました。トランジスタだけでもっと効率の高い充電器を作るとなると、部品数が大幅に増えるので、効率面では妥協した設計になっています。
また出力電圧を一定とすると、入力電圧が高くなるほどシリーズレギュレータの効率が悪くなります。入力が10Vだと、シリーズレギュレータの効率の理論限界値は1.45÷10×100=14.5%まで悪くなります。この後示すように、ステップダウンレギュレータを用いた今回の充電器では、電源電圧を10Vまで上げても、顕著な効率低下はありません。
次のグラフは、入力電圧が10Vの場合の特性を表しています。
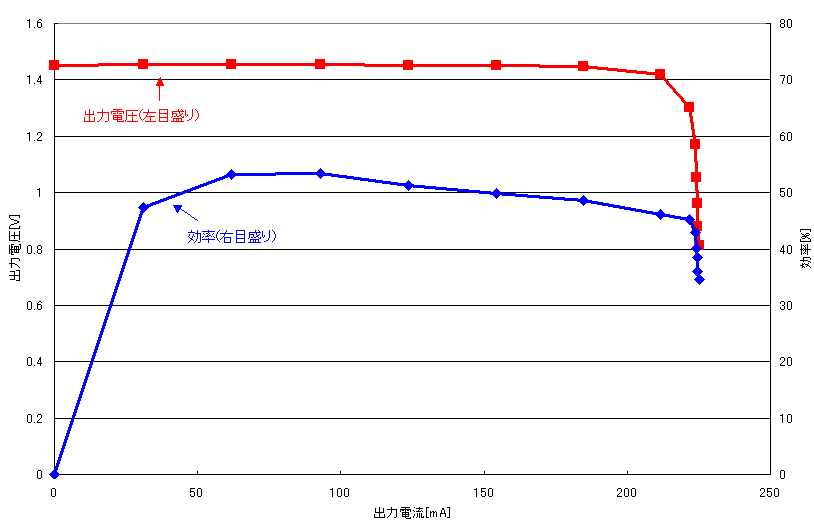
入力電圧が5Vの場合のグラフと比較すると、効率(青色の曲線)がわずかに低下する傾向にはありますが、電流-電圧特性(赤色の曲線)は、ほとんど一緒になっています。特に、定電圧領域での出力電圧が、入力電圧の変化をほとんど受けていないことが、電池を充電する上で重要になります。
この様に、特性が入力電圧の影響をほとんど受けないので、例えば5VのACアダプタで充電終止電圧を調整した充電器に、12VのACアダプタをつないで使っても、全く問題なく電池の充電ができます。この様な安定した特性を少数のトランジスタで実現するのには工夫が必要なのですが、後にその工夫について説明する予定です。
本当は、気温が上昇するにしたがって出力電圧が下がる様子も実験で確かめたかったのですが、恒温槽がないため、正確な実験ができませんでした。ただ、春に回路を組み立てた時に1.45Vに調整したはずの充電器が、初夏の今では1.43V位に下がっているので、温度上昇に対して電圧が下がる様子を実感しています。(図19、図20の特性は、回路を組み立てた直後に測定したので、充電終止電圧が約1.45Vになっています)また、ドライヤーで回路を暖めたら、電圧が下がることも確認しました。実験では正確に求められませんでしたが、SPICEによるシミュレーションでは、-4.7mV/℃の温度係数を持っているはずです。
後日談:電子負荷を作成したので、負荷条件を自由に変えられるようになりました。図19と図20の特性を電子負荷で測ると、より滑らかなグラフが得られるようになりました。詳しくは電子負荷の製作(2)の記事をご覧ください。
次のページでは、充電時の電池の電流・電圧の変化について書きます。
