| 2019年12月23日 | 公開 |
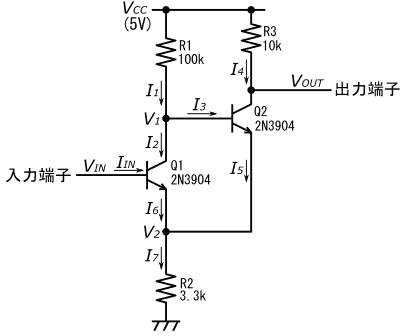
5ページの図48の、NPNトランジスタで構成した非反転型シュミットトリガ回路の動作について、引き続き解説します。
VINを0Vから少しずつ上げて行き、VTLHに達すると、図48のQ1のベース-エミッタ間電圧が0.7Vになり、Q1は活性領域に移行します。
活性領域に入ったQ1には、ベース電流IINが流れ始め、それに伴って、式(49)に従う形でコレクタ電流I2が流れ始めます。
ここで、hFE(Q1)は、活性領域におけるQ1のエミッタ接地電流増幅率を表しています。
またQ1のエミッタ電流I6は、キルヒホッフの電流則と式(49)より、式(50)に従って流れます。
この様に、Q1が活性領域に入って、Q1の各端子に電流が流れ始めるので、もはや図50、図51、および図52の等価回路は使えなくなります。今はもともとの回路図(図48)に立ち返って考える必要があります。
ここで、次の様に面白い現象が起こります。
この様に、2つのトランジスタQ1とQ2の間で正帰還が掛かり、I2の増加やI5の減少が短時間で一気に進みます。
ただし、NPNトランジスタに流れる電流の極性を考えると、I5は負の値にはなれません。I5が0に達した時点で、先ほどの正帰還のループが解消します。その時、I5=0になるので、Q2は遮断領域に移行します。
Q2が遮断領域に入ったという事は、Q2のどの端子にも電流が流れないという事です。つまり、式(51)が成立します。
この様に正帰還のループが解消した後は、I4が流れないためR3に電圧降下が生じず、出力電圧VOUTはVCCとなります。
VIN<VTLHの時はVOUT=VL(<VCC)だった(式(29)参照)ので、VIN=VTLHになるとVOUTがVCCにまで跳ね上がる事になります。つまり、この瞬間に入力がHと認識されたのです。
よって入力がHと認識された時の出力電圧VHは、式(52)で与えられます。
正帰還のループが解消すると、Q2が遮断領域に移行するだけではありません。実はたいていの場合、Q1も活性領域から飽和領域に移行します。この理由については、話の本筋ではないので、この直後のコラムで紹介します。
Q2が遮断領域に移行してQ2の端子に電流が流れなくなると、トランジスタQ1の動作にQ2は関係がなくなるので、Q1の動作の解析には、図48の回路からQ2とR3を取り除いた図53の等価回路を使う事ができます。
今、Q1が活性領域にあるか、飽和領域にあるかが問題になっているのですが、仮に活性領域にあるとします。(背理法を使って、Q1が活性領域にあると仮定して、矛盾が生じる事を示します)
Q1が活性領域にあるなら、I2は式(49)に従い、I6は式(50)に従うはずです。
Q1のコレクタ電流I2はベース電流IINのhFE(Q1)倍で、エミッタ電流I6はIINのhFE(Q1)+1倍ですが、NPNトランジスタのエミッタ接地電流増幅率hFEは、トランジスタの型番や個体差により変わるものの、おおむね数十から数百の値を取ります。
そこでhFE(Q1)>>1とすると、hFE(Q1)も、hFE(Q1)+1も、ほぼ同じ値とみなせますから、式(53)が成立します。
Q1のコレクタ電圧V1は、式(24)と式(53)より、式(54)で表わす事ができます。
Q1のエミッタ電圧V2は、式(26)より、式(55)で表す事ができます。
Q1のコレクタ-エミッタ間電圧V1−V2は、式(54)と(55)より、式(56)の様に求まります。
Q1が活性領域にあるというのは、コレクタ-エミッタ間電圧V1-V2が0より大きい事ですから、Q1が活性領域にあるためには、式(57)が成立する必要があります。
一方でI6は、Q1が活性領域にあっても、遮断領域にあっても、式(58)で求まります。
注:今VIN=VTLHの場合の話をしているので、V2≒VTLH−0.7[V]としています。
式(45)を式(58)に代入してI6を求めると、式(59)の様になります。
この式を式(57)に代入すると、式(60)が得られます。
VCCは普通、0.7Vよりかなり高く設定しますから、R1がかなり小さくないと、式(60)の条件は成立しません。
例えば、図48の定数と同様に、R2=3.3[kΩ]、R3=10[kΩ]、VCC=5[V]とすると、R1<2.96[kΩ]とR3よりかなり小さな値にならないと、式(60)の条件は成立しません。この様にR1<<R3という条件においては、ヒステリシス(ヒステリシスの求め方は後述)が小さくなりすぎ、シュミットトリガ回路としては、使いにくいのです。
そのため、抵抗値やVCCを常識的な値に設定すると、たいていは式(60)が成立せずに、Q1が活性領域にあるという仮定と矛盾します。そのためQ1は、Q2が遮断領域に移行した瞬間に、遮断領域に移行します。
抵抗値やVCCを常識的な値に設定するとQ1が遮断領域に移行する(式(60)が成立しない)とはいうものの、一応、式(60)の逆の条件である式(61)が、図48のシュミットトリガ回路が正常に動作するための必要条件となります。
VINがさらに増加して、VIN>VTHLとなった場合に、図48の回路で何が起こるかを考えてみましょう。
VIN=VTHLの時の回路の状態で説明した様に、VIN=VTHLとなった直後には、Q1は飽和領域にあり、Q2は遮断領域にあります。
さらにVINが増加すると、Q1のベース電流IINがさらに増加し、Q1は引き続き飽和領域にとどまります。
またQ1が飽和領域にあると、Q2のベース・エミッタ間電圧が、Q1によってほぼ0Vに維持されるので、Q2は引き続き遮断領域にとどまります。
Q2が遮断領域にあるので、図53の等価回路を使ってQ1の動作を解析する事ができます。
この時、出力電圧は、式(52)で与えられるVH(つまりVCC)になっています。
ここで、入力電流IINについて考えてみましょう。
図53のQ1は飽和領域にあるので、式(62)と式(63)が成立します。
Q1が飽和領域にあり、式(62)と式(63)が成立する事を利用すると、図53の等価回路は、さらに図54の様に簡略化できます。
オームの法則よりI6を求めると、式(64)の様に求まります。
オームの法則よりI1を求めると、式(65)の様になります。
キルヒホッフの電流則より、式(66)の関係が成立します。
式(66)に式(64)と式(65)を代入すると、IINは式(67)の様に求まります。
式(67)から、VINが1V増加するごとに、IINがR1+R2R1R2[A]増加する事が分かります。よって、VIN>VLTHの場合の図48のシュミットトリガ回路の入力インピーダンスをZINHとすると、ZINHは式(68)の様に求まります。
注:R1//R2は、R1とR2の抵抗値を持つ2つの抵抗を、並列接続した時の抵抗値を表しています。
式(68)にR1=100[kΩ]とR2=3.3[kΩ]を代入して、ZINHを計算すると、約3.19kΩになります。
VINが0Vから上昇してVTLHに達するまでの、入力がLと認識されている期間に、入力インピーダンスZINLが無限大だった事(式(48)を参照)を思い出してください。式(68)より、VINがVTLHを超えて入力がHと認識される様になると、入力インピーダンスがR1//R2に急減する事が分かります。図48のシュミットトリガ回路の入力に、出力インピーダンスが低い回路を接続する場合は、図48の入力端子に抵抗を接続して入力インピーダンスを上げるなどの対策が必要になる場合があります。
次のページでは、入力電圧が、Hと認識される高い電圧からLと認識される低い電圧へと低下する際の、回路の状態について説明します。
