| 2019年12月22日 | 公開 |
この章では、シュミットトリガ回路を作るにはどうしたら良いかを解説します。
この節ではバイポーラトランジスタの一種であるNPNトランジスタにより、シュミットトリガ回路を構成する方法について説明します。電圧と電流の極性を逆にすれば、PNPトランジスタでもシュミットトリガ回路を構成できますが、ここでは述べません。
なお、動作原理にはあまり興味はなく、NPNトランジスタを用いたシュミットトリガ回路の回路定数から、回路の特性を計算するための式を、手っ取り早く知りたい人は、8ページからご覧ください。
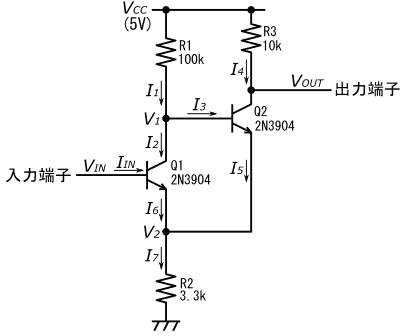
図48の回路は、バイポーラトランジスタの一種であるNPNトランジスタで非反転型シュミットトリガ回路を構成した一例です。
図48の回路の入出力電圧特性はおおよそ図49の様になります。
電源電圧VCCは5V、入力電圧が上昇する際に、Lだった入力がHと認識され始める閾値VTLHは約2.0V、入力電圧が低下する際に、Hだった入力がLと認識され始める閾値VTHLは約0.8Vで、2.0−0.8=1.2V程度のヒステリシスがあります。また、出力がHの時の出力電圧VHは5Vで、出力がLの時の出力電圧VLは約1.3Vです。
図48の回路の動作について考えてみましょう。部品番号R1、R2、およびR3の抵抗の抵抗値をそれぞれR1、R2、およびR3として議論します。
まず入力電圧VINが0Vの場合について説明します。
VIN=0[V]で、I7の電流の向きを考えると、トランジスタQ1のエミッタ電圧V2は0または正の値になるはずです。よって、Q1のベース-エミッタ間電圧VIN−V2は0または負の値になります。Q1のベース-エミッタ間電圧が0.7Vに満たないので、Q1は遮断領域(トランジスタのどの端子にも電流が流れない動作領域)にある事が分かります。
よって、式(20)が成り立ちます。
この様に、Q1の全ての端子に電流が流れないので、この時トランジスタQ2の動作の解析をするには、図48のシュミットトリガ回路からQ1を除いた、図50の等価回路で行っても良い事が分かります。
この図を見ると、I3(=I1)がQ2のベースに流れ込むため、Q2のコレクタ・エミッタ間が導通し、Q2は飽和領域(コレクタ-エミッタ間の電圧がほぼ0となる動作領域)にある事が分かります。
注:図50において、Q2が飽和領域にあるためには、ある条件が必要です。その条件を満たさないと、Q2は活性領域(コレクタ・エミッタ間が導通しているものの、コレクタ・エミッタ間電圧が0よりも大きい動作領域)に入ってしまいます。この条件については後のコラムで述べますが、図50の抵抗値の設定では、Q2は飽和領域に入ります。
Q2が飽和領域内にあるので、式(21)と式(22)が成立します。
注:NPNトランジスタが飽和領域にあっても、コレクタ-エミッタ間電圧は完全に0Vになるわけではなく、0.1~0.3V程度の低い電圧が残ります。この電圧の事をコレクタ-エミッタ間飽和電圧といい、VCE(SAT)という記号で表わす事が多いです。式(21)では、このVCE(SAT)を無視して式を作っています。厳密にはVOUT=V2+VCE(SAT)となります。
これら2式から、図50の等価回路は、さらに図51に書き換えられる事が分かります。
ここで、R1>>R3となっている事を利用すると、I1<<I4となる事から、I1を無視した図52の回路で考えても、VOUT(≒V2)およびI4の計算値にはあまり影響しない事が分かります。
ここまで回路を簡略化すると、これはVCCをR2とR3で分圧する回路ですから、出力電圧VOUTは式(23)で求まる事が分かります。
図52や式(23)の様に、I1を無視してVCCを求めると、求まったVCCの精度は低いものの、式が簡単なため、回路の動作の大まかな理解や、回路設計時の大まかな定数の決定には役に立ちます。
式(23)にR2=3.3[kΩ]、R3=10[kΩ]、VCC=5[V]を代入すると、VOUT≒1.241[V]となります。
次に、R1>>R3の条件を使わず、I1を無視しない図51の回路でVCCを求めてみましょう。
キルヒホッフの電圧則とオームの法則より、V1は式(24)で求まります。
注:式(24)は、図51だけではなく、図48でも成立するので、Q1が遮断領域にある事や、Q2が飽和領域にある事を前提にしないでも成立する式です。
同様にVOUTも、キルヒホッフの電圧則とオームの法則より、式(25)の様に求まります。
注:式(25)は、図51だけではなく、図48でも成立するので、Q1が遮断領域にある事や、Q2が飽和領域にある事を前提にしないでも成立する式です。
V2がR2の両端電圧である事を考えると、オームの法則より、V2は式(26)の様に求まります。
注:式(26)は、図51だけではなく、図48でも成立するので、Q1が遮断領域にある事や、Q2が飽和領域にある事を前提にしないでも成立する式です。
図51でキルヒホッフの電流則より、式(27)が成立します。
注:式(27)は、図51だけではなく、図50でも成立するので、Q2が飽和領域にある事を前提にしないでも成立する式です。
式(21)、式(22)、および式(24)~式(27)の6つの式を連立させて、V1、V2、I1、I4、I7の5つの変数を消し、VOUTを求めると、式(28)が得られます。
また、式(28)で求まるVOUTは、出力がLの場合の出力電圧VLとなります。
以上をまとめると、VIN=0[V]の場合の出力電圧VOUTは、VLとなり、VLは式(29)で求まります。
さらに、R1>>R3が成立してI1が無視できる場合は、式(29)は、式(30)の様に簡略化できます。
式(29)にR1=100[kΩ]、R2=3.3[kΩ]、R3=10[kΩ]、VCC=5[V]を代入すると、VL≒1.315[V]となります。 式(30)は、I1を無視して求めた荒い近似式ですが、この式に抵抗値やVCCの値を代入すると、VL≒1.241[V]と、I1を無視しないで求めた式(29)の1.315Vよりも、わずか0.074V低い値となっており、実用的な近似精度になっています。
式(21)よりV2≒VOUTが成立しますから、VIN=0[V]の時のV2は式(31)の様に求まります。
図50の等価回路において、R1が大きすぎて、Q2のベース電流I1が不足した場合、R2やR3に十分な電圧降下を発生させられず、Q2は活性領域に入ってしまいます。そこで、Q2が飽和領域に入るための条件を考えてみます。
ここでは、Q1が活性領域に入ると仮定して、その時に成立する条件を求め、その反対の条件からQ1が飽和領域に入る条件を求めます。(背理法)
Q1が活性領域にあると仮定すると、I4とI5は、それぞれ式(32)と式(33)で求まります。
ここで、hFE(Q2)はQ2のエミッタ接地電流増幅率を表しています。NPNトランジスタのエミッタ接地増幅率は、トランジスタの型番や個体差により異なるものの、おおよそ数十から数百の値となるため、hFE(Q2)>>1が成立すると考えても構いません。そうするとhFE(Q2)もhFE(Q2)+1も同じ様な値になるので、式(34)が成立します。
また、Q2のベース電流I1は、式(35)で求まります。
Q2のコレクタ電圧VOUTは、キルヒホッフの電圧則とオームの法則より、式(36)の様に求まります。
またQ2のエミッタ電圧V2は、オームの法則より、式(37)の様に求まります。
式(36)と式(37)から、Q2のコレクタ-エミッタ間電圧VOUT−V2は、式(38)の様に求まります。
Q2が活性領域にあるという事は、Q2のコレクタ-エミッタ間電圧VOUT−V2が0より大きい事を意味しますから、式(39)が成立しているはずです。
式(39)に式(35)を代入すると、式(40)が得られます。
この式は複雑な式ですが、VCCが0.7Vより十分大きく、ベース-エミッタ間で発生する0.7Vが相対的に無視できる場合を考えると、式(40)の右辺第2項は無視できますので、式(41)の関係が得られます。
逆に式(41)が成立しないと、矛盾が発生しますから、Q2が活性領域にあるという仮定が間違っている事になります。
つまり、式(41)の逆の条件である式(42)が成立すると、Q2が飽和領域に入って、図48のシュミットトリガ回路が意図通り動作します。
VCC>>0.7[V]という条件を外してQ2が飽和領域に入る条件を求めると、式(40)の反対の、式(43)に示す条件になります。
式(43)は式(42)よりも厳密な式ですが、実際には使う事はないでしょう。
この議論ではhFE(Q2)は一定だという前提で議論をしていますが、実際には同じ型番のNPNトランジスタでもhFEにばらつきがかなりありますし、コレクタ-エミッタ間電圧や、コレクタ電流によっても、hFEは変動するからです。よって、式(42)や式(43)がぎりぎり成立する条件では回路を設計するべきではなく、余裕をもってこれらの式の条件を満たす様に抵抗値を設定する必要があります。
よって、式(43)の様な複雑な式を使って、厳密な計算を行う意味はあまりなく、式(42)の様な単純な式で、式の意味を把握するメリットの方が大きいといえます。
2N3904のデータシートによると、hFEは最小でも30ある様です。hFE(Q2)=30とR1=100[kΩ]とR3=10[kΩ]を式(42)に代入すると、左辺は100kΩで右辺は300kΩとなり、余裕を持って式(42)が成立する事が分かります。(これは最悪の状態を仮定しているので、hFEが30よりも大きければ、さらに余裕を持って式(42)を満たします)
後で分かる様に、R1はR3に対して大きくする方が、ヒステリシスが大きくできるので好ましいのですが、あまりR1をR3に対して大きくしすぎると、今度は式(42)を満たさなくなります。
そこで、とりあえずR1をR2の10倍以下に設定しておけば、たいていのNPNトランジスタで式(42)を満たします。
VINを0Vから少しずつ上げる場合について考えます。
式(31)よりVIN=0[V]の時のV2はVLとほぼ同じ値になります。よって、VINを少しずつ上げて行っても、図48においてVIN<VL+0.7[V]が成立している間は、Q1が遮断領域に入っており、式(20)が成立するため、図50や図51の等価回路が使えます。よって、式(23)と式(28)~式(31)は、そのまま成立します。
ここで、VIN<VL+0.7[V]が初めて成立しなくなり、Q1が遮断領域から外れてしまう入力電圧VTLHを求めます。
VTLHは、VIN<VL+0.7[V]が初めて成立しなくなるVINの値の事ですから、式(44)が成立します。
式(29)を式(44)に代入すると、式(45)の様にVTLHが求まります。
また、R1>>R3が成立すると、VLは式(30)の様に近似的に求められます。この時VTLHは、式(30)を式(44)に代入して求められる、式(46)で近似的に求まります。
R1=100[kΩ]、R2=3.3[kΩ]、R3=10[kΩ]、およびVCC=5[V]を式(45)および式(46)に代入すると、それぞれ2.015[V]、1.941[V]となります。
ここで、式(45)において、閾値VTLHが電源電圧VCC以上になると、電源電圧の範囲内の電圧は、全てLと認識される様になり、シュミットトリガ回路として使えなくなる事に注意が必要です。すなわち、式(47)が成立する様な範囲でR1、R2、R3、およびVCCを設定する必要があります。
注:式(47)はシュミットトリガ回路が正常に機能するための必要条件であり、十分条件ではではない事に注意が必要です。式(43)も、シュミットトリガ回路が正常に機能するための必要条件です。
参考:式(45)の代わりに式(46)をVTLH<VCCに代入しても、式(47)が導出されます。
また式(20)より、VINがVTLHに達するまでは、VINの値に関わらずIIN=0が成立するため、この範囲での図48のシュミットトリガ回路の入力インピーダンスをZINLとすると、ZINLは式(48)の通り求まります。
次のページでは、VINがVTLHに達して以降の、シュミットトリガ回路の動作について説明します。
