| 2020年01月03日 | 更新 |
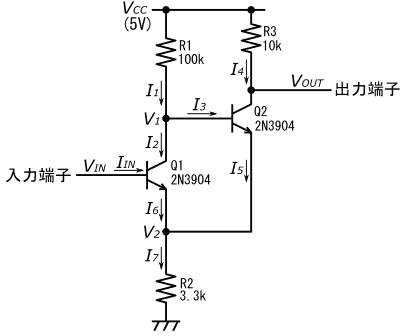
5ページの図48の、NPNトランジスタで構成した非反転型シュミットトリガ回路の動作について、引き続き解説します。
前のページでは、図48のNPNトランジスタで構成したシュミットトリガ回路の回路定数から、回路の動作を解析する方法について説明しました。
このページでは、逆に、シュミットトリガ回路の要求仕様(電源電圧VCC、入力がLからHに変わる時の閾値VTLH、および入力がHからLに変わる時の閾値VTLH)から、回路定数を求める方法、すなわちシュミットトリガ回路の設計法について説明します。
前のページの表5に、シュミットトリガ回路の回路定数から、シュミットトリガ回路の動作を解析するのに必要な式の一覧を挙げました。これらの式を基に、シュミットトリガ回路の設計に必要な式を導出します。
式(82)を変形すると、R1とR2の関係が、式(86)の様に求まります。
この式を変形すると、式(87)の様に、R2をR1を使って表す事もできます。
この式を式(45)に代入して、R2を消去すると、式(88)が得られます。
この式を変形すると、式(89)の様に、R1をR3を使って表す事もできます。
この式を式(87)に代入すると、式(90)が得られます。
この式を変形すると、式(91)が得られます。
式(87)を見ると、VCCとVTHLが与えられれば、R2とR1の比が決まる事が分かります。また式(88)を見ると、VCCとVTHLとVTLHが与えられれば、R3とR1の比が決まる事が分かります。
この様に、VCCとVTHLとVTLHが与えられてもR1とR2とR3の比が決まるだけで、R1やR2やR3の値そのものが決まる訳ではありません。つまり、VCCとVTHLとVTLH以外に、R1、R2、およびR3の、いずれかひとつの値を決めないと、回路を設計する事ができません。
注:R1、R2、およびR3の、いずれかひとつの値を決める代わりに、ZINHの値を決めて設計する方法もあります。この方法については後述します。
今、VCCとVTHLとVTLHが与えられているとして、さらにR1の値を自分で決めて、設計をする方法について考えます。この設計に使う式は、表11の様に、式(87)と式(88)になります。
| 定数 | 計算式 |
|---|---|
| R2 | R2≒VTHL−0.7[V]VCC−VTHLR1 ・・・ (87) |
| R3 | R3≒(VTHL−0.7[V])(VCC−VTLH+0.7[V])(VCC−0.7[V])(VTLH−VTHL)R1 ・・・ (88) |
VCC、VTLH、VTHL、およびR1の値を表11の2つの式に代入すると、R2とR3が求まる事が、式からお分かりになるでしょう。
ただし、VCC、VTLH、VTHLは、式(92)を満たす様に決める必要があります。
参考:VTHL>0.7[V]が成立している必要があるのは、式(82)より、R1を任意の正の値に固定し、R2を0~∞の範囲で変化させた場合に、R2=0において、VTHLが最低値0.7Vを取るからです。R2=0ならば、式(45)および式(82)よりVTLH=VTHL=0.7[V]となり、ヒステリシスがなくなってしまい、シュミットトリガ回路として動作しません。(式(92)を満たしません) よって、VTHL≧0.7[V]ではなく、VTHL>0.7[V]が成り立つ必要があります。式(82)においてVTHLがR2=0で最低値0.7Vを取る事が理解しにくいなら、式(82)を式(93)の様に変形すると分かり易いです。R2が0~∞の範囲で変化すると、R2R1+R2は0~1の範囲で単調に変化し、その結果、VTHLは0.7V~VCCの範囲を単調に変化する事がこの式から分かります。そしてVTHLが最低値0.7を取るのは、R2R1+R2=0、すなわちR2=0の時のみです。
また当然の事ですが、R1は正の数である必要があります。つまり、式(94)が成立している必要があります。
参考:式(92)と式(94)が成立していれば、R2>0とR3>0は自動的に成立します。
それでは、例として、VCC=5[V]、VTLH=1.9[V]、VTHL=1.1[V]、R1=33[kΩ]の条件で設計してみましょう。(表12参照)
| 定数の種類 | 定数の値 |
|---|---|
| VCC | 5V |
| VTLH | 1.9V |
| VTHL | 1.1V |
| R1 | 33kΩ |
これらの値を表11の2つの式に代入すると、R2とR3の値は表13の通り求まります。よって、設計した回路の回路図は図61の様になります。(使用するトランジスタとして2N3904を使う事を仮定しています)
| 抵抗 | 抵抗値 |
|---|---|
| R2 | 3.385kΩ |
| R3 | 14.58kΩ |
VCC=5[V]、R1=33[kΩ]、R2=3.385[kΩ]、R3=14.58[kΩ]、hFE(Q2)=30(2N3904のhFEの最小値)を表6の3つの式に代入すると、表14の様に制約条件が求まります。
| 制約条件の式番号 | 制約条件の計算結果 | 合否 |
|---|---|---|
| 式(43) | R1≦362.0[kΩ] | 合 |
| 式(47) | R2<89.57[kΩ] | 合 |
| 式(61) | R1≧3.840[kΩ] | 合 |
この表から分かる様に、図61の回路は、表6の3つの制約条件をすべて満たします。
参考:表13や表14の計算結果を得るためには、関数電卓等で計算すると、時間がかかる計算が必要ですが、バイポーラトランジスタを用いたシュミットトリガ回路の動作解析・設計サービスというオンラインサービスを使うと、簡単に計算できます。
確認のために、図61の回路をTLspiceでシミュレーションして、VTLHとVTHLを求めた結果を表15に示します。
| 閾値の種類 | LTspiceで求めた値 [V] |
要求仕様の値 [V] |
誤差 [V] |
|---|---|---|---|
| VTLH |
1.789 |
1.9 |
−0.111 |
| VTHL | 1.026 |
1.1 | −0.074 |
この様に、LTspiceのシミュレーション結果は、おおむね要求仕様通りになっています。
2番目の設計例として、設計例1と同様にVCC=5[V]、R1=33[kΩ]とし、一方で閾値はVTLH=4[V]、VTHL=1[V]と変更してヒステリシスを大きく取った条件で設計してみます。(表16参照)
| 定数の種類 | 定数の値 |
|---|---|
| VCC | 5V |
| VTLH | 4V |
| VTHL | 1V |
| R1 | 33kΩ |
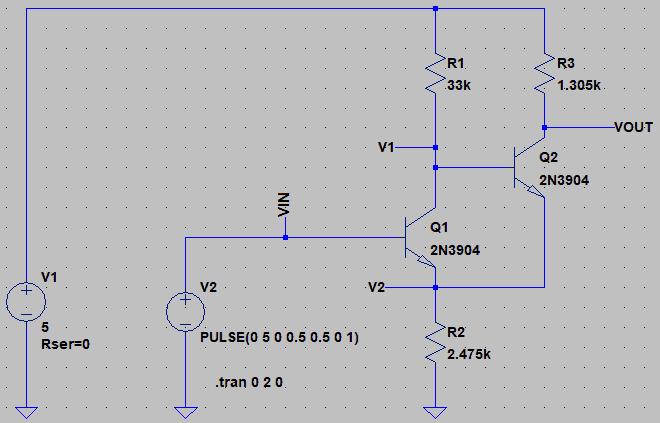
これらの値を表11の2つの式に代入すると、R2とR3の値は表17の通り求まります。R1~R3の抵抗値を書き込んだ回路図は図62の様になります。
| 抵抗 | 抵抗値 |
|---|---|
| R2 | 2.475kΩ |
| R3 | 1.305kΩ |
VCC=5[V]、R1=33[kΩ]、R2=2.475[kΩ]、R3=1.305[kΩ]、hFE(Q2)=30(2N3904のhFEの最小値)を表6の3つの式に代入すると、表18の様に制約条件が求まります。
| 制約条件の式番号 | 制約条件の計算結果 | 合否 |
|---|---|---|
| 式(43) | R1≦23.27[kΩ] | 否 |
| 式(47) | R2<8.014[kΩ] | 合 |
| 式(61) | R1≧769.9[Ω] | 合 |
この様に、図62の回路は、式(43)の制約条件を、わずかですが、満たしていません。そのため、図62の回路は正常に動作しない可能性があります。
この様に設計が失敗するのは、表16の要求仕様の中でも特にVTLHとVTHLに無理があるからです。
注:表16の要求仕様の中で、R1の値だけは、何Ωを指定しても、制約条件を満たすかどうかには関係ありません。これは、VCCとVTLHとVTHLの3つの要求仕様が決まれば、R1とR2とR3の比が決まる事と、表6の制約条件の式は、R1とR2とR3の比に課される制約条件である事によります。
この場合(設計例2の場合)は、ヒステリシス(VTLH−VTHL)を大きく取りすぎたために、式(43)を満たさなくなったのです。計算してみると分かりますが、VTLHを3Vに下げるか、あるいはVTHLを2Vに上げるかして、ヒステリシスを2Vに下げると、表6の制約条件を全て満たす設計ができます。
先ほどは、図62の回路が式(43)の制約条件を満たさないために、設計が失敗したといいました。
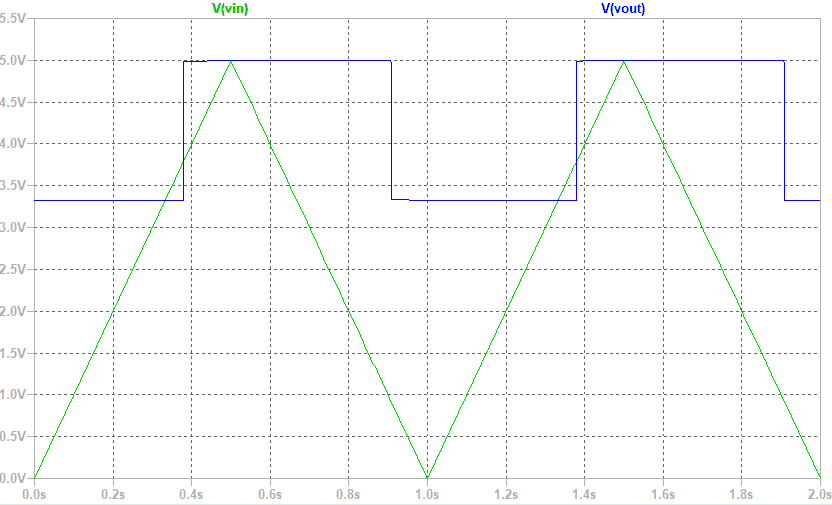
しかし、試しに図63の回路をLTspiceでシミュレーションすると、シュミットトリガ回路として動作する事が分かりますし(図63と図64を参照)、シミュレーション結果からVTLHとVTHLを求めると、表19に示す様に、要求仕様にそこそこ近い値が出ます。
| 閾値の種類 | LTspiceで求めた値 [V] |
要求仕様の値 [V] |
誤差 [V] |
|---|---|---|---|
| VTLH | 3.795 | 4 | −0.205 |
| VTHL | 0.921 | 1 | −0.079 |
これは、式(43)の制約条件を計算する場合に、2N3904のhFEの最小値である30を仮定している事と関係があると思われます。
LTspiceでのシミュレーションでは、hFEは最小値ではなく典型値(標準値)に近い値に設定した状態で計算が行われていると思います。仮に、hFE(Q2)=50として式(43)を計算し直すと、R1≦38.78[kΩ]という制約条件が出てくるのですが、この場合、R1(33kΩ)はこの制約条件を満たします。
また、式(43)の制約条件を満たさなくても、図48の回路がシュミットトリガ回路として動作しなくなる訳ではない事にも注意が必要です。
図48の回路が式(43)を満たさない場合、Q2が導通状態になっても飽和領域に移行せずに、活性領域にとどまります。飽和領域に移行せずに活性領域にとどまっても、シュミットトリガ回路としては動作するのですが、VLやVTLHの値が、Q2が飽和領域にあるとして計算した式(29)や式(45)で求める値からずれてくるのです。
さらにいうと、VLやVTLHの値が式(29)や式(45)とずれる度合いは、hFE(Q2)が低いほどひどくなります。
hFEの値がシュミットトリガ回路の動作に与える影響を検証するために便利な、BC847シリーズというNPNトランジスタのシリーズがあります。このシリーズのBC847A、BC847B、およびBC847Cという、hFEのみが異なり、他の特性はほぼ一緒の3種類のNPNトランジスタが、LTspiceの標準ライブラリに登録されています。
このBC847シリーズのトランジスタは、hFEによって3グループにランク分けされています。hFEが低い(hFEの最小値が110)グループにはBC847A、hFEが標準的な(hFEの最小値が200)グループにはBC847B、hFEが高い(hFEの最小値が420)グループにはBC847Cという型番が付けられています。(表20参照)
| 型番 | hFEの最小値 (VCE=5[V]、IC=2[mA]) |
|---|---|
| BC847A | 110 |
| BC847B | 200 |
| BC847C | 420 |
注:表20の値は、nexperiaのBC847のページでダウンロードしたデータシートから引用しました。
このBC847シリーズを使って、表16の要求仕様でシュミットトリガ回路を設計すると、当然、2N3904で設計した場合と同様、表17に示すR2とR3の値になります。
ただ、BC847シリーズは2N3904よりhFEが高く、シリーズ中一番hFEが低いBC847Aでも、hFEの最小値が110もあります。hFE(Q2)=110として、式(43)の制約条件を計算しても、R1≦85.31[kΩ]となり、R1は制約条件を満たします。(当然、hFEが高いBC847BやBC847Cなら、式(43)の制約条件は、さらに余裕を持って満たします)
図62の回路のトランジスタをBC847Aに取り換えた場合と、BC847Cに取り換えた場合の2通りについて、LTspiceでシミュレーションを行いVTLHとVTLHを求めた結果を表21に示します。
| 閾値の種類 |
BC847Aでシミュレーションして求めた値
[V] |
BC847Cでシミュレーションして求めた値
[V] |
要求仕様の値 [V] |
|---|---|---|---|
| VTLH | 3.786 | 3.784 | 4 |
| VTHL | 0.918 | 0.897 | 1 |
この結果から、図63の回路のトランジスタをBC847Aに換えても、BC847Cに換えても、ほぼ同じ動作をする事が分かります。VTLHの値としては0.002V、VTHLの値としては0.021Vしか違いません。
ところが、より条件の厳しい、表22に示す要求仕様で設計すると、話が変わってきます。表22の要求仕様で行う設計を設計例3とします。
| 定数の種類 | 定数の値 |
|---|---|
| VCC | 5V |
| VTLH | 4V |
| VTHL | 0.75V |
| R1 | 33kΩ |
表22は、表16と比較すると、VTHLだけが1Vから0.75Vに変わっています。
表22の条件で設計すると、R1とR2の値は表23の様になり、回路図は図65の様になります。
| 抵抗 | 抵抗値 |
|---|---|
| R2 | 338.2Ω |
| R3 | 200.7Ω |
VCCとR1については表22の値を使い、R2とR2については表23の値を使い、BC847Aを想定してhFE(Q2)=110として表6の制約条件を計算すると、表24の様になります。
| 制約条件の式番号 | 制約条件の計算結果 | 合否 |
|---|---|---|
| 式(43) | R1≦13.01[kΩ] | 否 |
| 式(47) | R2<1.233[kΩ] | 合 |
| 式(61) | R1≧119.4[Ω] | 合 |
この様に、BC847AのhFEの最小値である110を用いて計算した場合は、式(43)の制約条件を満たしません。
注:BC847Aでも、hFEが110より大きい個体があり、またICの値などによってもhFEが変化しますので、必ずBC847Aが式(43)の制約条件を満たさない事を保証しているわけではありません。
一方で、VCCとR1については表22の値を使い、R2とR2については表23の値を使い、BC847Cを想定してhFE(Q2)=420として表6の制約条件を計算すると、表25の様になります。
| 制約条件の式番号 | 制約条件の計算結果 | 合否 |
|---|---|---|
| 式(43) |
R1≦49.67[kΩ] | 合 |
| 式(47) | R2<1.233[kΩ] | 合 |
| 式(61) | R1≧119.4[Ω] | 合 |
この様に、BC847Cを使う場合は、hFEとして最小値の420を使って計算しても、式(43)の制約条件を満たします。
図65の回路のトランジスタをBC847Aとした場合とBC847Cとした場合の2通りについて、LTspiceでVTLHとVTHLの値を求めた結果を表26に示します。
| 閾値の種類 |
BC847Aでシミュレーションして求めた値
[V] |
BC847Cでシミュレーションして求めた値
[V] |
要求仕様の値 [V] |
|---|---|---|---|
| VTLH | 3.313 | 3.711 | 4 |
| VTHL | 0.653 | 0.631 | 0.75 |
この結果を見ると、(hFEを最小値とした場合では)制約条件を満たさないBC847Aでシミュレーションして求めたVTLHの値が3.313Vとなっており、要求仕様の4Vより0.687Vも低くなっているのが目につきます。一方で、BC847Cでシミュレーションすると、VTLHの値が3.711Vとなっており、要求仕様の4Vより0.289Vしか低くなっていません。(VTHLの値については、BC847AでもBC847Cでも大差ありません)
式(48)を満たさないからといってもシュミットトリガ回路が動作しない訳ではないのですが、VTLHの値の要求仕様からの誤差が大きくなりますし、式(48)を満たさない回路は、トランジスタのhFEの値によって、回路動作に影響を受けやすい(トランジスタに対する素子感度が高い)回路なのです。
シュミットトリガ回路を量産した場合の回路特性のばらつきを抑えたいなら、式(43)の制約条件を、余裕を持って満たす事が要求されます。hFE(Q2)の値を、トランジスタのhFEの最小値より低めに見積もっても式(43)を満たす事が望ましいといえます。
極端にいえば、例えばhFE(Q2)=20と、かなり低めに設定して設計すると、たいていのトランジスタは20以上のhFEを持ちますので、使用するトランジスタのhFEをデータシートで調べる事なくシュミットトリガ回路を設計する事もできます。(その分、制約条件が厳しくなり、設計が失敗しやすくなります)
hFE(Q2)=20で動作する様に設計しておけば、シュミットトリガ回路に使っているトランジスタがディスコンになっても、パッド(ランド)形状の同じ別のトランジスタに容易に置き換えられますので、対応が簡単になります。
説明が長くなってきましたので、いったんここで話を区切ります。次回も、NPNトランジスタを用いたシュミットトリガ回路の設計法について説明します。続きは近日中に発表する予定です。
