| 2019年12月24日 | 公開 |
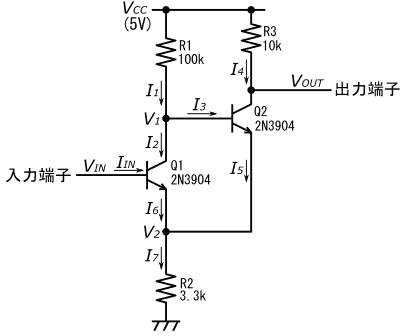
5ページの図48の、NPNトランジスタで構成した非反転型シュミットトリガ回路の動作について、引き続き解説します。
今度は、VIN>VTLHの状態(入力がHと認識されている状態)からVINを徐々に低下させる場合の回路の動作について考えます。
図48のシュミットトリガ回路において、最初の内は、Q1が飽和領域にあり、またQ2は遮断領域にあるため、図54の等価回路が使えます。
つまり出力電圧はVCCとなり、入力インピーダンスはR1//R2となります。
式(67)より、VINを低下させるとQ1のベース電流IINも低下する事が分かります。
あまりIINが低下すると、Q1を飽和させるほどの電流をR1とR2に流せなくなって、Q1が遮断領域から活性領域に移行します。
Q1が遮断領域から活性領域に移行する時点では、Q1が活性領域にあると仮定して求めたコレクタ-エミッタ間電圧V1−V2がちょうど0になっているはずです。(さらにVINが低下してQ1が活性領域に移行してしまうと、V1-V2>0となります)
V1−V2は、式(24)から式(26)を引く事により、式(69)の様に求まります。
Q1が活性領域にあると仮定した場合のI2とI6は、それぞれ式(49)と式(50)で求まりますから、これらの式を式(69)に代入すると、V1−V2は、IINを使って、式(70)の様に表現できます。
Q1が飽和領域から活性領域に移行する瞬間には、式(70)のV1−V2がほぼ0になるので、この式の左辺に0を代入する事により、IINは式(71)の様に求まります。
IINが求まったところで、Q1が遮断領域から活性領域に移行する瞬間のVINを求めます。Q1が活性領域に移行する瞬間には、Q1が遮断領域にある場合(式(63)参照)と同様に、式(72)が成立していると考えられます。
この式に、式(55)と式(50)を代入すると、式(73)が得られます。
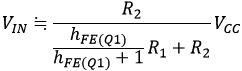
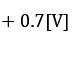
注:式(73)の導出には、hFE(Q1)>>1が成立しているものとして、hFE(Q1)/(hFE(Q1)+1)≒1の関係を使っています。
式(73)で表される、VINが減少中にQ1が飽和時領域から活性領域に移行する瞬間のVINを、VINAという定数で表す事にします。つまり、VINAは式(74)で定義されます。
VINが、式(74)で与えられるVINAよりも下がると、Q2が飽和領域にあるまま、Q1が飽和領域から活性領域に移行します。Q1が活性領域に移行した時に起こる事を考えます。
Q1が活性領域に移行すると、それまでVINの低下と共にVINと同じペースで低下してきたV1は、I1の減少と共に上昇を始めます。
参考:Q1が飽和領域にあった場合は、式(63)が成立していたので、VINが下がると、V1は、VINが下がったのと同じ電圧だけ下がっていました。
ここで、Q1が活性領域にある期間の、V1を求めます。
Q1が活性領域に移行してしまうので、図54の等価回路は使えなくなります。
しかし、当初はQ2が飽和領域にとどまるので、図53の等価回路は使い続けられます。
Q1が活性領域に移行しても、式(63)と同様、式(75)は成立し続けます。
よって、Q1が活性領域に移行しても、式(64)と同様に、式(76)は成立し続けます。
Q2は遮断領域にあるままで、Q1は活性領域に移行しているので、hFE(Q1)>>1を仮定すると、式(53)が成立します。
式(53)と式(76)より、I1は式(77)の様に求まります。
この式を式(24)に代入すると、V1は式(78)の様に求まります。
この様にV1が求まりました。
式(78)と式(75)より、Q2のベース-エミッタ間電圧V1-V2は、式(79)の様に求まります。
VINが下がると共に、Q2のベース-エミッタ間電圧V1-V2は、時間が経つにつれ上がります。そして、V1-V2が0.7Vに達すると、Q2が遮断領域から活性領域に移行します。
次に、Q2が活性領域に移行する時のVINを求めます。
前述の様に、Q2が活性領域に移行する時には、式(80)が成立しているはずです。
式(80)に式(79)を代入すれば、Q2が活性領域に移行する時のVINが、式(81)の様に求まります。
VINの電圧が式(81)の値まで下がると、Q2が遮断領域から活性領域に移行します。そうするとQ2の各端子に電流が流れ始めるため、図53の等価回路は使えなくなり、元々の回路(図48)に立ち返って考える必要が出てきます。
Q2が活性領域に移行すると、次の様な正帰還が掛かります。
この正帰還により、I5の増加とI2の減少が短時間に一気に進みます。
ただし、NPNトランジスタであるQ1の極性を考えると、I2は負の値にはなりませんから、I2=0になった時点で、正帰還のループは解消します。
I2=0になるという事は、Q1は遮断領域に移行するという事ですから、Q2の動作の解析は、図50の等価回路を使って行う事ができるようになります。
図50の回路において、Q2が活性領域にとどまるか、飽和領域に移行するかについては、5ページのコラムで説明しました。
結論だけをいうと、式(43)(近似的には式(42))が成立していれば、Q1が活性領域から遮断領域に移行する時に、Q2は活性領域から飽和領域に移行します。
式(43)が成立しない場合は、図48のシュミットトリガ回路の動作が不完全になるので、この回路は式(43)を満たす様に設計されているはずです。
この様にして、適切に設計されたシュミットトリガ回路の場合は、Q2が飽和領域に移行して、図50よりも単純な、図51の等価回路で回路の解析を行う事ができる様になります。
この時、出力電圧VOUTは式(29)で与えられるVLになります。
注:5ページで式(29)を導出した時は、VIN=0の場合でした。今はVINが高い電圧からVTHLにまで低下した時の話をしているので、前提条件が違うのですが、式(29)の導出過程を見ると、図51の等価回路を使っているため、同じ等価回路になる今回も、VOUTは同じ値になります。
直前までQ2が遮断領域にあってVOUT=VCCだったので、VINが式(81)で表わされる値にまで下がった瞬間に、VOUTがVCCからVLに急落した事になります。つまり、VINが式(81)で表わされる値にまで下がった瞬間に、入力がLと認識される様になったのです。
この、入力電圧が降下中に入力がLと認識される様になる電圧をVTHLと定義すると、VTHLは、式(81)のVINをVTHLに書き換える事により、式(82)の様に表されます。
図48の回路定数と同じR1=100[kΩ]、R2=3.3[kΩ]、VCC=5[V]を代入すると、VTHL≒0.837[V]が得られます。
このシュミットトリガ回路のヒステリシス電圧VTLH−VTHLは、式(45)と式(82)を代入する事より、式(83)の様に得られます。
なお、Q2が遮断領域から飽和領域へと移行すると、V2の値は式(31)に示した様に、VLになります。(式(31)の導出過程でも図51の等価回路を使っている事に注意)
入力電圧VINが低下中に、VTHL<VIN<VINAの範囲に入っている時は、Q1が活性領域にあって、Q2が遮断領域にあるという、ちょっと特殊な状態になる事を説明しました。この状態以外では、Q1が遮断領域にあってQ2が飽和領域あるか(入力がLと認識されている状態)、Q1が飽和領域にあってQ2が遮断領域にあるか(入力がHと認識されていて、かつ、VIN≧VINAの状態)のどちらかです。
NPNトランジスタをスイッチとしてとらえると、遮断領域にある場合はOFFになっている状態で、飽和領域にある場合はONになっている状態だといえます。
入力電圧がVTLHを超えて上昇する際には、正帰還の働きにより、Q1は速やかに遮断領域から飽和領域へ移行し、Q2は速やかに飽和領域から遮断領域に移行しますので、Q1にせよ、Q2にせよ、活性状態にある時間は、非常に短時間(トランジスタをスイッチング動作させる場合のスイッチング時間程度)です。
入力電圧がVTHLを超えて低下する際には、やはり正帰還の働きにより、Q2は速やかに遮断領域から飽和領域に移行しますので、Q2が活性領域にある時間は、非常に短時間です。
トランジスタがONでもOFFでもない活性領域に、ある程度の時間とどまるのは、入力電圧VINが低下時にVTHL<VIN<VINAが成立している場合のQ1だけなのです。
この様に、図48のシュミットトリガ回路では、Q1もQ2も、基本的にスイッチング動作(活性状態にとどまる事なく、OFF状態である遮断領域とON状態である飽和領域の間を行き来する動作)をするのですが、入力電圧VINが低下時にVTHL<VIN<VINAが成立している場合のQ1だけが例外になります。
とはいえ、普通の設計条件では、VTHLとVINAは非常に近い電圧になりますので、この例外状態は、非常に狭い電圧の範囲で生じるだけです。
例えば、図48の回路定数と同じR1=100[kΩ]、R2=3.3[kΩ]、VCC=5[V]の条件で計算すると、VTHLは0.982VでVINAは1.028Vと、差は0.046Vしかありません。
とはいえ、この狭い領域で生じる特殊な状態について、少し補足しておきます。
Q1が活性領域で、Q2が遮断領域にある事から、図53の等価回路を使って、Q1の動作解析をする事にします。
この等価回路において、Q1のコレクタ電流I2は、式(77)の通り求まります。この式(77)を式(49)に代入する事により、式(84)が得られます。
この式から、VINが1V低下する度にINは1hFE(Q1)R2[A]だけ減少する事が分かります。この事から、VINが低下時にVTHL<VIN<VINAが成立している場合の入力インピーダンスZINAは、式(85)の様に求まります。
このZINAは、ZINLの∞(式(48)参照)とZINHのR1//R2(式(68)参照)の間の値になります。
入力電圧がVINA以下になった事は、出力電圧VOUTからは判断できませんが、入力インピーダンスの上昇という形で、シュミットトリガ回路外部に影響を及ぼします。
VINがVTHLにまで下がって、Q1が飽和領域から遮断領域に移行し、Q2が遮断領域から飽和領域に移行すると、V2の値がVLになる事は先ほど説明しました。そしてこの時、図51の等価回路で回路の解析ができるのでした。
さらにVINが下がって、VIN<VTHLとなった場合は、Q1のベース電圧VINがさらに下がる一方で、Q1のエミッタ電圧V2はVLのままになるので、Q1のベース-エミッタ間電圧VIN-V2はさらに低下します。そのため、Q1は遮断領域内にとどまり、図51の等価回路が成立し続け、Q2は飽和領域にとどまります。
参考:図51より、Q2が飽和領域内にとどまる限り、V2の値はVINの値に無関係に決まり、一定値(VL)になる事が分かります。
よって、入力電圧VINに関わらず出力電圧VOUTの値はVLで一定になります。
また、Q1が遮断領域にとどまるため、Q1のベース電流VINは流れず、入力インピーダンスは∞になります。
以上で、図48のシュミットトリガ回路の動作の解説が一通り終わりました。
次のページでは、図48の回路の動作の解析に必要な式をまとめます。
