「シュミットトリガ回路」の解説(8)

このページをスマホなどでご覧になる場合は、画面を横長にする方が読みやすくなります。

目次へ前のページへ (1) (2) (3) (4) (5) (6) (7) (8) (9) 次のページへ

2020年01月03日

更新

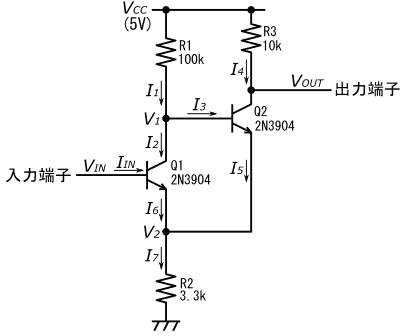
5ページの図48の、NPNトランジスタで構成した非反転型シュミットトリガ回路の動作について、引き続き解説します。

5-1-2-8.回路の動作のまとめ

これまで、図48に示すNPNトランジスタを用いた非反転型シュミットトリガ回路について、回路動作の解説を行ってきました。説明がとても長くなったので、ここで要点をまとめておきます。

↑ 画像をクリックすると拡大

図48(再掲)、NPNトランジスタで構成した非反転型シュミットトリガ回路

この回路の入出力電圧特性は、おおよそ図49の様になります。

↑ 画像をクリックすると拡大

図49(再掲)、図48の非反転型シュミットトリガ回路の入出力電圧特性

電源電圧VCC、抵抗R1の抵抗値R1、抵抗R2の抵抗値R2、および抵抗R3の抵抗値R3より、図48の回路の特性を表す各種の定数が、表5の様に求まります。

表5、図48のシュミットトリガ回路の特性を表す定数を求める式一覧
定数	意味	式
`VTLH`	入力がLからHに変わる時の閾値	`VTLH`≒`R2`(`R1`+`R3`)`R1R2`+`R2R3`+`R3R1VCC`+`R1`(`R2`+`R3`)`R1R2`+`R2R3`+`R3R1`・0.7[V] ・・・ (45)
`VTHL`	入力がHからLに変わる時の閾値	`VTHL`≒`R2R1`+`R2VCC`+`R1R1`+`R2`・0.7[V] ・・・ (82)
`VL`	出力がLの時の出力電圧	`VL`≒`R2`(`R1`+`R3`)`R1R2`+`R2R3`+`R3R1VCC`−`R2R3R1R2`+`R2R3`+`R3R1`・0.7[V] ・・・ (29)
`VH`	出力がHの時の出力電圧	`VH`=`VCC` ・・・ (52)
`ZINL`	入力がLの時の入力インピーダンス	`ZINL`=∞ ・・・ (48)
`ZINH`	入力がHの時の入力インピーダンス (例外あり。下記の注を参照)	`ZINH`≒`R1R2R1`+`R2`=`R1`//`R2` ・・・ (68)

注:出力がHの場合でも、入力電圧VINがVTHL<VIN<VINAの範囲に入っている時は、出力インピーダンスがZINAになります。詳しくは前のページのコラムをご覧ください。また、VINAの値については式(74)を、ZINAの値については式(85)をご覧ください。

また、R1～R3、およびVCCは、表6に示す3つの制約条件を満たしている必要があります。

表6、`R1`～`R3`および`VCC`が満たすべき制約条件
番号	制約条件
1	`R1`≦`hFE(Q2)R3`−`hFE(Q2)`(`R2`+`R3`)0.7[V]`VCC` ・・・ (43) (下記の注を参照の事)
2	`R2`<`VCC`0.7[V]−1`R3` ・・・ (47)
3	`R1`≧12+14+`VCC`0.7[V]·`R2R3`0.7[V]`VCC`·`R3` ・・・ (61)

注:hFE(Q2)は、トランジスタQ2のhFE(エミッタ接地電流増幅率)です。hFEはトランジスタの型番、個体差、温度、コレクタ電流などによって影響を受けますので、トランジスタのデータシートに載っている値よりかなり小さめに見積もって計算する方が無難です。hFE(Q2)をかなり小さめに見積もる前提なら、式(42)の簡易的な式で代用できます。また、R1≦10R3と設定すると、ほとんどの小信号トランジスタで動作する様になりますので、トランジスタのデータシートをチェックする必要がなくなります。

R1≦hFE(Q2)R3 ・・・ (42)

5-1-3.回路の動作の解析例

図48のシュミットトリガ回路において、表5の数式に回路定数(VCCとR1～R3)を代入して計算する事で、シュミットトリガ回路の特性を表す各定数が求まる様になりましたので、実際にシュミットトリガ回路の特性を計算してみましょう。

5-1-3-1.表5の数式よる各定数の計算と表6の数式による制約条件のチェック

例として、図48の回路定数(VCC=5[V]、R1=100[kΩ]R2=3.3[kΩ]、およびR3=10[kΩ])と表5の各式に代入すると、各定数は表7の様に求まります。

表7、図48の回路定数を表5に代入して求めた各定数
定数の記号	値
`VTLH`	2.015V
`VTHL`	0.837V
`VL`	1.315V
`VH`	5.000V
`ZINL`	∞Ω
`ZINH`	3.19kΩ

注:表7にはVTLH、VTHL、VL、およびVHの値が、1mV(0.001V)の桁まで書いてありますが、表5の数式でmVオーダーまで正確に計算できるという訳ではありません。表7の値は、後述する様に、LTSpiceのシミュレーション結果と、0.1～0.2V程度の差が出るのを確認しています。1mVの桁まで記載したのは、表5の式を読者が検算する際に便利だと、筆者が思ったからです。表5の数式は、いわゆる0.7V近似や、hFE>>1や、VCE(SAT)=0の近似を用いて計算した式なので、完全に現実の現象と一致する式ではありません。大まかな計算はこれらの式でできますが、より精密には、LTSpiceなどの回路シミュレータを用いたり、実際に回路を組み立てて測定するなど、別の手段が必要です。

また、図48の回路定数(VCC=5[V]、R2=3.3[kΩ]、およびR3=10[kΩ])と、2N3904のデータシートで調べたhFEの最小値であるhFE(Q2)=30を、表6の各制約条件を求める不等式の右辺に代入すると、表8の様な制約条件が出てきます。

表8、図48の回路定数と`hFE(Q2)`=30から求めた制約条件
番号	制約条件
1	`R1`≦244[kΩ]
2	`R2`<61.4[kΩ]
3	`R1`≧2.96[kΩ]

図48の回路定数は、表7の制約条件を満たしています。(表7の制約条件を満たしていない場合は、図48の回路がうまく動作しない可能性があります)

なお、他の回路定数のシュミットトリガ回路についても解析してみたいと思われる方は、表5と表6の計算式を組み込んだExcelのワークシートを使うと便利です。(図55参照)

参考:バイポーラトランジスタを用いたシュミットトリガ回路の動作解析・設計サービスという、オンラインでバイポーラトランジスタを使ったシュミットトリガ回路の動作解析や設計ができるサービスも始めました。こちらも、ぜひご利用ください。

図55、シュミットトリガ回路の特性を解析するためのExcelのワークシート

このワークシートは、以下のリンクからダウンロードできます。Excel2013で作成したので、それ以降のExcelでは問題なく使えるはずです。

シュミットトリガ解析用Excelワークシートのダウンロード ana-schmitt.xlsx (25kB)

ワークシートをダウンロードしたら、ピンク色のセルに、色々な数字を入れてみてください。

参考:ピンク色のセル以外は、保護して、値を書き換えられない様にしてあります。

例えば、VCC=8[V]、R1=12[kΩ]、R2=4.7[kΩ]、R3=10[kΩ]の条件で解析すると、図56の様な解析結果になるはずです。

図56、VCC=8[V]、R1=12[kΩ]、R2=4.7[kΩ]、R3=10[kΩ]の条件で解析した例

図56の下の方に、R1≦261.4[kΩ]という制約条件が表示されていますが、R1を300kΩにして、意図的に制約条件を満たさない様にすると、図57の様な解析結果になります。

図57、R1を300kΩにして意図的に制約条件を満たさない様にして解析した例

R1の値を入力した直後に、その値が赤い太字で表示される様になります。この赤い太字は、制約条件を満たしていない事への警告です。

また、図57の下の方にも、R1≦261.4[kΩ]の制約条件が守られていない事を示すNGの表示が出ています。

この様に、制約条件を満たしておらず、シュミットトリガ回路が正常に動作しない可能性がある場合は、警告を出して注意を促す様になっています。

5-1-3-2.表5の式による解析結果のLTspiceによる検証

表5および表6の式と、それらの式を組み込んだExcelのワークシートにより、図48のシュミットトリガ回路の回路定数を色々変えた場合に、どの様に特性が変わるかを気軽に求める事ができる様にはなりましたが、これらの式がどの程度の精度で成り立つのかが気になります。

というのも、表5の式を求める時に、活性領域または飽和領域のNPNトランジスタのVBEベース-エミッタ間電圧は0.7Vになるという近似(いわゆる0.7V近似)を使ったり、hFE>>1の場合に近似的に成り立つhFEhFE+1≒1という式を使っていたり、VCE(SAT)≒0(VCE(SAT)はコレクタ-エミッタ間飽和電圧)という近似式を使っていたりと、あらゆるところで近似式を使っていました。当然、表5の計算結果には誤差が伴うはずです。

そこで、LTspiceで図48の回路を使ってシミュレーションし、表7の計算結果がどの程度の誤差を持っているか評価する事にしました。

シミュレーションに使ったファイルは、以下のリンクからダウンロードできます。

シュミットトリガ回路のLTspiceシミュレーション用ファイルのダウンロード schmitt.asc (2kB)

ダウンロードしたファイルをLTspiceで開くと、図58の様な回路図が出てきます。これは、図48の回路図を、図48に使われている2N3904というトランジスタを使い、抵抗値も図48の通りに設定して入力した回路です。

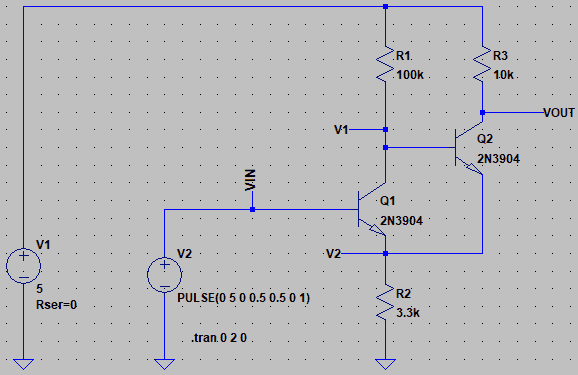
図58、ダウンロードしたファイルをLTspiceで開くと出てくる回路図

シミュレーションを走らせて、VINとVOUTの電圧をグラフに表示すると、図59の様になります。

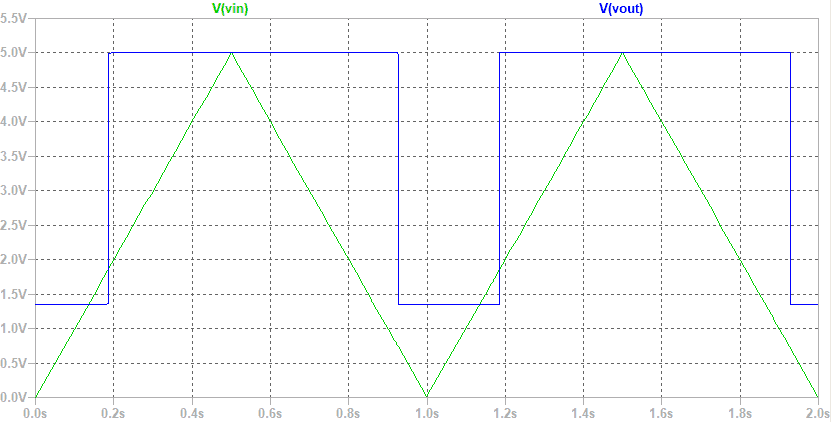
図59、図58の回路のシミュレーション結果の波形

VINには周波数1Hzで、最小電圧が0、最大電圧が5Vの三角波を入力しています。

ここで、VOUTが立ち上がっている部分の波形を拡大して表示させると、図60の様になります。

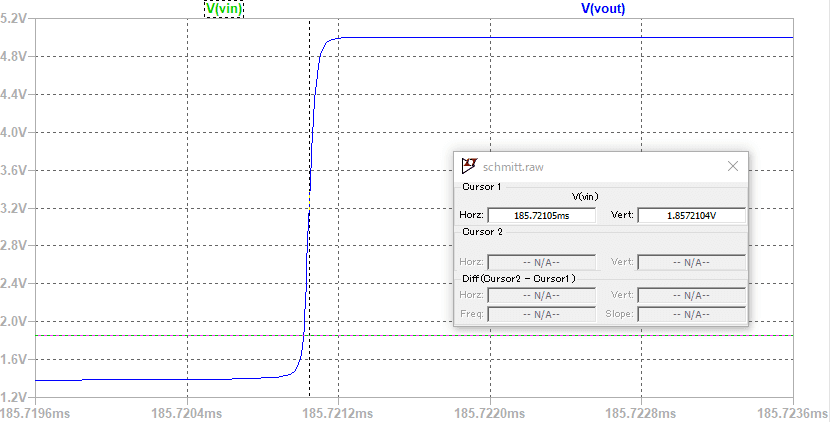
図60、VOUTが立ち上がっている部分の波形を拡大表示した様子

この状態でカーソル機能により、VOUTの立ち上がり時のVINを読み取ると、1.857Vという値が得られます。つまり、LTspiceのシミュレーションではVTLH=1.857[V]だったわけです。

同様に、VOUTが立ち下がっている部分の波形を拡大表示すると、VTHL=0.721[V]という値が得られました。

さらに、VINがちょうど0Vになるt=1[s](tは時刻)の部分の波形を拡大表示して、VOUTの値を値を読み取る事により、VL=1.345[V]という値が得られました。

表5の数式から計算した表7のVTLH、VTHL、およびVLの値と、LTspiceで得られた値とを比較したのが表9です。

表9、計算式で求めた`VTLH`、`VTHL`、および`VL`の値と、LTspiceのシミュレーションで求めたそれらの定数の比較
定数	表5の式から求めた値[V] (表7からの転載)	LTspiceのシミュレーションで求めた値[V]	誤差[V]
`VTLH`	2.015	1.857	0.158
`VTHL`	0.837	0.721	0.116
`VL`	1.315	1.345	−0.030

LTspiceのシミュレーションで得られた定数が正しい物として、表7の定数からシミュレーションにより得られた結果を引いた値を誤差として表示しています。

VTLHで0.158Vの誤差が出ていますが、この程度の誤差が問題にならない用途も多いと思います。

表5に載っている式には、2つのNPNトランジスタQ1とQ2の特性を表す定数(hFEなど)が全く入っていない事に注意してください。これらの式は、どんなNPNトランジスタを使うかを考えずに作った式なのです。

実際には、トランジスタによって、hFEやVBEやVCE(SAT)など、色々なパラメータが異なります。それらのパラメータのが異なる事により、シュミットトリガ回路の特性も微妙に異なります。

試しに、図48のシュミットトリガ回路のQ1とQ2を、2N3904と2SC2412Kと2SC4617EBの3種類のNPNトランジスタに換えて、LTspiceでVTLH、VTHL、およびVLを求めた値を表10にまとめました。

参考:2N3904、2SC2412K、2SC4617EBの3種類のNPNトランジスタは、いずれもコレクタ電流の定格値が150mA～200mAの範囲の小信号用トランジスタです。

表10、図48のシュミットトリガ回路のQ1とQ2の型番を換えて`VTLH`、`VTHL`、および`VL`をLTspiceのシミュレーションで求めた結果
記号	2N3904を使って求めた値[V]	2SC2412Kを使って求めた値[V]	2SC46176EBを使って求めた値[V]
`VTLH`	1.857	1.809	1.810
`VTHL`	0.721	0.673	0.673
`VL`	1.345	1.340	1.340

この様に、高々数十mVではありますが、トランジスタを換える事によって、VTLH、VTHL、VLの値が変化します。

よって、おおむねの値を計算するのには、表5や表6の数式を組み込んだExcelのワークシートを使うと便利ですが、厳密に値を求めるには、使用するトランジスタの型番を決めてから、LTspiceなどの回路シミュレータを用いる方がいいでしょう。

次のページでは、NPNトランジスタを用いたシュミットトリガ回路の設計法について解説します。