| 2019年03月19日 | 公開。 |
リング発振器(リングオシレータ)という、奇数個のインバータ(NOT回路)を使う発振回路があります。リング発振器の発振周波数は、インバータの動作速度が速いほど高くなるため、新しいタイプの論理デバイスが開発された場合に、その速度評価のために、リング発振器を作って、発振周波数を測る事が良くあります。
今回は、汎用ロジックICの74HC04のインバータ3個を使ってリング発振器を作成し、その動作を1Gspsの高速ロジアナにより観測しました。
リング発振器に関する詳しい説明は、用語集のリング発振器のページに載っているので、ここでは概略だけ説明します。
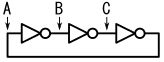
リング発振器は、奇数個のインバータを環状に接続して作る発振回路です。リング発振器を最も簡単に作るには、図1に示す様に、3個のインバータを環状に接続すると構成する事ができます。図1には、後の説明に使うため、各インバータの入力端子に、それぞれA点、B点、C点と名前を付けてあります。
図1のリング発振器の動作を考えてみましょう。インバータは二値論理回路(LかHの2種類の電圧のみを扱う論理回路)なので、ある時点のA点の電圧は、LまたはHのいずれかになります。
仮に、ある時点でA点の電圧がLと仮定して、その後の図1の回路の動作を考察してみます。(図2参照)
A点というのは、左のインバータの入力端子なので、同じインバータの出力端子であるB点の電圧は、A点の電圧を論理反転したHになるはずです。(図3参照)
B点というのは、真ん中のインバータの入力端子なので、同じインバータの出力端子であるC点の電圧は、B点の電圧を論理反転したLになるはずです。(図4参照)
C点というのは、右のインバータの入力端子なので、同じインバータの出力端子であるA点の電圧は、C点の電圧を論理反転したHになるはずです…と言いたいところですが、それだと最初にA点の電圧がLと仮定した事と矛盾してしまいます。(図5参照)
実際には、図5の様な矛盾は発生しません。というのは、インバータの出力電圧は、入力電圧が変化してからすぐに変化するわけではないからです。
インバータをはじめとする電子回路は、入力電圧が変化してから、出力変化が応答する(入力電圧の変化に応じて出力電圧が変化する)までにいくらかの時間がかかります。この様に、出力電圧の応答が入力電圧の変化に対して遅れる事を伝搬遅延といい、その遅れ時間の事を伝搬遅延時間といいます。伝搬遅延時間は、普通tpdと表記されます。
この伝搬遅延時間がある事により、図1において、回路のA点の電圧がLであるという信号がB点、C点と順に伝わり、再びA点に戻ってくるまでに、ある程度の時間が必要です。そして、再びA点に信号が戻ってくると、A点の電圧が上書きされるのです。(図6参照)
その後は、図7に示す様に、B点、C点、A点、B点…と、順に各点の電圧が上書きされ、変化していきます。
注:図2~図7では、最初にA点の電圧がLだと仮定しましたが、A点の電圧がHと仮定した場合は、全ての図でLとHが入れ替わります。A点の電圧をLと仮定するにせよ、Hと仮定するにせよ、いずれの場合もリング発振器は同じ周波数で発振します。
この電圧の変化をタイミングチャートで表すと、図8の様になります。
この様に、図1の回路は、A点、B点、C点ともに、周期6tpd、デューティ比50%の方形波で発振します。(tpdはインバータの伝搬遅延時間) また、3つの方形波の位相は120°ずつずれています。
また、リング発振器に使うインバータの数は、必ずしも3個でなくても構いません。3個以上の奇数(場合によっては1個でも可)であれば発振します。
N個(Nは奇数)のインバータを環状に接続したリング発振器の発振周波数fNは、式(1)により求まります。
この様に、インバータの数が多くなると、それに反比例して発振周波数が下がります。
リング発振器の発振周波数は、伝搬遅延時間tpdに反比例しますから、新しい種類の論理デバイス(デジタルIC)の開発をした時に、その論理デバイスのtpdを見積もるために、リング発振器を構成し、その発振周波数を測定する事が良くあります。
特に、高速の(tpdが小さい)論理デバイスを開発した場合は、tpdを直接、オシロスコープやロジックアナライザなどで測定しようとすると、時間分解能の高い、高価な測定器が必要になりますが、十分多くのインバータを環状に接続してリング発振器を構成すると、低い周波数で発振するため、時間分解能の比較的低い、安価な測定器で発振周波数を測定でき、式(1)を用いてtpdを計算により求める事ができます。
他にも、インバータのtpdが電源電圧に依存する事を利用すると、リング発振器は、制御電圧により発振周波数が制御できる発振器(VCO)として使えるなど、リング発振器は色々な応用ができる発振器として知られています。
次のページでは、74HC04を使って、実際にリング発振器を作ります。
